3 Interactions des mathématiques avec d’autres disciplines

Il faut donc se convaincre que toutes les sciences sont tellement liées ensemble, qu’il est plus facile de les apprendre toutes à la fois que d’en isoler une des autres. Si quelqu’un veut chercher sérieusement la vérité, il ne doit donc pas choisir l’étude de quelque science particulière : car elles sont toutes unies entre elles et dépendent les unes des autres…

           (Descartes, cité par Cunningham, 1989 : 78)

La représentation des objets et des phénomènes physiques par un discours mathématique abstrait, structuré et formalisé a fait des mathématiques un outil puissant et privilégié qui offrit aux sciences un essor prodigieux. Elles sont devenues ainsi un « langage » pour presque toutes les sciences. Autrement dit, les mathématiques ont permis d’introduire la mesure et la rigueur dans l’explication des phénomènes naturels dans diverses disciplines. Elles ont donné aux savants et savantes le moyen de prédire et de créer de nouvelles lois. La langue mathématique, de par son emploi, est connue et pratiquée des physicien·ne·s, des biologistes, des chimistes, des linguistes, des psychologues, des économistes… La biologie utilise les modèles mathématiques, le calcul des probabilités pour étudier la distribution statistique des caractères héréditaires dans la génétique mendélienne. La psychologie et la sociologie traduisent les résultats de leurs tests et enquêtes par des statistiques mathématiques. Les linguistes utilisent les modèles mathématiques pour décrire les langues et des outils mathématiques pour recueillir, enregistrer et classer les données.

Toutefois, cette influence des mathématiques dans les autres disciplines ne doit pas laisser croire que les mathématiques se suffisent à elles-mêmes et qu’elles ne sont pas pénétrées par les autres sciences. Le propos de Descartes que nous avons placé à l’ouverture de ce chapitre souligne effectivement l’existence des liens entre les savoirs. Si aujourd’hui l’approche encyclopédique a cédé la place à la disciplinarisation/parcellisation des sciences^[1], de plus en plus, des voix s’élèvent pour revendiquer la mise en place de « ponts » entre les disciplines, au nom de l’interdisciplinarité. Ces voix nous semblent en toute harmonie avec celle de l’UNESCO. Des propositions de Morin (1999), à la demande de cette institution, sont organisées en sept chapitres qu’il appelle « savoirs » et consignées dans son essai intitulé Les sept savoirs nécessaires à l’éducation du futur. Le deuxième chapitre de cet ouvrage, les principes d’une connaissance pertinente^[2], l’auteur recommande une approche transdisciplinaire ou polydisciplinaire nécessaire si l’on veut aider les apprenant·e·s à saisir les problèmes contemporains dans toute leur globalité et leur complexité; bref une approche qui permet de saisir « ce qui est tissé ensemble. » (Morin, 1999 : 19)

Dans cette volonté, et s’agissant du domaine de l’éducation spécifiquement, la question du rapport entre l’apprentissage scolaire et l’apprentissage dans la vie s’est posée de façon accrue.

Apprendre la vie, ce n’est pas apprendre comme on le fait à l’école. Ce qui distingue l’école et « la vie », c’est aussi la nature de cette activité que l’on nomme apprendre. À l’école, apprendre c’est écouter le professeur et retenir ce qu’il a expliqué – parfois, le regarder et retenir ce qu’il a montré. Apprendre par la vie, dans la vie, c’est en faire l’expérience ou l’observer, et réfléchir. (Charlot, cité par Niclot & Aroq, 2006 : 1)

L’enfant baigne donc dans un milieu fait de savoirs de différents ordres, mais qui sont liés et font sens. Aussi, créer des passerelles entre les disciplines scolaires, c’est rapprocher l’apprentissage scolaire de l’apprentissage de la vie. La question fondamentale, selon Méride Cidalise-Montaise, est : « en quoi certaines situations pédagogiques peuvent-elles faire contrepoids aux effets de la parcellisation institutionnalisée des savoirs sur l’élève? » (2015 : 53). La réponse à une telle question ne saurait venir de chaque discipline scolaire prise individuellement, mais davantage d’une prise en compte, de manière conjointe, des points d’intersection entre les différentes disciplines. Si une telle réflexion a été menée, puis des expérimentations faites, dans certains continents, elle reste encore peu discutée dans les écoles africaines. Au Kamerun par exemple, les nouveaux programmes scolaires de 2013 sont certes regroupés en six domaines d’apprentissage, mais la connexion entre les différentes matières manque :

Un domaine d’apprentissage pour sa part a pour fonction principale d’intégrer un ensemble de programmes d’études présentant des affinités afin de décloisonner les matières scolaires et de favoriser l’interdisciplinarité nécessaire au développement de nombreuses compétences effectives. (MINESEC, 2012 : 4)

Ces nouveaux curriculums s’intéressent plus à l’approche pédagogique basée sur les compétences avec entrée par les situations de vie qu’au décloisonnement des disciplines scolaires et à la notion d’« interdisciplinarité ». Les enseignant·e·s sont sensibilisé·e·s lors des séminaires qui, malheureusement, vont rarement plus loin que la lecture des programmes officiels et son application. On ne dispose pas de propositions fortes et concrètes visant à implémenter cette interdisciplinarité^[3] qui s’impose à nous, au fil de l’évolution du monde.

L’interdisciplinarité est, en effet, une question essentielle dans la réflexion contemporaine sur l’utilité sociale des savoirs scolaires. La compréhension par les élèves du monde dans lequel ils vivent, caractérisé par l’émergence d’une société du savoir et par une complexité croissante, s’accommode mal d’une appréhension par les disciplines cloisonnées qui souvent s’ignorent. (Niclot & Aroq, 2006)

L’interdisciplinarité dont nous parlons ici est dite interdisciplinarité scolaire. Elle se distingue, comme le soulignent Lenoir & Sauvé (1998), de l’interdisciplinarité scientifique^[4]. Elle se conçoit comme « la mise en relation de deux ou de plusieurs disciplines scolaires qui s’exercent à la fois sur les plans curriculaire, didactique et pédagogique et qui conduit à l’établissement des liens de complémentarité ou de coopération. » (Lenoir & Sauvé, 1998 : 12).

En fait, la réflexion sur les relations entre les disciplines a conduit à la mise en place d’un certain nombre de concepts dont il convient de préciser le sens. Suivant Lenoir et Hasni (2015), on distingue la monodisciplinarité qui désigne le recours à une seule discipline, la multidisciplinarité qui est le fait de recourir à deux ou plusieurs disciplines sans en préciser les relations, la pluridisciplinarité qui est une juxtaposition de deux ou plusieurs disciplines, et enfin, l’interdisciplinarité, « expression générique pour désigner toutes les formes de liens qui peuvent se dessiner entre les disciplines »^[5] (2015 : 13). Cette dernière comporte une forme particulière qui est l’intradisciplinarité, renvoyant aux interactions qui se font à l’intérieur d’un même champ disciplinaire.

Sur le terrain, nous pensons que la mise en place effective de l’approche interdisciplinaire au sein d’un établissement nécessite une réorganisation synchronique à la fois administrative et pédagogique des activités. Au-delà des actions individuelles que mènera chaque enseignant·e pendant ses séances de cours, il faudrait, pour les disciplines convoquées :

• fédérer les actions des élèves au sein des clubs et celles des enseignant·e·s au sein des conseils d’enseignement et des chantiers d’innovations pédagogiques pour mieux voir les liens;

• mener conjointement les activités monodisciplinaires (isolées dans le cadre d’une discipline) et les activités interdisciplinaires (en groupe avec d’autres disciplines);
• fixer des plages horaires hebdomadaires et d’activités pour la mutualisation ou mise en commun des ressources et des résultats des travaux monodisciplinaires;
• prévoir une journée ou une semaine d’interdisciplinarité scolaire qui, comme les autres journées (nationale ou internationale)^[6], sera célébrée à l’échelle des classes, des filières ou même des établissements. À cette occasion, la promotion de l’approche interdisciplinaire scolaire sera renforcée et les résultats obtenus par les compétences mobilisées seront présentés aussi bien à l’administration scolaire qu’au grand public;
• adopter éventuellement une bonification en termes de note de classe pour les apprenant·e·s en cours de scolarité. Cet aspect représente un enjeu important.

Il est vrai que ces réaménagements, qui en amont devraient bénéficier de l’aval des pouvoirs publics compétents, affecteront aussi bien les programmes d’enseignement que de la vie scolaire.

Pour le cas de cinq champs disciplinaires relevant de notre choix et incluant les trois catégories de notre sériation, nous proposons de visualiser les différentes conceptualisations à travers le schéma suivant :

Figure 4 : Conceptualisation des liens dans un contexte polydisciplinaire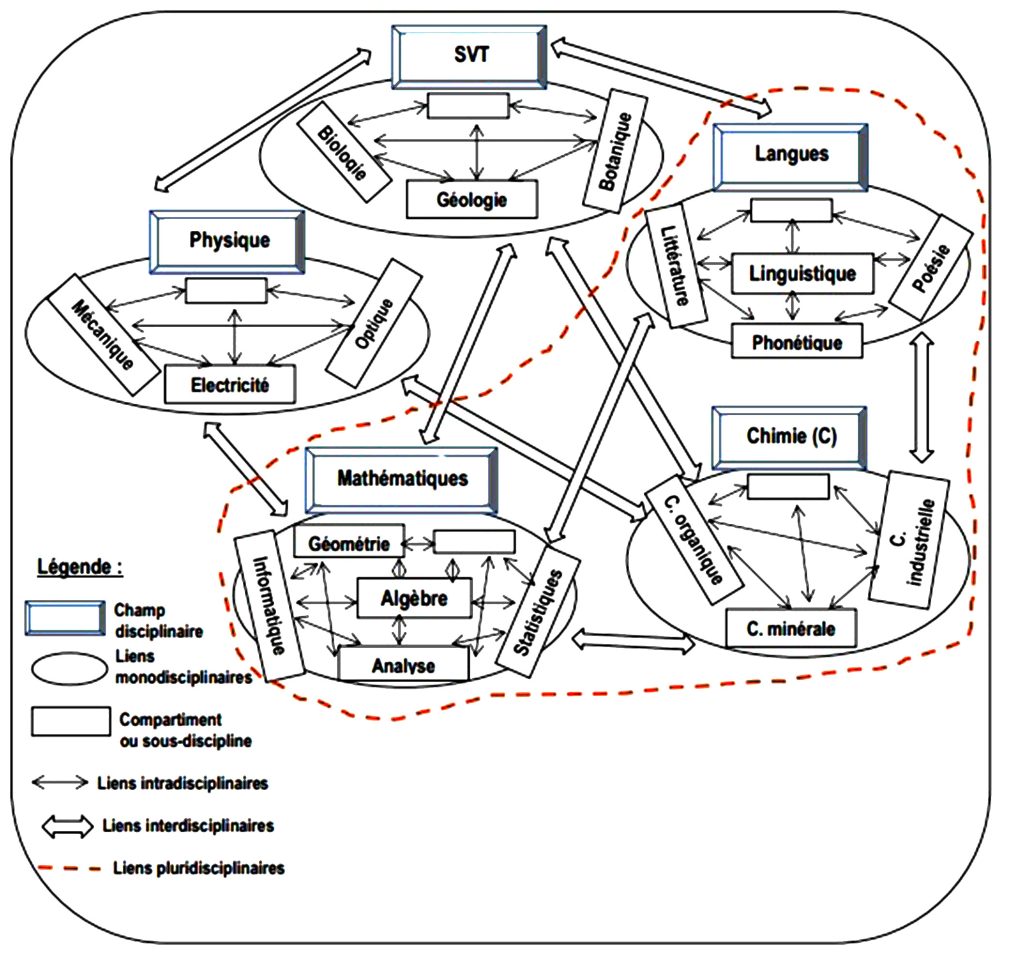

Sans toutefois répondre explicitement au problème d’opérationnalisation de cette interdisciplinarité dans la recherche et l’enseignement, en faisant ressortir notamment les modalités pratiques et les entraves, nous présentons de façon synoptique le principe et le processus d’interactions des mathématiques avec les autres disciplines.

Principe et processus d’interactions des mathématiques avec d’autres disciplines

La recherche en mathématiques a actuellement atteint un niveau incroyablement élevé pour le commun des humains que la diversité des résultats obtenus, les théories, les concepts. Bref, le vocabulaire mathématique a fait l’objet de dictionnaires issus de différentes collections. L’Encyclopædia Universalis « se veut ainsi le reflet du foisonnement et de l’enchevêtrement de diverses disciplines mathématiques » (Dictionnaire des mathématiques, 1997 : 8). La notion d’interdisciplinarité est vivante dans le domaine des mathématiques. « Comme le soulignait souvent Jean Dieudonné, c’est cette interdisciplinarité interne qui fait la force et l’originalité des mathématiques contemporaines. » (Dictionnaire des mathématiques, 1997 : 8). Dans leur développement, les mathématiques se sont ouvertes aux autres disciplines à travers des interactions dont le mode opératoire et le mécanisme fonctionnel sont singuliers pour chaque domaine (Greenwald & Thomley, 2012).

Principe d’adaptation du modèle mathématique avec le monde réel

Des interactions existent entre les ramifications des différentes branches des mathématiques et entre les mathématiques et les autres disciplines. Dans le second cas de figure qui est plus observable aujourd’hui, les chercheur·e·s travaillant dans les autres disciplines étudient ce que Descartes appelle le « monde réel »; celui-ci, par essence, est opposé au monde mathématique qui, lui, est intelligible et est fait majoritairement de notions abstraites comme les angles, les fonctions, les points, les nombres… Hurley (1980 : 493-495) consacre quelques pages aux interactions entre les mathématiques et les autres disciplines. Selon lui, les chercheur·e·s désirent établir, dans leur domaine de travail, des lois qui puissent expliquer ou régir les informations et les données qu’ils récoltent lors de leurs travaux, réalisés dans le monde réel. De telles lois prennent la forme d’énoncés mathématiques (équations, théorèmes, formules, propriétés, règles) relativement à un modèle mathématique conséquent avec des paramètres reflétant, dans la mesure du possible, le phénomène réel étudié : son mécanisme de fonctionnement, sa dynamique dans l’espace et dans le temps, entre autres. Ce modèle est souvent un système mathématique abstrait contenant, autant que faire se peut, toutes les variables essentielles existant dans l’arrière-plan (Hurley, 1980).

Ensuite, par un travail purement mathématique sur ce modèle, les mathématiciens et les mathématiciennes peuvent obtenir des résultats à condition qu’ils/elles disposent des outils adéquats pour y parvenir. L’interprétation de ces résultats, dans le monde réel, peut permettre de faire des prédictions sur le comportement ultérieur du phénomène. La comparaison de ces prémonitions avec les résultats empiriques permet de mesurer alors le degré avec lequel le modèle mathématique capte l’essence de la situation réelle du phénomène étudié. Selon Hurley (1980), deux cas de figure se présentent :

Si les prédictions correspondent presque parfaitement aux résultats expérimentaux, alors le modèle sera adopté et ses résultats seront appelés lois^[7] du champ externe. Si les prévisions sont faiblement corrélées avec les résultats expérimentaux, alors un modèle révisé ou affiné peut être construit, sous réserve peut-être d’être encore affiné après une nouvelle expérimentation^[8]. (Hurley, 1980 : 394)

Ainsi, si les résultats prévisionnels sont en corrélation parfaite avec les résultats expérimentaux, alors ce modèle mathématique sera adopté par les chercheurs et les chercheuses de la discipline concernée. Dans le cas où la corrélation entre les deux types de résultats est faible, un autre modèle plus élaboré et plus fin doit être construit en multipliant davantage les expériences.

Hurley (1980) résume les deux situations à travers le schéma ci-après.

Figure 5 : Processus d’adaptation du modèle mathématique avec le monde réel selon Hurley

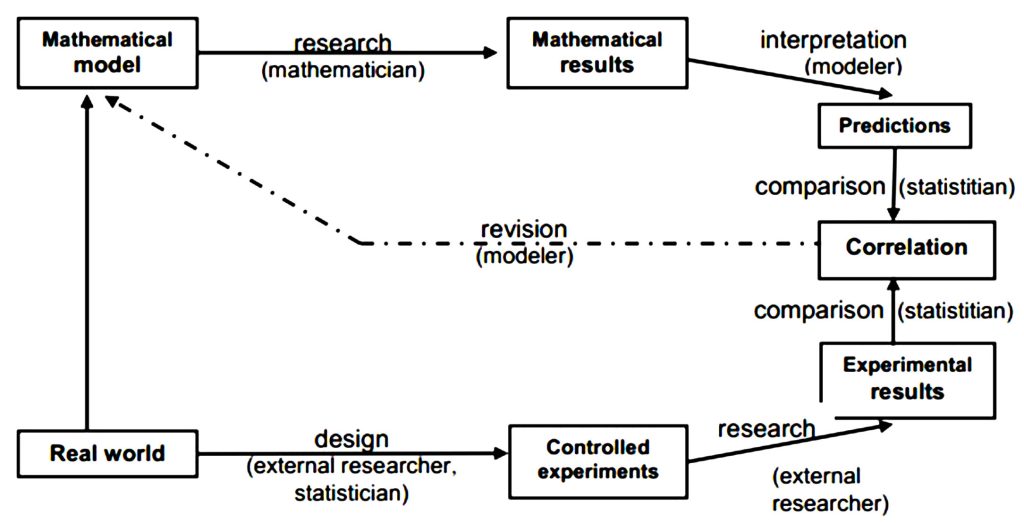
Cette représentation schématique présente un intérêt capital pour la MCA dans la mesure où elle établit des liens solides entre le modèle mathématique et le monde réel. Cependant, un aspect semble être écarté par Hurley. L’idée qu’une faible adéquation entre les résultats du modèle et la réalité peut conduire à une compréhension erronée selon laquelle l’élaboration et la prolifération des théories se font de manière isolée. Or, il faut appréhender ces relations en termes de perfectionnement, d’amélioration, d’effacement des « lacunes » du modèle (Khun, 1972). Nous pensons donc qu’il faut insister sur les liens, les filiations épistémologiques entre différents théories et modèles. Sans cet aspect, on perdrait une part importante d’informations sur la construction des connaissances et le développement cognitif : les savoirs mathématiques ne naissent pas d’eux-mêmes, ce sont des constructions de l’esprit humain. Il convient également de présenter avec précision les éléments qui entrent en jeu dans les interactions, notamment le monde réel, dans lequel les observations du phénomène étudié sont faites, et le modèle mathématique, qui relève du monde intelligible. Le modèle mathématique étant construit à partir des informations issues du phénomène du monde réel, il serait plus intéressant de disposer en interaction, d’une part, les deux ensembles (monde réel et monde intelligible); et d’autre part, les objets appartenant à chacun des deux ensembles (phénomène réel et modèle mathématique). De plus, le schéma de Hurley (1980) nous laisse visiblement dans une impasse lorsqu’il y a corrélation parfaite entre les prédictions et les résultats expérimentaux. Il serait important d’indiquer un emplacement (cadre) qui montre le résultat (modèle) final qui fera office de loi dans le domaine réel. Il convient de remarquer qu’ici, le développement des modèles mathématiques a créé un meilleur cadre de réflexion qui, à son tour, a permis la synthétisation des lois, leur regroupement et la trouvaille d’une certaine unité entre elles.

Par ailleurs, l’inadéquation entre le modèle mathématique et le monde réel ne se résout pas toujours par l’édification de nouveaux modèles mathématiques. En effet, on peut partir de la mise en pratique des paramètres du modèle en réexaminant leur fonctionnement dans le monde réel. Le cheminement pourrait donc être représenté sous la forme d’une bifurcation qui a pour point de départ le monde réel, puis l’élaboration du modèle mathématique, suivie des résultats obtenus; arrivée à ce niveau, deux chemins se fraient : soit le retour vers le modèle (Hurley, 1980), soit le retour au monde réel. Notre proposition consiste à considérer prioritairement ce dernier chemin. De manière concrète, en recourant à ce chemin, cela nous permet de résoudre des problèmes tels que la mauvaise formulation d’un problème, l’omission d’un paramètre, etc.

En reprenant les grands traits du schéma de Hurley, nous proposons ci-dessous une configuration enrichie de nos propres expériences.

Figure 6 : Processus enrichi d’interactions des mathématiques avec d’autres disciplines

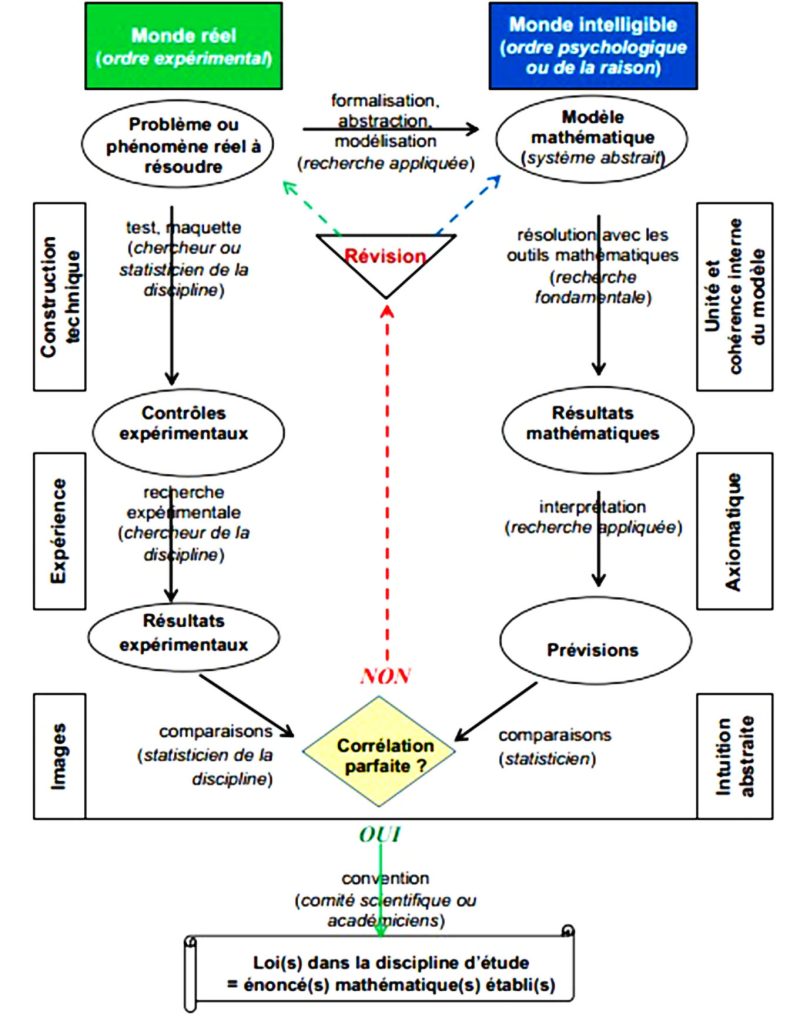
Ce schéma montre que le mécanisme interactionnel est fait d’actions bien planifiées aussi bien dans le monde réel que dans le monde intelligible. Dans le monde réel, on commence par des constructions techniques à travers des tests, puis l’expérience à l’aide des protocoles contrôlés débouchant sur des résultats expérimentaux, et enfin, l’image se crée à travers les comparaisons. Tandis que dans le monde intelligible, on commence par assurer la cohérence et l’unité interne du modèle, puis l’axiomatique aboutit aux prédictions et l’intuition permet de discerner ces prédictions.

Mais il peut arriver que le mathématicien ou la mathématicienne trouve plusieurs modèles relatifs à un même phénomène réel. Le choix du meilleur modèle devient alors crucial. Chaque modèle donne des prédictions sur le comportement du phénomène et nous pouvons nous demander lequel des ensembles de prévisions correspond le mieux à l’expérience menée. Dans certains cas, tel modèle est parfaitement adéquat. Dans d’autres, un autre modèle est préférable. Ainsi, le choix du modèle à utiliser ne dépend plus seulement des facteurs mathématiques, mais également des facteurs environnementaux; bref, des facteurs extérieurs ayant directement des effets sur le phénomène réel étudié.

Processus d’interactions des mathématiques avec d’autres disciplines

En nous inspirant du schéma du processus d’adaptation du modèle mathématique dans les autres disciplines élaboré par Hurley (1980 : 494) et des travaux de Wieruszewski (1994), nous proposons la schématisation suivante, qui à la fois simplifie le processus pour les apprenant·e·s du secondaire tout en l’enrichissant par l’ajout d’opérations à mettre en place.

Figure 7 : Processus d’interactions entre langue courante et métalangue mathématique

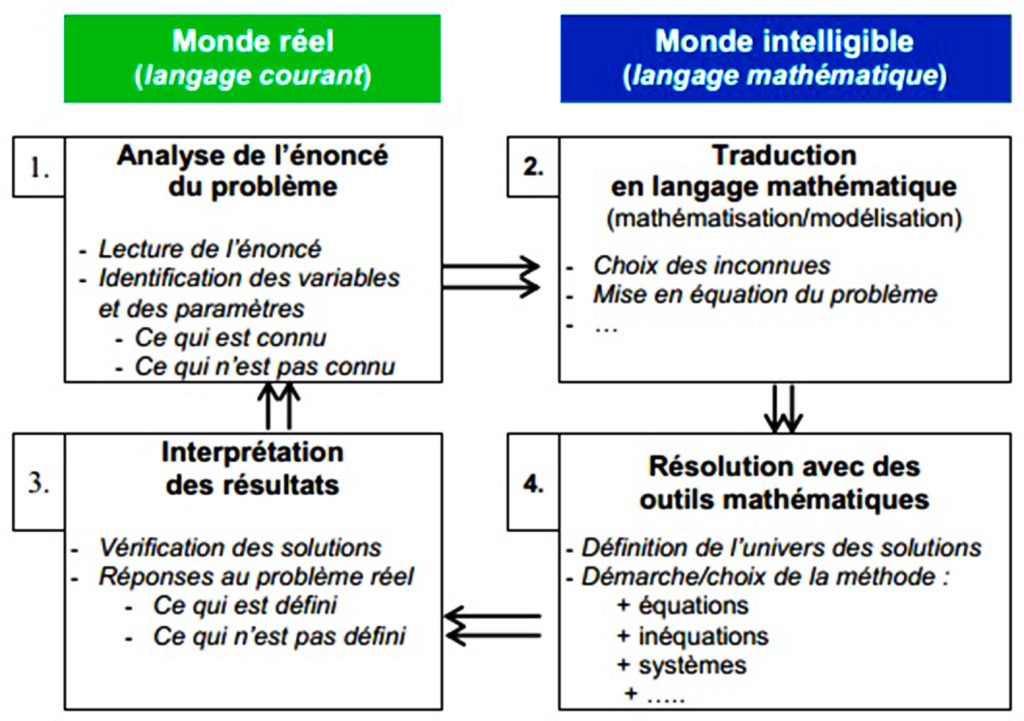
Le problème réel est d’ordinaire posé dans la langue courante et dans des situations de communication quotidienne. Le problème exprimé en dehors du raisonnement formel semble dépouillé d’un ensemble de contraintes et d’éléments sous-jacents : les non-dits, les implicites, les sous-entendus qui engendrent nécessairement des erreurs et des malentendus^[9]. Il se traduit ensuite en langue mathématique qui doit établir des lois ou des règles permettant de décrire explicitement des faits observables et identifiables. Cette langue qui se différencie des langues naturelles tend donc à effacer certains paramètres susceptibles de connaitre des variations, notamment les paramètres du contexte d’énonciation : le sujet parlant, ses sentiments, le temps, l’espace^[10]. Ensuite, le problème est résolu selon les méthodes et techniques spécifiques. Enfin, les résultats éventuels trouvés sont vérifiés et réinterprétés en langue naturelle.

À titre d’illustration, nous présentons dans le tableau ci-dessous des exemples de rapports analogiques simples qu’on pourrait faire entre une vision philosophique et une vision mathématique de quelques formulations de sujet dans des domaines de recherche ou de travail donnés.

Tableau 9 : Exemples de rapports analogiques simples entre une vision philosophique et une vision mathématique de quelques formulations de sujet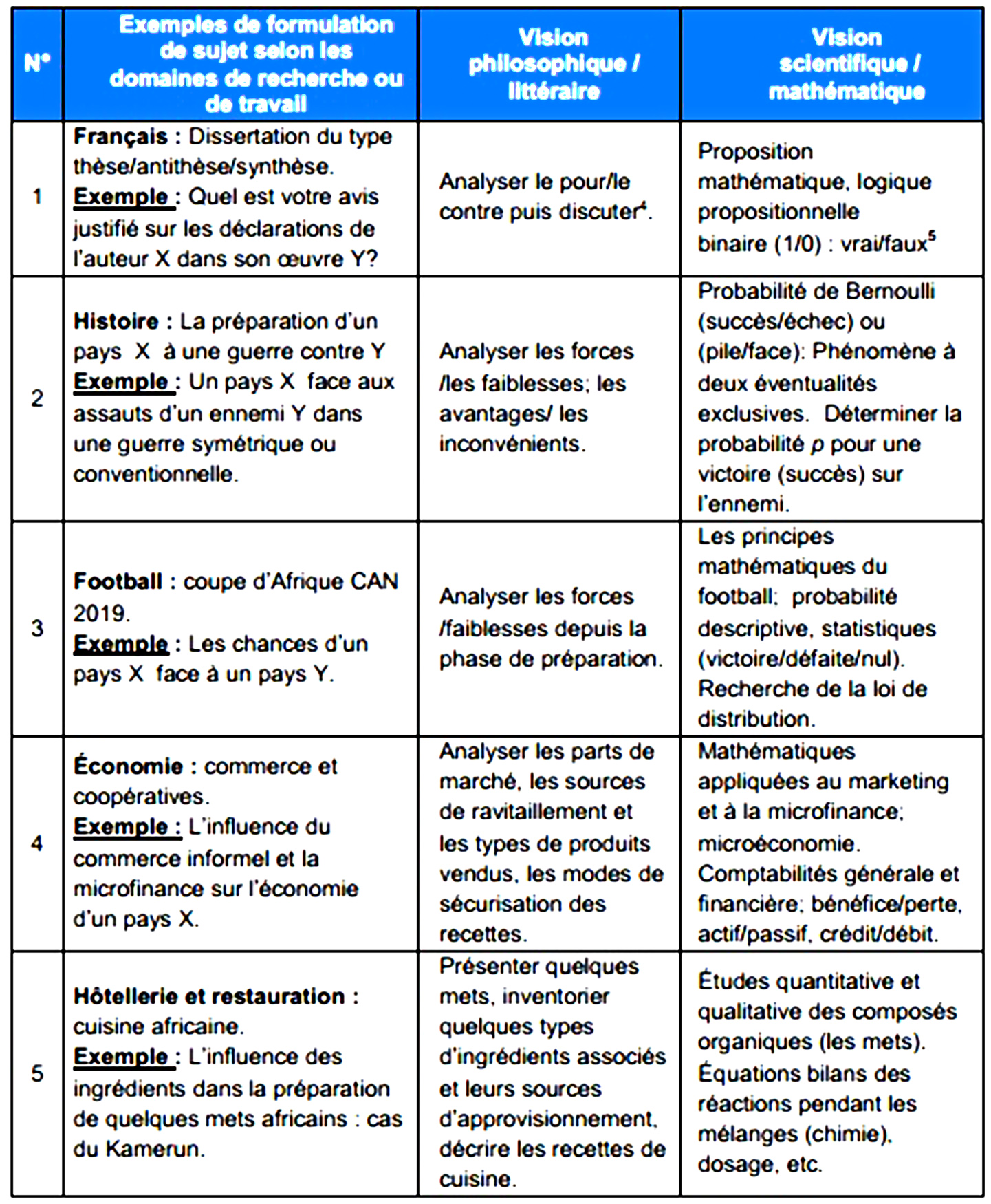

Ce tableau fait ressortir deux manières d’envisager les problèmes et de les résoudre. Il met aussi en évidence les relations entre les mathématiques et les études littéraires. Ceci constitue l’un des enjeux de la MCA qui ambitionne d’appréhender l’apprentissage des mathématiques en corrélation avec les activités humaines. Les exemples foisonnent dans divers secteurs.

Nous rappelons que les mathématiques appliquées traitent du monde réel où les critères absolus (vrai/faux, un/zéro…) qui relèvent des mathématiques fondamentales et notamment de la logique formelle, classique, binaire ou booléenne ne sont plus tout à fait appropriés. Très souvent, aucun modèle n’est absolument correct. Dès lors, il devient plutôt intéressant de savoir et faire savoir lequel parmi les modèles proposés donne la meilleure approximation du comportement observé pendant l’expérience. En outre, les critères deviennent relatifs, de l’ordre de la logique plurivalente ou logique floue (Godjevac, 1999) d’autant plus que dans la réalité humaine, la notion de vérité est plus aléatoire. La logique floue est en effet une extension de la logique classique qui permet alors de modéliser et de simuler des complexités des données de la réalité humaine. Elle se rapproche, dans une certaine mesure, de la flexibilité du raisonnement humain. Elle permet de traiter des variables non exactes dont la valeur peut varier entre 0 et 1. Ses applications sont nombreuses, allant des systèmes de jeux vidéo aux pilotes automatiques en passant par les microondes, la décision du montant du pourboire à l’issue d’un repas au restaurant en fonction de la qualité ressentie du service ou de la qualité de la nourriture (Kono, 2014). Il faut souligner que le problème ne se pose pas seulement en termes de modélisation, mais aussi en termes de simulation de temps de calcul. À ce propos, on pourrait par exemple questionner la qualité d’un modèle métrologique qui ferait des prédictions sur deux jours alors que les calculs en machine prendraient trois jours.

À l’observation, toutes ces expériences montrent l’étendue des relations réciproques qu’entretiennent les mathématiques avec les autres disciplines; des corrélations aussi nombreuses que diverses existent, comme le montrent les exemples que nous allons examiner.

Les mathématiques se révèlent véritablement aujourd’hui comme une science de services, c’est-à-dire une science qui met ses outils à la disposition des autres disciplines. Pourtant, Von Neumann fait observer que la dimension utilitaire des travaux mathématiques n’est pas toujours perceptible immédiatement.

Des exemples illustratifs d’interactions des mathématiques avec d’autres disciplines

Dans l’ensemble, il est uniformément vrai en mathématiques qu’il y a un laps de temps entre une découverte mathématique et le moment où celle-ci est appliquée, que ce laps de temps peut aller de 30 à 100 ans, et encore plus dans certains cas et que tout le système semble fonctionner sans aucune direction, sans aucune référence à l’utilité, et sans aucun désir de faire des choses qui sont utiles^[11]. (Von Neumann, cité par Bródy & Vámos, 1995 : 652)

En d’autres termes, l’utilité des découvertes en mathématiques se mesure presque toujours a posteriori, des années après leur formulation. Cela ne devra pas laisser croire que les mathématiques sont inutiles pour autant. Les mathématiques sont utiles pour elles-mêmes, à travers l’intradisciplinarité; et pour diverses autres disciplines d’enseignement qui se prêtent de quelque manière que ce soit à des liens interdisciplinaires avec elles; dans le cadre de l’interdisciplinarité, à l’effet de justifier, de valider ou de soutenir l’homologation de certains de leurs principes et lois. Une raison évidente pour laquelle nous pensons que l’importance d’une science se juge également dans sa capacité à interagir avec les autres disciplines.

Regroupement des disciplines scientifiques selon les degrés d’affinité avec les mathématiques

Étant donné la multiplicité et la diversité des sciences, il semble impératif de procéder à un regroupement des disciplines scientifiques fondé sur leur apparentement avec les mathématiques. Le choix d’un tel critère nous semble plus judicieux que celui qui repose sur les catégories, traçant dans certains cas une frontière nette entre les sciences^[12]. Suivant le conseil de Comte, selon lequel la classification doit « être déterminée par les affinités réelles » (Comte, 1852 [1830] : 52) entre les disciplines, nous optons pour le degré d’affinité comme critère de classement. Ainsi, on considèrera que le degré d’affinité entre les mathématiques et la physique est plus fort que le degré d’affinité entre les mathématiques et l’éducation à la citoyenneté, d’autant plus que les deux premières disciplines ont en commun la majorité de leurs outils conceptuels, leurs métalangues ainsi que leurs démarches. Nous précisons que le degré d’affinité^[13] n’exclut pas l’interaction entre les disciplines. Que ce degré soit fort ou faible, le plus important, ce sont les liens possibles qu’on établit entre les disciplines qui comptent. Ce degré n’est qu’un indicateur du volume du travail à faire pour relier deux disciplines : plus le degré est faible, plus on devra fournir d’efforts pour trouver des liens; plus il est fort, plus facile est la recherche des liens.

Sur la base des matières scolaires enseignées au secondaire, nous avons identifié trois groupes :

• les matières de premier degré d’affinité : physique, informatique, économie, chimie, technologie;
• les matières de deuxième degré d’affinité : géographie, science de la vie et de la terre, éducation physique et sportive;
• les matières de troisième degré d’affinité : langues, arts, phonétique, histoire, éducation à la citoyenneté, la religion.

Cette sériation des disciplines scolaires n’est qu’une étape dans la mise en place de l’interdisciplinarité scolaire, un des éléments clés de la MCA. Bien évidemment, le tout n’est pas dans ce regroupement, il faut définir à la fois le cadre et les modalités d’implémentation de cette interdisciplinarité. De manière concrète, il faut élaborer des tâches ou des activités pédagogiques qui permettront de faire ressortir des liens entre les disciplines.

Si on s’inspire des résultats des travaux de Hasni et al. (2012), dans les pratiques, deux tendances s’observent. La première tente d’associer une discipline et un contexte d’apprentissage en dehors de l’école. C’est ainsi qu’on parle du rapport entre les mathématiques et la vie quotidienne : le menu dans une cafétéria, la performance (statistique) d’une équipe de basketball, l’analyse des empreintes digitales sur une scène de crime (Hasni et al., 2012). Comme on le constate, ce sont là des situations de vie au cours desquelles l’apprenant·e est appelé·e à mobiliser des savoirs relevant de plus d’une discipline : mathématiques, restauration, statistiques, criminologie, etc. La seconde tendance consiste à identifier clairement les éléments de deux ou plusieurs disciplines afin de montrer leurs liens; par exemple, le recours aux mathématiques lors d’un cours de technologie, d’informatique, de géographie, etc.

L’expérience canadienne décrite par Hasni et al. (2012) repose sur une démarche bien précise. Il s’agit de l’enseignement par projet ou pédagogie du projet, qui désigne « les démarches et les approches d’enseignement et d’apprentissage en classe recourant au projet. » (Hasni et al., 2011 : 8). Il est donc capital de voir dans quelle mesure une telle approche peut être applicable dans le contexte africain, et surtout de vérifier sa compatibilité avec l’approche par les compétences qui semble être promue dans de nombreux états africains aujourd’hui^[14] (Roegiers, 2008). En ce qui nous concerne, nous pensons que l’élaboration et la réalisation d’un projet, en tant qu’activité pédagogique, ne devraient poser aucun problème dans le système éducatif des états africains d’autant plus qu’elle va permettre de résorber l’écart entre l’apprentissage en milieu scolaire et l’apprentissage dans la vie. Le projet constitue un élément fondamental de l’approche.

Ainsi, les élèves élaborent leur projet d’apprentissage, une réalisation qu’ils se proposent de faire et qu’ils ont eux-mêmes choisie (même s’ils sont guidés par un adulte dans leur choix) et qu’ils gèrent personnellement. Les projets choisis amènent les élèves à faire des apprentissages individuels et en groupe. […] Ces apprentissages ne peuvent se réaliser que si les élèves sont engagés dans leurs projets, sont responsables de leur production, recherchent des moyens de développer les ressources nécessaires à mener à terme leurs projets et surtout, peuvent expliciter et justifier leurs apprentissages et analyser les obstacles rencontrés et les défis relever [sic]. (Lafortune, 2010 : 17)

Toute la pertinence de l’approche, nous semble-t-il, se trouve dans la conception double des apprentissages, des savoirs comme un fait institutionnalisé et en même temps, comme un fait social. Le va-et-vient entre l’école et la vie se double du va-et-vient entre les disciplines. Par ailleurs, l’idée même d’élaborer un projet a pour conséquence positive de positionner l’apprenant·e dans la posture d’un acteur ou d’une actrice engagé·e, et celle de la responsabilisation sociale. Ce sont là deux qualités et deux exigences auxquelles l’apprenant·e devra faire face dans la vie. Au demeurant, la pédagogie du projet favorise la pratique de l’interdisciplinarité non seulement en établissant des passerelles entre la vie et l’école, mais en explicitant et en renforçant également les liens interdisciplinaires. Nous examinerons quelques exemples d’interrelations entre les mathématiques et les autres disciplines^[15].

Quelques cas illustratifs d’interactions des mathématiques avec d’autres disciplines

Le cas des matières de premier degré d’affinité

Il s’agit des disciplines ou des domaines de connaissances dont les théories sont construites dans une démarche essentiellement expérimentale et de nature mathématique. Celles-ci utilisent, en plus de sa propre métalangue, la métalangue et les outils mathématiques. Ces domaines ont constitué, pendant leur développement en interne et/ou en externe, un ensemble dynamique d’outils mathématiques nécessaires pour mieux étudier et résoudre leurs problèmes.

En économie, les économistes-mathématicien·e·s étudient les richesses, les échanges et les choix à l’aide d’outils mathématiques. L’économiste Robbins définit l’économie comme suit : « L’économie est la science qui étudie les comportements humains comme une relation entre les fins et les moyens rares à usages alternatifs. »^[16] (1932 : 15). Il s’agit donc d’une discipline qui a pour objet le comportement humain en rapport avec la gestion des ressources rares, la répartition des moyens limités à usages alternatifs entre des fins concurrentes. Contrairement à ce qui s’observe dans les sciences dites de la nature, les variables dans l’analyse économique sont rarement indépendantes et le nombre de facteurs incontrôlés reste grand. C’est ainsi qu’il est difficile de donner une interprétation ou une conclusion unique à un phénomène économique, parce qu’ici tout est dynamique selon des rapports qu’il faut induire. Les économistes en sont venu·e·s à modéliser et simuler les phénomènes économiques en définissant des hypothèses de corrélation tenues pour vraisemblables, et en simplifiant le comportement des variables et des paramètres dans le modèle. Archinard et Guerrien relèvent cette difficulté en ces termes.

La plupart du temps, lorsque l’économiste formalise mathématiquement un problème, il fait intervenir des fonctions à plusieurs variables correspondant aux biens, et à leur prix, considérés (ou encore à des agrégats tels que le capital, le travail, etc.). Très souvent cette formalisation a pour but la recherche de l’extremum d’une fonction-objectif sous contraintes. (Archinard et Guerrien, 1992 : 219)

Malgré les divergences constatées entre les écoles, les mathématiques ont une place importante dans les théories économiques. L’économiste se sert constamment de la dérivée d’une fonction économique (utilité marginale, productivité marginale, taux de substitution de biens, coût) lorsqu’il/elle cherche à déterminer les extremums d’une fonction (utilité, demande, profit, offre).

 Pour ce faire, des notions et outils mathématiques comme les dérivées en chaîne ou partielles, les fonctions implicites, le développement de Taylor généralisé, les fonctions concaves ou convexes, la programmation linéaire (méthode simplexe des transports), la programmation dynamique, l’ordonnancement sont très prisés aujourd’hui. Les applications des modèles mathématiques en économie sont nombreuses et non exhaustives. Les dirigeant·e·s à travers le monde n’arrêtent de consulter les experts et les expertes mathématiques appliquées à l’économie pour étudier et proposer des actions pour leur politique économique et sociale (Lecaillon, 1974).

À l’échelle microéconomique, les jeunes en quête d’emploi doivent savoir que le mathématicien et la mathématicienne est un peu comme un philosophe des sciences exactes.

L’entreprise ne recrute pratiquement jamais de mathématiciens en tant que tels, mais doit satisfaire des besoins mathématiques par l’emploi de personnels de formation mathématique, capables de maintenir une veille technologique, de traduire et d’appliquer des travaux théoriques. (Guillopé, Helffer, Pansu & Prural, 1998/1999 : 21)

Toute entreprise soucieuse de faire augmenter son profit, aussi bien dans la production que dans les ventes, recrute son personnel parmi les mieux outillés en mathématiques parce que des mathématiques utilisées de manière adéquate favorisent mieux la structuration de nouvelles connaissances, apprennent à penser dès les premières séances de formation, développent des aptitudes et des attitudes. Depuis bientôt plus d’une vingtaine qu’on rencontre de plus en plus des mathématicien·ne·s dans le domaine de la finance et de la banque. De même, ces entreprises travaillent en étroite collaboration avec les universités qui leur fournissent une quantité non négligeable de leur personnel. L’un des exemples les plus parlants est celui de l’universitaire français, Grégoire Loeper, maitre de conférences à l’université de Lyon. Il décide de se tourner vers une grande banque de la place qui finit par le recruter. Il concilie ainsi ses qualités de chercheur en mathématiques fondamentales aux expériences en entreprise en mathématiques financières : « les mathématiques financières forment un domaine très technique, c’est pour cela que nous valorisons le doctorat au sein de l’équipe de recherche. C’est la preuve que vous êtes capable de poursuivre une démarche scientifique de manière autonome. » (Loeper, cité par FSMP [s.d.]). Une autre option pour l’entreprise qui veut prospérer est qu’elle s’associe toujours à un cabinet de conseil pour un suivi scientifique et technique du déroulement de ses activités, évitant ainsi des situations pouvant conduire à la faillite.

En physique, l’on utilise des modèles mathématiques pour étudier la dynamique des phénomènes physiques. La physique est en général le domaine le plus ancien bénéficiant le plus d’applications de modèles mathématiques. D’ailleurs, l’élément fondamental de la matière qu’est l’atome est mieux décrit par une construction mathématique que par une image physique. Dans le tableau périodique des éléments de Mendeleïev, l’atome est décrit mathématiquement par quatre équations ou nombres quantiques. Cette description est d’ailleurs complétée par la structure électronique de l’atome qui décrit rigoureusement la capacité de ce dernier à réagir ou à se mouvoir dans un milieu. La physique qui tente d’expliquer les phénomènes naturels de l’univers passe par une construction qui se veut objective. Cette construction constitue le résultat d’une théorie mathématique préalable et axiomatisée (Roy, 1979).

Le 15 mars 2015, un mini-séminaire est organisé à l’Université de Ngaoundéré par un groupe d’étudiant·e·s sur le thème « Mathematics and Computer for All » (MathComp4ALL)^[17], où il était question des interactions entre les mathématiques, l’informatique et les autres sciences. À la question « Pourquoi étudier les mathématiques et l’informatique quand on veut être physicien? », un doctorant en sciences physiques déclare : « Nul n’est physicien s’il n’est d’abord mathématicien ». Il ajoute :

Une expérience en physique est un protocole matériel permettant de mesurer certains phénomènes dont la théorie donne une représentation conceptuelle. Il est donc illusoire d’isoler une expérience de physique de la théorie mathématique associée, sinon cette théorie serait vaine pour le physicien. Le physicien ne mesure évidemment pas les choses au hasard; il faut qu’il ait à l’esprit l’univers conceptuel d’une théorie […]. La physique mathématique n’est autre qu’un domaine de recherche commun à la physique et aux mathématiques s’intéressant au développement des méthodes mathématiques spécifiques aux problèmes physiques ou plus généralement à l’application des mathématiques à la physique; et à l’opposé, aux développements des mathématiques que suscitent certains domaines de recherche en physique^[18].

En effet, les sciences physiques se prêtent mieux aux liens interdisciplinaires avec les mathématiques dans des contextes convoquant des notions mathématiques comme l’étude des systèmes d’équations aux dérivées partielles, des algèbres aux symétries particulières, des méthodes de décomposition en séries, de la géométrie riemannienne ou pseudoriemannienne, de la théorie des groupes très utilisée en physique théorique, notamment pour le développement des théories de jauge, etc. Au-delà de ces liens, la physique, dans sa démarche de représentation expérimentale des théories mathématiques, s’est confrontée à un certain nombre de problèmes comme le coût élevé des séries d’essais réels, la résolution analytique des équations mathématiques y afférentes, le temps de calcul très long dans certains cas. Ces difficultés et l’essor des techniques au XXe siècle font naître une nouvelle science : la simulation informatique ou numérique. Il s’agit d’une expérience sur le modèle théorique à l’effet de dégager une représentation du phénomène réel.

Sans rentrer dans les détails techniques de leur manipulation, relevons quelques exemples de modèles mathématiques utilisés en physique :

• méthodes de Runge-Kutta pour le traitement numérique des équations différentielles;
• simulation atomistique en physique des matériaux;
• méthode de Monte-Carlo en physique statistique, physique des matériaux, physique nucléaire, physique des particules, mathématiques, statistiques et économétrie;
• méthode ab initio en mécanique quantique;
• discrétisation des équations en mécanique, aérodynamique, acoustique;
• simulations PIC (Particle In Cell) en physique;
• méthode DPSM en ultrasons, électrostatique, électromagnétisme;
• méthodes de simulation en géostatistique;
• expérience de Fermi-Pasta-Ulam en physique.

En fait, les physicien·ne·s, doublé·e·s de compétences en mathématiques, dessinent la configuration a priori de l’espace ou de l’univers où vont s’inscrire les phénomènes physiques. Il s’ensuit la construction de modèles mathématiques pour les décrire. Par exemple, la théorie des groupes avec le groupe de Lorentz est fondamentale pour la relativité restreinte. Cette théorie joue également un rôle capital dans la physique des particules. Elle a conduit à découvrir de nouvelles particules élémentaires comme les atomes. Un autre exemple est la notion mathématique de linéarité mise en application en sciences physiques. Ici, on désigne par phénomènes physiques linéaires, les phénomènes où une grandeur est une fonction linéaire de certains paramètres. Autrement dit, ce sont les phénomènes dans lesquels la fonction f qui, à une cause associe son effet, obéit aux propriétés de linéarité.

Ceci se traduit par :

• f préserve l’addition (+) :

si on ajoute deux causes, l’effet produit est la somme des effets; on traduit cet algorithme par si f(cause1) = effet1 et f(cause2) = effet2, alors f(cause1+cause2) = effet1+effet2; dans ce cas, on dit que les effets se conjuguent.

• f préserve la multiplication externe (ou multiplication par des scalaires) (*) :

si on augmente (ou duplique) une cause, l’effet conséquent est augmenté dans le même ordre de grandeur; on traduit par f(λ*cause1) = λ*effet1; ici, on dit que les effets se superposent.

Les propriétés mathématiques des applications linéaires donnent alors des outils efficaces pour étudier ce type de phénomènes. Les formidables progrès enregistrés actuellement dans l’industrie automobile, l’aviation, le chemin de fer, l’électronique, pour ne citer que ces domaines-là, sont des preuves assez éloquentes du dynamisme de ces interactions.

En chimie, les chercheurs et chercheuses formé·e·s en mathématiques utilisent les outils mathématiques pour étudier la dynamique des concentrations. La théorie des groupes contribue à décrire les symétries que présentent les molécules et les cristaux. Dans une pratique élémentaire, le calcul du pH^[19] d’une solution aqueuse par exemple permet d’évaluer son acidité ou sa basicité. Il se fait après la détermination de sa concentration en ions hydronium H3O+ (en moles/litres) selon la formule : pH = -log[H3O+]. La valeur du pH est comprise entre 0 et 7 pour une solution acide; elle est égale à 7 pour une solution neutre et elle est comprise entre 7 et 14 pour une solution basique. La thermodynamique chimique, la loi des gaz parfaits, la radioactivité, l’interprétation mathématique des réactions chimiques sont des domaines qui font appel à d’importants outils mathématiques. On peut citer entre autres :

• méthode ab initio en chimie quantique;
• système multi-agents pour la simulation de systèmes complexes;
• dynamique moléculaire, dynamique d’amas en chimie physique.

En cryptologie^[20], les outils mathématiques sont utilisés pour assurer la sécurité et la confidentialité de l’information. Le but de la cryptographie est d’assurer, en la sécurisant, la confidentialité de l’information entre deux personnes qui communiquent, de sorte qu’une tierce personne qui l’intercepte ne puisse pas la comprendre ou la modifier. Deux types de procédures ont été développés pour cet usage : algorithmes à clés secrètes et algorithmes à clés publiques.

Dans le premier type, on peut citer le chiffrement à flot, par blocs (itératifs) et par décalage; qui est un vieil exemple que les Allemands ont utilisé pendant la Seconde Guerre mondiale (Singh & Coqueret, 2002; Brisson & Téberge, 2013). Le problème le plus important ici réside dans l’échange de clés entre celui ou celle qui émet le message et celui ou celle qui le reçoit. Si la clé est interceptée, le message perdra automatiquement de sa confidentialité.

Dans le second type d’algorithme, ce problème est levé. Le système de chiffrement RSA^[21] inventé en 1978 et le cryptosystème d’El Gamal en sont deux exemples; le premier système est aujourd’hui très utilisé par les services secrets modernes. Dans ce type, l’algorithme de chiffrement et la clé sont connus ou libres d’accès pour tous, mais il n’est pas possible d’en déduire directement le procédé de déchiffrement. De nos jours, ce système s’applique dans la télécommunication par internet où nous avons une adresse de courrier électronique, qui est une clé publique qu’on peut donner à tout le monde, couplée d’un mot de passe qui est une clé privée que seul·e l’usager ou l’usagère détient, à moins que l’on décide de la communiquer à quelqu’un d’autre.

En général, les opérations de codage de l’information sont appelées « algorithmes de cryptage » ou « de chiffrement ». On distingue plusieurs types : le chiffrement par décalage, le chiffrement affine, le chiffrement logarithmique… Les opérations de décodage sont des « algorithmes de décryptage » ou « de déchiffrement ». Par ailleurs, la théorie des codes correcteurs permet de sécuriser la communication en détectant et en corrigeant les inévitables erreurs qui affectent les échanges d’information numérisée. Ici, les spécialistes du codage font usage des méthodes algébriques ou géométriques abstraites pour la plupart. Généralement, les notions d’algèbre telles que les groupes, les graphes, les corps finis, la théorie des nombres premiers, le codage et l’algorithmique, les courbes elliptiques, les fonctions logarithme et exponentielle de base réelle sont très sollicitées. Dans une situation de classe, on peut demander à l’apprenant·e d’utiliser le processus de chiffrement par décalage de clé 3 pour coder le mot MATHEMATIQUE et pour déchiffrer le mot CLQPL.

Le cas des matières de deuxième degré d’affinité

Il s’agit des domaines de connaissances dont les théories sont construites dans une démarche procédurale ou expérimentale et utilisant une métalangue mixte (celle de la discipline en question et celle des mathématiques). Ces domaines ont constitué, pendant leur développement, un ensemble dynamique d’outils mathématiques nécessaires pour mieux étudier et résoudre leurs problèmes. On peut citer entre autres l’épidémiologie mathématique, la démographie, la criminologie et le sport, notamment le football.

En épidémiologie, les outils mathématiques aident à modéliser, analyser, simuler et prédire les phénomènes. Cette modélisation et cette simulation sont sous-tendues par les mathématiques. Ces opérations sur les maladies infectieuses ont longtemps intéressé les biomathématicien·ne·s au point de devenir des éléments d’aide à la prise de décisions relativement aux risques sanitaires majeurs. Elles jouent également un rôle important dans la prévision de l’évolution des maladies, tout comme dans la comparaison des effets de différentes stratégies de lutte contre ces maladies. Il existe de nombreux exemples d’études de ce genre sur le VIH (Alassane, 2012; Bichara, 2013), les hépatites virales (Kouakep Tchaptchié, 2017), le paludisme (Tewa, 2007) et les infections multirésistantes. Il y a également des modèles intra-hôtes qui sont utilisés en cancérologie (Goldwirt, Lebbé & Mourah, 2015).

Il faut toutefois noter qu’à la différence d’autres sciences, l’épidémiologie mathématique ne se prête pas à la validation expérimentale des modèles étudiés, car dans la plupart des cas les expérimentations sont difficiles à réaliser pour des raisons éthiques. De manière générale, l’une des techniques de modélisation la plus prisée en biologie est l’analyse compartimentale. Il s’agit d’introduire des équations différentielles ordinaires ou des équations aux dérivées partielles pour écrire et analyser le modèle décrivant la dynamique de l’évolution par phases ou compartiments d’une maladie au sein d’une population. C’est ainsi qu’une maladie évoluant sur quatre phases – infection, incubation, contamination et guérison totale – sera décrite par un modèle compartimental dénommé SEIR. Cet acronyme est constitué des initiales des noms désignant les catégories d’individus se trouvant dans la même phase de développement de la maladie, appelées « compartiments » : S pour le compartiment des individus sains et susceptibles de contracter la maladie, E pour le compartiment des individus exposés à la maladie, I pour le compartiment des individus infectieux et R pour le compartiment les individus rétablis après ou sans traitement.

Les modèles intra-hôtes sont des modèles qui décrivent l’évolution d’un parasite (virus, protozoaires …) responsable d’une maladie. Le calcul du taux de reproduction de base (R₀) et la position de sa valeur numérique par rapport à l’unité sont essentiels pour faire une prédiction spatio-temporelle de la dynamique de la maladie. À cet effet, il existe de nombreuses plateformes de simulations numériques de phénomènes épidémiologiques telles que Matlab, Mathematica, Maple, Sage. Ici, interviennent une pléthore de notions : systèmes dynamiques, équations différentielles ordinaires, équations aux dérivées partielles, transformation de Fourier, contrôlabilité, observabilité, stabilisation et stabilité des solutions des systèmes, distributions, les espaces vectoriels euclidiens, etc.

Prenons le cas suivant pour illustrer une interaction entre la biologie et les mathématiques. L’on veut étudier la durée de l’effet d’un médicament (sérum) dans le corps humain. On injecte dans le sang d’un individu malade, toutes les 8 heures, une quantité q₀ de ce sérum, exprimée en millilitres (ml). Après élimination naturelle par l’organisme humain, la quantité restante de ce produit dans le corps est donnée au bout d’un temps t, exprimé en heure, par la fonction suivante :

t ↦ q0e^(-t/24).

Le problème qui est posé ici relève de la biologie. La solution apportée s’appuie sur des éléments d’ordre mathématique. Dans le cadre d’une classe, on peut demander aux enfants de calculer le temps mis pour consommer plus de la moitié des 10 ml de sérum reçus. Dans ce cas,  on a : q0  = 10 ml. Il s’agit de déterminer la valeur de t pour que la quantité restante soit plus petite que 5 ml. Le modèle correspondant à cette situation est exprimé par l’inéquation,

10e^(-t/24)  ≤  5.

Soit e^(-t/24)  ≤ 1/2. En appliquant le logarithme népérien (ln) de part et d’autre de l’égalité, et en respectant la règle des signes, on obtient t ≥ 24ln2 = 16,6355 h. Soit plus de 16h 38mn 08s. Ici, interviennent les propriétés des fonctions logarithmes népériens, celles des fonctions exponentielles, ainsi que la règle des signes sur les inégalités.

D’autres interactions sont également observables dans des études relevant de domaines divers. On peut citer entre autres :

• l’évolution d’une population humaine dans le temps et suivant l’âge en recourant à des équations aux dérivées partielles;
• la datation au carbone 14 et les explorations minières par l’utilisation de la topologie algébrique;
• les croisements en génétique au moyen de la théorie des nœuds.

En démographie, le modèle logistique de croissance ou de décroissance reste d’actualité. Pour étudier les variations de la population humaine, un premier modèle mathématique a été établi. Si y(t) désigne la quantité (croissante ou décroissante) de la population enregistrée à une date t, alors la quantité y = y(t) a un taux exponentiel de croissance ou de décroissance si pour une constante k, on a

(1) : dy/dt = ky.

Si k > o, on dit que y croit de façon exponentielle; et lorsque k < o, on dit que y décroît de la même façon. L’équation (1) représente la loi de croissance ou de décroissance exponentielle (Hurley, 1980 : 504).

Mais on remarque que si k > 0, alors y tend vers l’infini lorsque t tend vers l’infini. Autrement dit, si le coefficient de croissance est supérieur à 0, alors la population augmente indéfiniment dans le temps. Or, les ressources nutritives de la terre étant limitées, on constate que dans ce cas, il est impossible de subvenir aux besoins alimentaires d’une population humaine infiniment grande. Afin de résoudre l’équation, on a été amené à réduire volontairement k à zéro (croissance humaine nulle). Une telle situation catastrophique ne pouvant provenir que des calamités comme la famine, les épidémies ou une guerre nucléaire, pour réduire k à la valeur zéro ou en dessous de zéro. On aboutit donc à une impasse du fait d’une discordance entre le modèle mathématique et la réalité sociale et humaine. Le modèle (1) étant inapplicable, il fallait en élaborer un nouveau.

Aussi, les démographes outillé·e·s en mathématiques se sont mis·e·s à la recherche d’un modèle plus cohérent. Après des observations sur des colonies d’insectes, de bactéries et même des rats, ils/elles ont constaté que pour des valeurs très grandes de la population (y), le taux de mortalité croissait rapidement et la reproduction décroissait aussi rapidement suite à la détérioration des ressources nutritives et des conditions de vie (Hurley, 1980 : 504-505). Ceci a conduit à la construction de ce qu’on a appelé modèle logistique de croissance traduit par l’équation

(2) : dy/dt = ky-ly² ,

où k et l sont des constantes strictement positives et y représente la fraction de la population à une date t. La solution mathématique de cette équation d’inconnue y est donnée par la formule y = (kKexp(kt))/(1+lKexp(kt)), avec K = +exp(kc); le réel c étant une valeur constante.

Ce deuxième modèle a comblé presque toutes les attentes. En clair, l’on comprend l’importance de la régulation des naissances puisque le facteur l, qui conditionne l’équilibre entre la croissance de la population et les ressources, relève soit d’une volonté humaine de réduire les naissances, soit le résultat d’une calamité. Aujourd’hui, les recherches sont suffisamment avancées sur cette thématique. Dans ce contexte, nous notons l’utilisation des notions de calculs différentiels, de croissance comparée de fonctions. Ce genre de sujets peut être exploré dans les lycées afin d’établir des liens entre les mathématiques (calculs différentiels), la géographie (étude de la démographie) et la SVT (étude de la reproduction humaine, la régulation des naissances).

En criminologie, la loi du refroidissement de Newton aide la police scientifique à peaufiner certaines enquêtes. Les polices criminelles dotées de moyens technologiques sophistiqués se fondent désormais sur des outils mathématiques pour affiner leurs enquêtes : la collecte et l’analyse des preuves, l’analyse psychosociale de la personnalité d’une personne suspecte et l’établissement du profil de l’individu suspecté. Elles sont d’ailleurs couramment appelées « polices scientifiques ». La situation suivante illustre le rôle que peuvent jouer les mathématiques dans la résolution des enquêtes criminelles.

Dans un bâtiment, il fait 21°C. À 14 heures, une victime d’un meurtre est retrouvée par un agent qui appelle immédiatement la police. Cette dernière arrive à 15 heures et trouve que le corps de la victime présente 31°C. Mais une heure après, cette température retombe à 29°C. En supposant que la victime présentait une température de 37°C avant la mort, quelle serait l’heure probable du crime? La détermination de l’heure du crime pourrait, en fonction des emplois du temps des différentes personnes suspectées, permettre de resserrer davantage l’étau autour du meurtrier.

Il convient de préciser que le refroidissement du corps de la victime peut s’expliquer par un phénomène mathématique de décroissance exponentielle d’un corps placé dans un milieu ambiant. Ce phénomène est modélisé par la loi du refroidissement de Newton (Hurley, 1980 : 507) qui s’établit comme suit :

Si T(t) est la température en degré centigrade d’un corps à l’instant t, si C est la température (supposée constante) en degré centigrade du milieu environnant, alors le taux k de refroidissement du corps est défini par l’équation différentielle,

(E) : dT/dt = k(T-C).

Ce qui conduit à la relation ln|T-C| = kt+c1; c1 étant une valeur constante qui se définit à la date t = 0 par l’égalité c1 = ln/T₀-C/ où T₀ est la valeur de T à t = 0. On obtient alors le coefficient k = (ln|T-C|-c1)/t, qui permet de retrouver l’heure demandée, t₀ = (ln16-c1)/k.

En d’autres termes, pour déterminer l’heure, on a besoin de mettre en relation la température du corps de la personne décédée, la température du milieu ambiant, l’heure à laquelle on l’a retrouvée, combinées selon des principes de multiplication en puissance logarithmique. Mais dans le cas où la victime présente déjà une température corporelle nulle au moment de sa découverte, les calculs deviennent plus difficiles.

Pour la résolution du problème, on peut procéder comme suit :

• identification des variables : C = 21;

À la date t = 0, T₀ = 31;

À la date t = 1, T₁ = 29;

• résolution : on a c₁ = ln10 et k = ln(0,8).

Sachant qu’au moment du crime, la victime avait 37 °C de température, on a t₀ = (ln16-c1)/k, soit t₀  = -2,10628. L’heure du crime t_c est donc donnée par t_c = 14 + t₀. Soit t_c ≈ 12h 30. On conclut alors que la victime aurait été tuée autour de 12h 30. Les notions qui interviennent ici sont les équations différentielles et les fonctions logarithmes népériennes. Bien évidemment, cet exemple ne saurait être appliqué au lycée. Ce qui est visé ici, ce sont tout simplement les potentialités offertes par les outils mathématiques pour résoudre des problèmes concrets qui se posent à la société. L’illustration reste cependant utilisable dans le cadre des institutions spécialisées telles que les écoles de police.

En sport, notamment en football, les outils mathématiques comme les statistiques, les probabilités, l’analyse des données, la géométrie permettent aux entraîneurs et entraîneuses avisé·e·s de prévoir et d’anticiper leurs victoires, en prenant des décisions sur la gestion matérielle et humaine de leur équipe.

De même, les statistiques mathématiques proposent des perspectives qui expliquent les occurrences de jeu, fournissent des classements comparatifs des équipes et des joueurs, et aident à la prise de décision par les entraîneurs et la direction de l’équipe. Les sources habituelles de statistiques sont les données concernant les passes, les courses, la défense, les coups de pied, les revirements et la gestion du temps^[22]. (Greenwald & Thomley, 2012 : 399)

Le cas des matières de troisième degré d’affinité

Certains domaines de connaissances construisent leurs théories avec leurs propres outils, mais qui parfois s’appuient sur un ou plusieurs éléments appartenant aux mathématiques :

• des principes de la démarche mathématique pour bâtir leur raisonnement;
• la modélisation et simulation mathématiques pour étudier la dynamique spatio-temporelle de certains phénomènes physiques;
• des études statistiques (et donc mathématiques) pour valider ou infirmer des hypothèses.

Nous pouvons citer, entre autres, les disciplines telles que la sociologie, la psychologie, la linguistique.

En sociologie comme en psychologie, certains tests et sondages sont conduits avec des outils statistiques. Ces disciplines utilisent des outils mathématiques comme la théorie de l’échantillonnage, les tests d’hypothèses, de convergence ou de lois sur les données mesurables pour vérifier leurs hypothèses de recherche. Elles se situent dans le champ des sciences sociales ou humaines qui, comme l’économie, la science politique, étudient les comportements collectifs des humains dans un milieu. Pour ce qui est de la sociologie singulièrement, on peut établir des points de contact entre elle et d’autres sciences. Elle peut partager avec ces sciences les mêmes sujets ou problématiques d’étude, et même développer des liens interdisciplinaires. La sociologie de la connaissance aborde l’étude des idéologies ainsi que des représentations collectives (Durkheim, 1912). Il n’y a pas longtemps, la sociologie des sciences et des techniques s’est dotée d’instruments pour analyser la production de connaissances et des outils scientifiques (Merton & Norman, 1973; Latour, 1989).

Le psychologue Estes (1960) a proposé un modèle mathématique pour « mesurer » l’intelligence d’un individu. Ce modèle définit une fonction k(t) comprise entre 0 et 1 comme étant la probabilité à un instant t, qu’une personne aurait à répondre correctement à une question donnée. Pour Estes, apprentissage signifie « changement » (volontaire et positif) de k(t). Pour essayer de traduire le phénomène observé, c’est-à-dire que les individus apprennent à des degrés différents, il modélise le changement de k(t) de la manière suivante : si un acte utile (comme étudier, aller en classe ou traiter un exercice) est réalisé, alors k(t) devient k(t) + c(1- k(t)), où le c compris entre 0 et 1, est un coefficient individuel d’étude qui peut être mesuré par un instrument comme le quotient intellectuel^[23].

Si un acte négatif est passé (comme « manquer » un cours ou « ne pas » traiter son exercice), alors k(t) devient k(t) – ck(t). Si λ (0 ≤ λ ≤ 1) mesure le pourcentage du temps favorable dont l’apprenant·e dispose pour poser des actes utiles, alors une formule pour mesurer son intelligence à l’instant t est k(t) = λ + ce^-ct, qui est une solution de l’équation différentielle : dk/dt = λc-ck(t) = λc[1-k(t) – c(1-λ)k(t)]. Ici, le réel « c » est une constante égale à la mesure (raisonnable) de l’aptitude d’une personne à apprendre. En effet, si c = 0, alors la personne ne peut pas apprendre du tout. Quoi qu’elle fasse, son intelligence ne changera jamais. Mais si c se trouve très proche de l’unité, c’est-à-dire de 1, l’activité positive ou utile fait croître rapidement k(t) vers la valeur 1, de sorte que l’individu est taxé d’excellent ou super apprenant. Ainsi, ce modèle montre que l’intelligence humaine n’est pas seulement héréditaire, mais elle est aussi tributaire de multiples efforts déployés dans toute activité cognitive. Ici, nous notons l’utilisation des statistiques et des équations différentielles ordinaires avec contraintes.

En linguistique, la recherche sur la construction du sens est tellement avancée qu’aujourd’hui des modèles à fondement logique liés aux valeurs de vérité se distinguent singulièrement par leur rigueur, leur cohérence interne et leur capacité explicative. Le traitement à l’ordinateur de l’information en tire grandement profit. Dans ce contexte, un personnage n’est plus perçu par sa psychologie, mais comme une fonction. Martin définit l’univers de croyance d’un locuteur donné comme « l’ensemble des propositions que, au moment où il parle, le locuteur tient pour vraies. » (1983 : 7). Il établit donc un rapprochement entre les propositions linguistiques et les propositions logiques. Cet univers sera réinterprété, en termes mathématiques, comme l’ensemble des propositions décidables, c’est-à-dire celles dont le locuteur est à même d’attribuer une valeur de vérité : vrai, faux, possiblement vrai, possiblement faux. Si l’on admet que la valeur +V (plus ou moins vrai) représente l’infinité des valeurs comprises entre 0 et 1, alors cette application sera une surjection. La notion d’univers de croyance est alors susceptible d’être quantifiée et modélisée de sorte qu’on puisse passer aisément de la vérité subjective à la vérité analytique (Martin, 1987).

Par ailleurs, au cours de l’une des nombreuses conférences scolaires^[24] sur le thème « Science et littérature : quelle complémentarité? », Mani Kono, enseignant de français, déclarait dans son exposé : « la littérature est utile à l’homme pour transmettre le message et la mathématique utile à l’homme pour ses règles et surtout sa démarche. »^[25] Pour clarifier son argumentation, il s’est appuyé sur le schéma ci-dessous et a conclu en disant « la littérature utilise les mathématiques pour mieux faire accéder à la dimension message qui est cachée. »

Cette formule tente un rapprochement entre les mathématiques et la narratologie. Elle se lit comme suit : l’algorithme, qui est ici le récit, est une fonction qui contient un message dont la compréhension dépend des paramètres précis que sont les actants^[26]. Cependant, cette symbolisation ne devrait en aucun cas être considérée comme l’application d’un théorème mathématique, donc extérieur aux études littéraires. Il s’agit davantage d’une adaptation des concepts mathématiques pour expliquer, décrire et analyser des textes littéraires, ou pour élaborer une théorie générale de la narration. Dès la fin des années 1960, de nombreuses tentatives d’exploration des liens possibles entre mathématiques et études littéraires ont foisonné. On peut citer notamment les travaux de Christeva dans le domaine de la sémanalyse (1969). Précisons toutefois que des critiques sur ces travaux ont été faites par Sokal & Bricmont (1997). Mais ce n’est pas ici l’objet de notre travail.

Le recours aux symboles mathématiques procède plus d’une quête de la rigueur par le biais de la formalisation que de la recherche d’une quelconque vérité qui serait unique. Aussi, les chercheurs et chercheuses en sciences humaines qui empruntent aux mathématiques leurs outils ne se prennent pas pour des mathématiciens et mathématiciennes attitré·e·s. C’est d’ailleurs ce qu’affirme le linguiste Chomsky.

Dans mon propre travail professionnel, j’ai abordé une variété de domaines. J’ai fait du travail en linguistique mathématique, par exemple, sans diplôme professionnel en mathématiques. Dans ce domaine, je suis complètement autodidacte et pas très bien formé. Cependant, j’ai souvent été invité par les universités à parler de linguistique mathématique lors de séminaires et colloques sur les mathématiques. Personne ne m’a jamais demandé si j’étais qualifié pour parler de ces sujets; les mathématiciens ne s’en offusquent pas. Ce qu’ils veulent savoir, c’est ce que j’ai à dire. Personne ne s’est jamais opposé à mon droit de parole, me demandant si j’ai un doctorat en mathématiques ou si j’ai suivi des cours approfondis dans cette matière. Cela ne leur serait jamais venu à l’esprit. Ils veulent savoir si j’ai raison ou tort, si le sujet est intéressant ou non, si de meilleures approches sont possibles. La discussion a porté sur le sujet, pas sur mon droit d’en discuter^[27]. (Chomsky, 1979 : 6)

Ces propos dévoilent une fois de plus le caractère transversal des mathématiques et surtout la rigueur et l’humilité des mathématiciens et des mathématiciennes qui s’intéressent plus à l’importance de la problématique du sujet et de la méthodologie adoptée qu’à la légalité ou la légitimité de l’orateur. C’est une manière d’envisager les relations entre les disciplines scientifiques en termes de complémentarité et de collaborations avec des résultats beaucoup plus féconds que dans une situation et un environnement cloisonné. Les possibilités restent nombreuses autant que l’imagination et la créativité de l’esprit humain peuvent en concevoir. Les disciplines souvent considérées comme étant situées aux antipodes les unes des autres peuvent retrouver des points communs, des dénominateurs communs, les points d’intersection. C’est ainsi qu’on peut lire l’analogie suivante dans le Dictionnaire des mathématiques.

Mais la mathématique est aussi et d’abord un langage et, de ce point de vue, intéresse les linguistes et les lexicographes. Chaque mot ou locution reçoit une définition précise et à côté de termes spécifiquement mathématiques (morphisme, simplexe…), d’adjectifs honorant un mathématicien (euclidien, eulérien, népérien…) ou une mathématicienne (noethérien…), figurent un assez grand nombre de substantifs (anneau, clan, corps, distribution, fibre, groupe, lacet, spectre, tribu…) ou d’adjectifs (complet, conforme, séparé, simple…) empruntés à la langue courante, mais avec un sens mathématique précis, où l’aspect métaphorique est d’ailleurs parfois présent (filtre, noyau, treillis…). De sorte que, au-delà de son aspect faussement ésotérique, il y a parfois une certaine poésie, voire une poésie certaine – osons aller jusque-là! -, dans le langage mathématique. Avec une pointe d’humour, un grand bol d’enthousiasme et une réserve inépuisable de persévérance, chevauchons donc (sur un paraboloïde hyperbolique, évidemment) à travers les univers mathématiques pour y découvrir les corps algébriquement clos, les endomorphismes diagonalisables, les espaces bornologiques, les fonctions holomorphes ou les produits de convolution. (Dictionnaire des mathématiques, 1997 : 6)

De ces observations, on retient que la langue mathématique, au-delà de l’aspect hermétique et détaché, est susceptible d’une certaine forme d’esthétique. L’esthétisation mathématique^[28] peut même donner lieu à une poétique (Marcus, 1968) faite d’une langue à la fois figurative et subjective : le calcul des limites qui mime les frontières de l’espace, le domaine de définition qui circonscrit un espace, etc. Ne sont-ce pas là des produits d’une métaphorisation? À l’évidence, les sujets qui relient les mathématiques et les études littéraires sont nombreux. Si l’on songe seulement à concevoir des activités et à aménager des cadres dans nos pratiques de classes, on créerait des occasions par lesquelles nos apprenants et apprenantes découvriront le plaisir des jeux de mots avec le vocabulaire mathématique, la créativité derrière la métalangue mathématique, la poéticité des figures géométriques mises en parallèle avec les calligrammes.

Dans le domaine de l’art, Delmer fait d’abord remarquer que « les mathématiques n’inspirent pas que les scientifiques. De nombreux et nombreuses artistes y ont puisé la matière de certaines de leurs œuvres. La réciproque est aussi parfois vraie, comme dans le cas de la perspective, où l’art a montré le chemin à des théories géométriques. » (2002 : 41). Un des grands adeptes de la peinture abstraite, Albert Aymé, dans son travail, utilise une démarche analogue à la recherche scientifique : « Je m’efforce d’avancer dans mon travail avec la rigueur d’un scientifique, mais sans me dissocier pour autant de la passion du poète ou du musicien. » (Aymé, cité par Delmer, 2002 : 44). La rigueur semble être la qualité la plus recherchée par les sciences humaines en mathématiques. En effet, les objets d’étude de ces disciplines se caractérisent par leur complexité^[29] et leur nature essentiellement hétérogène. Il s’agit donc de concilier hétérogénéité des objets et rigueur mathématique. Il va sans dire qu’une telle rigueur ne devrait pas être rigide, car lorsque les objets sont soumis à la déformation et à la variabilité, les règles doivent être souples. Comme on l’a vu dans plusieurs disciplines, une telle conciliation est possible, et même nécessaire, car « les activités humaines, les mathématiques et les arts sont le fait d’individus plongés dans le même climat culturel, politique, religieux. » (Delmer, 2002 : 44).

Il convient de relever qu’il existe des œuvres d’art qui semblent être de nature mathématique, apparemment cohérentes et correspondant à première vue à des objets réels. Mais en réalité, elles ne peuvent exister qu’en dessin, car elles échappent totalement à la construction mathématique. Il s’agit de sortes de constructions géométriques ou « figures impossibles », popularisées par le graveur Maurits Cornelius Escher^[30] inspiré des mathématiques. Les illusions optiques créées par ce type de figures s’expliquent par le fait que l’œil ne se concentre que sur une partie de la figure et non sur sa totalité.

La phonétique acoustique étudie « les propriétés physiques des ondes sonores de la parole (traitement du signal), leur mode de transmission dans le milieu, et le fonctionnement des générateurs acoustiques de l’appareil vocal qui donne naissance à ces ondes. » (Dubois et al., 2002 : 6). Le son, défini comme une onde vibratoire périodique ou apériodique (Bentov, 1991) fait l’objet de mesures, de segmentations et d’interprétations par les phonéticiens et phonéticiennes. Parmi ses composantes, on identifie la fréquence du fondamental de la voix (F₀) exprimé en hertz (Hz), l’intensité vocalique exprimée en décibels (dB), la durée ou la quantité, les pauses silencieuses exprimées en secondes, l’accentuation. La sensibilité de l’oreille aux variations d’intensité sonore étant très différente selon la hauteur de la voix, il est établi mathématiquement que la perception humaine du son dépend de l’intensité sonore qui varie entre 10^-16 et 10^-2 Watt par centimètre carré (Essono, 2006 : 144). En fait, le décibel exprime un rapport d’intensité par rapport à une intensité de référence que l’on choisit de manière arbitraire. L’équivalent en décibels d’un rapport d’intensités correspond à dix fois le logarithme décimal de ce rapport (Dubois et al., 2002 : 252). Soit, le niveau sonore N = 10log₁₀ (I/I₀), où I est l’intensité sonore et I₀ une intensité sonore de référence. Ce niveau sonore permet de connaitre la limite à ne pas franchir par rapport au seuil d’audibilité^[31] pour l’oreille humaine. L’analyse acoustique d’un son complexe consiste alors à déterminer le nombre, la fréquence et l’amplitude (l’intensité) des vibrations qui le constituent.

Une telle analyse peut se faire selon différentes méthodes. Premièrement, elle peut se faire par une analyse mathématique de la courbe à l’aide du théorème de Fourier, selon lequel « toute forme d’onde périodique de fréquence F, peut être décomposée en un certain nombre d’oscillations régulières et simples, ayant des fréquences une fois, deux fois, trois fois … N fois plus grandes que la fréquence de base. » (Fourier, cité par Essono, 2006 : 140).

Autrement dit, toute fonction T-périodique ƒ, continue dans le cas présent, peut s’écrire comme somme de fonctions sinusoïdales.

Ceci permet de distinguer, pour un corps vibrant donné, d’une part, la fréquence de vibration du corps en entier, appelée fondamental; et d’autre part, la fréquence de vibration de chacune des parties du corps vibrant, appelée harmoniques.

Deuxièmement, on peut procéder en utilisant un filtre acoustique. Ce dernier désigne « tout dispositif destiné non pas à amplifier le son en entier, mais à renforcer certaines fréquences de ce son complexe et en affaiblir d’autres. » (Essono, 2006 : 147).

Troisièmement, on peut recourir à la phonétique perceptive qui s’appuie sur l’oreille, appareil « qui transforme les signaux physiques […] en signaux nerveux qui sont ensuite décodés par le cerveau. » (Essono, 2006 : 123). Le résultat de l’analyse peut être présenté sous forme d’un spectre ayant en abscisse les fréquences et en ordonnée les intensités.

Ce type d’interactions – mathématiques, physiques et phonétique – font appel aux séries de fonctions, aux exponentielles, équations différentielles, séries trigonométriques, séries de Fourier, aux intégrales, etc.

À présent, nous souhaiterions proposer aux enseignants et enseignantes quelques pistes pouvant les aider à construire des activités qui mettent en lumière les interrelations entre les disciplines. Dans le tableau qui suit, nous proposons de partir toujours d’un problème contextualisé^[32] qui va nous permettre d’identifier les matières scolaires qui peuvent être mises en relation. Nous précisons également quelques outils conceptuels ou méthodologiques pouvant être exploités. Par ailleurs, des indications sont données sur l’organisation du travail des apprenant·e·s. Nous signalons enfin, pour nuancer, le type de relation impliquée entre les matières. Il va sans dire que ce tableau ne saurait être considéré comme un travail achevé ou un modèle prêt à usage que l’on va appliquer en toutes circonstances. Il revient à chaque enseignant et enseignante qui désire de l’exploiter, de l’adapter aux réalités et aux contraintes de sa classe. L’objectif principal reste l’édification d’une vision inclusive et collaborative de la construction des savoirs; vision qui guide et façonne toute mathématique qui se veut au service de l’épanouissement et du progrès d’une société.

Tableau 10 : Exemple de constructions d’activités qui mettent en lumière les interrelations entre quelques disciplines avec des outils conceptuels ou méthodologiques pouvant être exploités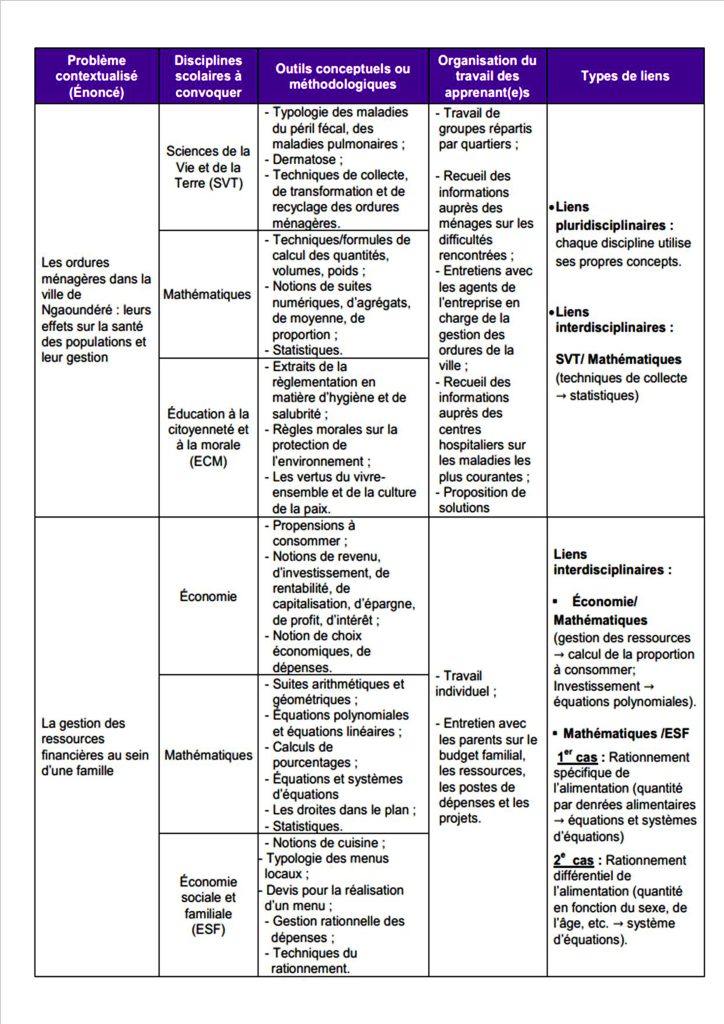

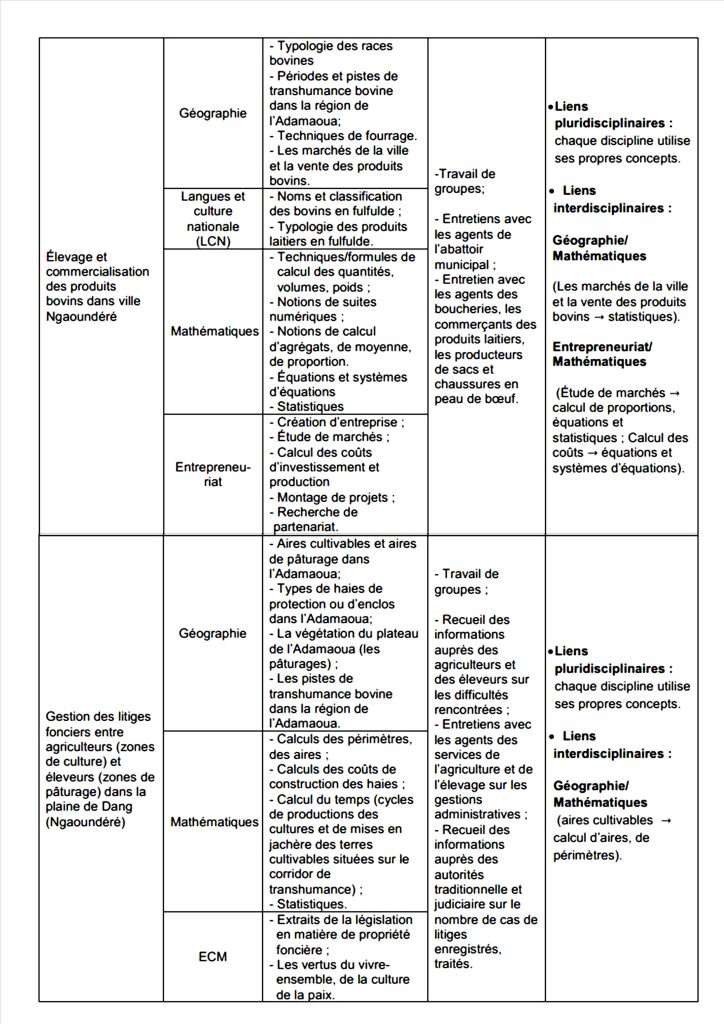
Nous tenons à préciser que les motifs, ainsi que les modalités de mise en place des activités interdisciplinaires sont à l’appréciation des guides que sont les enseignants et les enseignantes. On peut bien partir d’une simple volonté de mettre en relation des disciplines, comme on peut aussi partir d’une intuition ayant pour origine un fait de société. Si les deux démarches sont valables, la seconde semble plus fructueuse dans la mesure où elle repose sur un problème identifié, donc concret et ancré dans un contexte, celui du milieu de vie des apprenant·e·s. Dans ce qui suit, nous allons présenter un cas de figure qui nous a mis le pied à l’étrier.

Deux hommes, l’espace et la chèvre : une solution pythagoricienne à un récit mathématique

Au quartier « Hôpital » de la ville de Yokadouma (Est-Kamerun), Monsieur Tagne et son voisin Monsieur Nakoué sont en pleine discussion :

M. Tagne : Je ne voudrais plus que ta chèvre broute de l’herbe dans ma parcelle?Il faut trouver un autre endroit ou réduire la longueur, déjà assez courte, de la corde avec laquelle elle est attachée.

M. Nakoué : Les meilleures herbes se trouvent ici; mais je n’arrive pas à trouver le bon endroit pour fixer le piquet, de sorte que ma chèvre puisse brouter jusqu’aux limites de mon champ.

Pendant sa promenade, un jeune Aliakol, élève de la classe de première C au Lycée de Yokadouma, les surprend dans cette dispute.

M. Tagne : Tiens, voici notre fils Aliakol ! Il va peut-être nous aider.

Aliakol : Pourquoi les papas sont-ils en colère?

Monsieur Tagne lui expose clairement l’objet du problème. Puis le jeune élève leur demande de se calmer et d’attendre un instant, le temps pour lui de réfléchir afin de trouver une solution au conflit entre les deux voisins.

Aliakol mathématise le problème de la manière suivante : « On considère un secteur angulaire (xÂy) dont la pointe A est la borne, [Ax) et [Ay) les deux côtés limites du terrain de monsieur Nakoué. Étant donnée une corde de longueur l, on veut trouver le point G, centre d’un cercle de rayon égal à l, tangent à la fois à [Ax) et à [Ay). »

Et aussitôt, sur le sol nu et de manière spontanée, il esquisse les croquis ci-dessous.

Figure 8 : Mathématisation d’un problème concret de nature agropastorale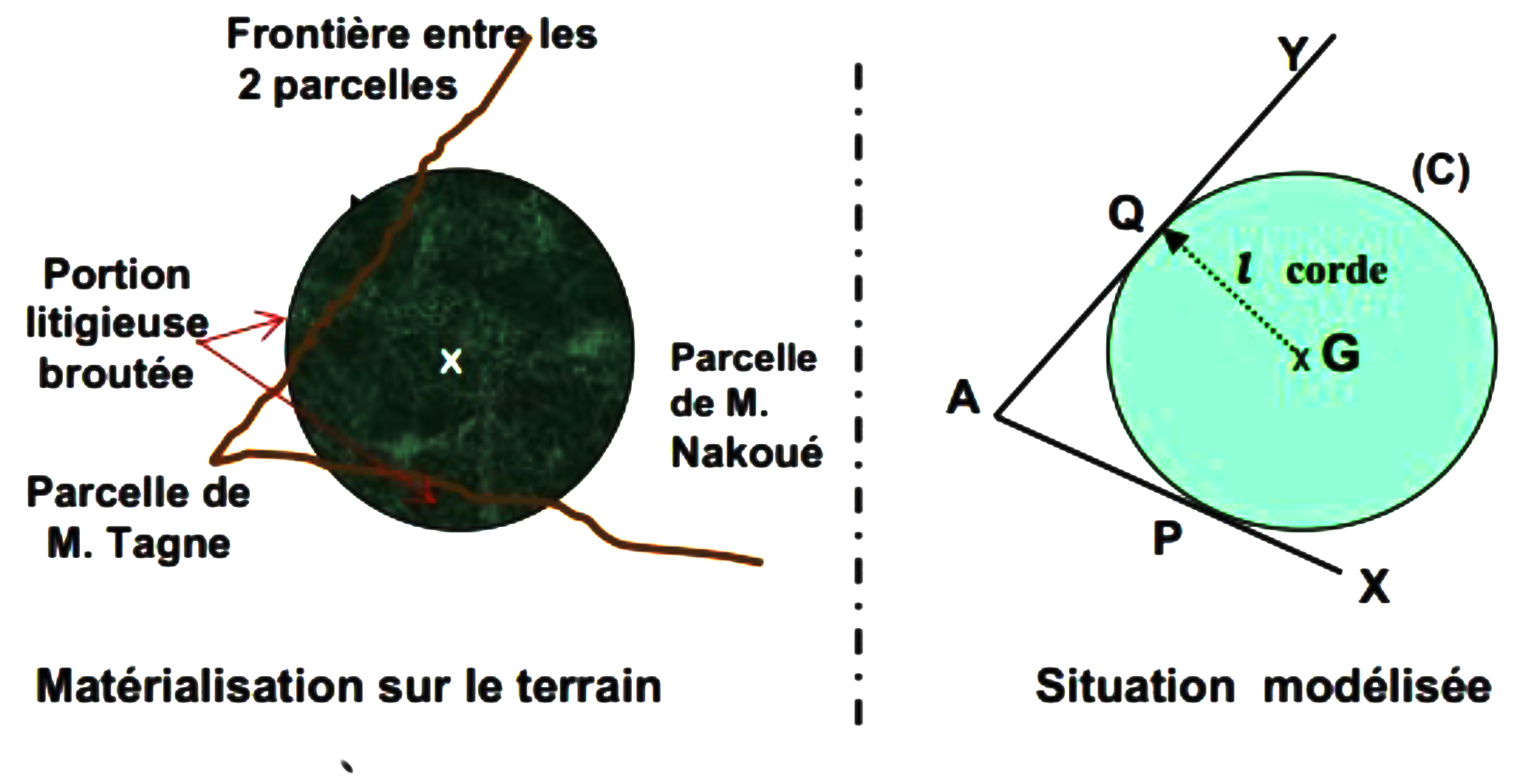

Notons G le centre du cercle (C), P et Q les points de contact de (C) avec les côtés limites [Ax) et [Ay) qui sont les frontières des deux champs et tels que GP = GQ = l où l = 7 m est la longueur de la corde, de sorte que et soient des angles droits. Puisque GP = GQ, on déduit que AP = AQ, d’après le théorème de Pythagore sur le triangle. Il conclut que le bon endroit pour fixer le piquet est le point G à équidistance de P et de Q, tel que GA = √AP²–l².

Ici, peuvent intervenir les notions de bissectrice d’un secteur, de médiatrice d’un segment, de tangente à un cercle et les propriétés de Pythagore. Par cette démonstration, nous voulions présenter le rôle décisif que peuvent jouer les mathématiques dans la résolution des problèmes des Africains au quotidien.

De nombreux exemples d’application des mathématiques en Afrique liés à l’héritage culturel africain existent dans la littérature (M’Backé Diop, 2009/2010/2011; Djebbar, 2015). Sans toutefois nous lancer dans les spécificités procédurales de ces applications, nous nous limitons à la présentation synoptique de quelques clichés. Pour ce faire, nous nous référerons à des périodes ayant précédé la colonisation. Il s’agit d’époques où les populations étaient encore sous-scolarisées et n’avaient pas encore connu l’influence de l’école occidentale ni celle des nouvelles technologies.

Le temps et l’apprentissage : de l’arithmétique à l’arithmosophie

Ici, deux aspects nous intéressent spécifiquement. Premièrement, le calcul du temps. Le temps de la journée était calculé par la longueur de l’ombre de l’objet qui varie du simple au double ou au triple, et dont la lecture permettait de fixer le temps de la journée pour honorer un rendez-vous ou pour mener une activité donnée. Le temps de la nuit était calculé par l’observation des étoiles, selon leur position par rapport aux points cardinaux et par rapport à d’autres astres.

Deuxièmement, le calcul simple ou l’arithmétique. Ce savoir était appris bien avant l’arrivée de l’école occidentale, à partir des livres écrits en langue arabe, par des auteurs et autrices de l’Afrique du Nord, notamment Abaa Maqra. Cette école était élitiste, car ceux et celles qui pouvaient l’enseigner étaient rares parmi les érudits, notamment les moodibbe^[33]. Cette science commençait par une étude des méthodes de calcul simple et rapide en utilisant des lettres de l’alphabet arabe appelé « Abjadia » et leur valeur chiffrée, en passant par la maîtrise d’un procédé complexe consistant à convertir des chiffres en lettres et vice-versa; et en même temps, procéder à la multiplication, la soustraction, l’addition et la division pour déboucher sur un résultat. Les opérations menées étaient marquées ou écrites sur du sable ou sur du papier. Dans les années 1960, les personnes qui pratiquaient avec aisance cette science étaient souvent sollicitées par des commerçants et commerçantes dans les marchés afin de les aider à faire les calculs nécessaires pour certaines transactions. D’ailleurs, on dit de ces personnes qu’elles étaient presque aussi rapides que la machine à calculer. Il convient de remarquer que la grande majorité de ceux et celles qui apprenaient et pratiquaient cet aspect des mathématiques ne s’arrêtait pas à ce niveau de compétence, mais évoluait pour devenir plus tard des numérologues, des arithmosophes^[34], des spécialistes en géomancie ou en horoscopie.

Le calcul de la zakat et la gestion de l’héritage : des solutions mathématiques à des obligations religieuses

Il y a bien longtemps que les mathématiques sont utilisées dans plusieurs aspects de la vie religieuse chez les musulmans en général et ceux du grand Nord-Kamerun en particulier. La zakat est une aumône légale obligatoire que chaque musulman devrait offrir annuellement aux personnes nécessiteuses lorsque ses biens atteignent une assiette, une masse ou un volume imposable à la zakat. Même s’il se passe qu’aujourd’hui encore dans certaines sociétés musulmanes d’Afrique et d’ailleurs, des disparités s’observent dans la mise en pratique de ce pilier de l’Islam, le principe religieux de son prélèvement ne souffre d’aucune opposition.

Les juristes musulmans ne s’accordent pas sur plusieurs aspects de la zakat. Chacun a ses propres opinions et arguments, et il y a parfois des contradictions qui laissent la majorité des populations dans le chaos et la confusion sur quelle opinion choisir^[35]. (Al Qaradawi, 2000 : xx)

Les biens économiques honnêtement acquis par tout·e musulman·e et susceptible d’être soumis à la zakat sont de divers ordres. On peut citer entre autres, les marchandises ou articles de commerce, les pierres précieuses (or, argent…), la fortune, les cheptels (chameaux, les bœufs, les brebis…), les produits agricoles, etc. Les détails techniques de calcul des différents ratios de la zakat selon les rubriques imposables citées précédemment sont présentés dans l’ouvrage d’Al Qaradawi (2000). Pour le cheptel bovin par exemple, et dans certaines conditions, la quantité imposable est de 30 bêtes ayant appartenu à son propriétaire pendant un an; et le taux d’imposition est d’une tête de bœuf d’un an révolu. Soit un taux de 1/30. Il faut noter que c’est le plus souvent à l’occasion du prélèvement de la zakat que le berger peul peut faire un dénombrement sérieux des bêtes de son cheptel, car par habitude, il est réputé connaitre ses bœufs et non leur nombre. En effet, dans son troupeau, il peut facilement remarquer l’absence d’une bête sans pour autant être capable de vous dire, en toute spontanéité et avec certitude, la taille de ce cheptel; paramètre auquel il accorde moins d’intérêt. Pour le capital de commerce et l’argent, le taux d’imposition est le ¼ du 10e tel qu’enseigné dans les livres de la législation islamique. En science moderne, ceci est exprimé en termes de pourcentage, soit 2,5 %. Chaque commerçant·e ou berger savait très bien comment faire l’inventaire de ses biens pastoraux et procéder, en toute honnêteté, au calcul et au prélèvement de l’imposition (la zakat). La taxe sur les produits agricoles (les récoltes), quant à elle, est calculée sur la quantité récoltée et non sur le poids des récoltes.

S’agissant de l’héritage avec les partages successoraux, il convient de noter que le Coran a prescrit les parts de biens à obtenir en héritage par certains ayants droit en termes de fraction.

Voici ce qu’Allah vous enjoint au sujet de vos enfants : au fils, une part équivalente à celle de deux filles. S’il n’y a que des filles, même plus de deux, à elles alors deux tiers de ce que le défunt laisse. Et s’il n’y en a qu’une, à elle alors la moitié. Quant aux père et mère du défunt, à chacun d’eux le sixième de ce qu’il laisse, s’il a un enfant. S’il n’a pas d’enfant et que ses père et mère héritent de lui, à sa mère alors le tiers. Mais s’il a des frères, à la mère, alors le sixième, après exécution du testament qu’il aurait fait ou paiement d’une dette. De vos ascendants ou descendants, vous ne savez pas qui est plus près de vous en utilité. Ceci est un ordre obligatoire de la part d’Allah, car Allah est, certes, Omniscient et Sage. » (Coran en ligne, Sourate 4 An-Nisa’a – Les femmes : verset 11)^[36]

Il y a donc parmi les ayants droit à l’héritage, ceux qui bénéficient de la moitié (½), du tiers (1/3), du quart (¼), du sixième (1/6) ou du huitième (1/8) des biens du défunt. Lorsqu’il faut partager ou redistribuer ces différentes fractions aux ayants droit, il faut trouver, entre autres, le dénominateur commun, afin de déterminer avec toute la précision recommandée par le Coran, la part exacte de biens qui devrait revenir à chacun, avant de passer au partage proprement dit. Cette procédure concernant les partages successoraux n’est pas normalisée à tous les cas. Il y en a d’autres selon les spécificités liées aux relations filiationnelles avec le défunt qui s’inscrivent dans l’ordre générationnel dont le bénéficiaire est tributaire. Cependant, bien que cette procédure soit assez complexe pour ceux qui n’ont pas été à l’école occidentale, il faut remarquer que dans les sociétés traditionnelles musulmanes, les calculs ont toujours été effectués, avec succès, par l’une ou l’autre parmi les compétences religieuses locales, notamment l’Akaali^[37], grand juge du lamidat^[38] (petit territoire musulman au Nord-Kamerun), le lamido (chef politique et spirituel d’un lamidat) lui-même, un érudit ou un imam (guide spirituel et temporel d’une communauté islamique).

Par ailleurs, dans notre volonté de dévoiler les mathématiques dans les activités humaines au quotidien, il faut observer que certaines propriétés ou théorèmes mathématiques, au-delà de leurs fonctions premières comme outils mathématiques, ont des interprétations qui sont en adéquation avec la réalité de certaines situations de vie. On peut s’intéresser à certains d’entre eux.

(a) « Le théorème des gendarmes » pour le calcul des limites de certaines fonctions numériques

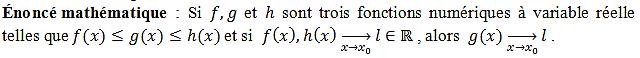
Cet outil permet de calculer la limite de certaines fonctions par encadrement.

Interprétation à travers un fait de société :

Si  g désigne un coupable, f et h deux gendarmes qui en tout temps « x » encadrent le coupable g, « f(x) ≤ g(x) ≤ h(x) », en le tenant par ses bras gauche et droit respectivement. Si à un moment donné « x → x₀ », les deux gendarmes se dirigent vers une même et unique porte :

Les propriétés (b1), (b2) et (b3) peuvent être interprétées de la manière suivante :

• (b1) : Si les enfants et la nation émergent à travers une saine éducation alors les parents et le gouvernement s’en réjouiront et émergeront pareillement à travers un développement multisectoriel irréversible.
• (b2) : Si les parents et le gouvernement sombrent dans la normalisation des écarts en fuyant devant leurs responsabilités régaliennes, alors les enfants et la nation sombreront pareillement dans les déviances civiques et morales.
• (b3) : Si les parents et le gouvernement se compromettent dans le tribalisme et la grande corruption, alors les enfants et la nation feront pareillement à travers la tricherie et la haine tribale.

Il s’agit là de quelques situations de vie plausibles en Afrique qui, dépouillées des incertitudes liées à l’ondoyance et la versatilité des comportements des êtres humains, épousent les modèles mathématiques précités, avec un degré de corrélation élevé. En effet, cette présentation quelque peu sommaire dévoile comment les mathématiques, à travers ses outils et ses résultats, peuvent être à l’usage perpétuel des hommes et des femmes dans la prise de certaines décisions pour la gestion de la cité pourvu que l’on s’appuie sur ses praticien·ne·s.

Ces récits comme beaucoup d’autres récits s’originent dans le vécu des populations africaines. Ils montrent à suffisance que l’utilisation des mathématiques n’est pas étrangère à leurs pratiques ou à leurs activités. Puisque la question des preuves de la pratique des mathématiques dans les sociétés africaines est aujourd’hui dépassée, celle qui est capitale à présent c’est celle de savoir quelles mathématiques sont nécessaires pour le développement de l’Afrique. Si pour accéder au développement, il est nécessaire de créer des industries et de nouvelles technologies, il est sans doute aussi utile que l’épanouissement des populations africaines, des plus petites aux plus grandes, s’opère par la résolution de leurs problèmes à l’échelle locale, puis globale. Les interactions entre les humains, l’espace, les animaux et l’école sont courantes en Afrique. Les rationaliser par le biais des modèles mathématiques, appris à l’école ou en dehors, est une solution efficiente et durable, une voie par excellence d’accès aux mathématiques pour le développement^[39].