2 Quelques fondamentaux épistémologiques de l’enseignement des mathématiques
Les élèves doivent acquérir des connaissances à la fois théoriques et pratiques ainsi que des éléments d’une véritable culture scientifique grâce à une initiation à la philosophie et à l’histoire des mathématiques ainsi qu’à leur rôle dans l’évolution du monde. (Touré, 2002 : 177)
Une réflexion profonde sur la nature, les principes et les motifs de l’enseignement des mathématiques peut permettre de contrer le flux des idées rétrogrades, préconçues et véhiculées par certains individus à propos de cette discipline. Des débats et discussions philosophiques entre pairs, membres d’une même communauté ou groupes de recherche, il ressort que les mathématiques sont davantage perçues comme des instruments, des outils de raisonnement ou comme un simple langage conventionnel commis pour la construction d’une société humaine en perpétuelle évolution, et non comme une science fermée et inaccessible au premier venu (Popper, 1999; Lecourt, 2015; Bachelard, 2015 [1969]). Ce chapitre a pour objectif de mener une réflexion philosophique sur les mathématiques pour mieux les situer dans leur contexte propre (Pallascio, Daniel, Lafortune & Sykes, 1996) d’un triple point de vue : la définition de la discipline, la description des principes qui gouvernent son raisonnement et les buts recherchés par son enseignement.
Nous allons passer en revue les conceptions de quatre philosophes : Platon, Descartes, Bachelard et Kant, à propos de la définition des mathématiques. Nous verrons de manière subséquente que cette définition est susceptible de connaitre des ajustements au gré de l’évolution de la recherche. Notre point de départ sera un tableau global des différentes sciences, en faisant ressortir la position spécifique des mathématiques dans l’univers du savoir. Ensuite, nous rappellerons les principes fondamentaux et, enfin, nous présenterons les objectifs généraux de l’enseignement de cette discipline.
De la connaissance épistémologique en mathématiques et son impact sur les pratiques enseignantes
De nombreux jeunes scolarisé·e·s et postscolarisés pensent ou jugent les mathématiques au travers de l’image de leurs enseignant·e·s qui sont, dans certains cas, dispersé·e·s et négligé·e·s, et dans d’autres, entièrement absorbé·e·s par leurs sujets, en rupture avec le monde réel, et n’ayant pas de vie personnelle à l’extérieur des mathématiques. Dans la société en général, cette vision stéréotypée semble persister. Nous savons pourtant combien la relation élève-enseignant·e est déterminante dans la réussite scolaire de l’élève. Les enquêtes réalisées par Poirier, Lessard, Fortin & Yergeau (2013) auprès de 756 élèves du secondaire au Québec ont montré la forte corrélation entre l’attitude de l’enseignant·e et le décrochage scolaire. Ainsi, une relation cordiale et bienveillante entre l’enseignant·e et l’apprenant·e a le mérite de réduire le risque de décrochage scolaire, voire l’intention de décrocher. En corrélant la relation élève-enseignant·e avec les variables telles que l’âge, la réussite et l’absentéisme, les auteur·e·s parviennent à montrer que l’attitude de l’enseignant·e envers l’élève est le facteur le plus significatif parmi les causes du décrochage qu’il soit du fait de l’âge ou des performances. Le risque de décrochage le plus élevé (soit un score de 90,07) trouve sa source dans cette attitude. Cette évaluation repose sur l’appréciation de la qualité de la relation élève-enseignant·e que les auteur·e·s articulent en cinq variables : l’engagement de l’élève, le soutien de l’autonomie, l’encadrement, l’implication émotionnelle, les attitudes de l’élève envers l’enseignant·e (Poirier, Lessard, Fortin & Yergeau, 2013 : 12-13).
On constate régulièrement que les individus qui croient ne pas pouvoir réussir en mathématiques détestent systématiquement cette discipline; gardant simplement le complexe d’incapacité pendant très longtemps. En revanche, ceux et celles qui semblent s’en sortir mieux laissent paraître beaucoup d’insuffisance en matière de principes élémentaires des relations sociales ou de vie en communauté (Vergnaud, 1982). Cette représentation, tout en indiquant les défauts à reprocher aux mathématicien·ne·s (enseignant·e·s, chercheur·se·s), reste erronée et reflète des clichés factices des mathématiques, très souvent limités à tort au calcul de nombres, de distance et à l’arithmétique de base.
En regardant de plus près et en toute rigueur, il faut avouer que le problème du statut et de la réception des sciences mathématiques par les jeunes est lié à leur définition même, leur nature, ainsi que leurs méthodes d’enseignement-apprentissage-expérimentation. Les mathématiques sont-elles une réalité objective reflétant la structure du réel, et même de l’être, ou bien sont-elles le simple reflet de l’esprit du mathématicien ou de la mathématicienne qui les crée ? Ces questions épistémologiques ne sauraient être éludées si l’on veut s’inscrire dans une démarche de démystification des mathématiques. Elles vont permettre de lever un pan de voile sur ce que certains pensent être le « mystère » des mathématiques, ou encore ce que Srinivasa Rao (2000) appelle « mathémagie » [1].
Définition et taxonomie des branches des mathématiques
Si l’usage des outils mathématiques dans différentes sciences, ainsi que son enseignement et sa pratique sont répandus, sa définition comme science n’est pas toujours clairement cernée par tous ceux/celles qui s’y intéressent. Il est donc nécessaire de répondre à deux questions essentielles : qu’est-ce que les mathématiques? Quelles en sont les branches, les approches et les théories?
Approche définitionnelle des mathématiques
Le terme « mathématique » est issu du mot grec « mathêmaticos », puis du mot latin « mathematicus » (Dauzat, Dubois & Mitterand, 1971 : 451). On peut le décomposer en deux éléments : d’une part mathêma, « science » formée sur la racine, c’est-à-dire un substantif du verbe « manthênein » qui signifie « apprendre » (Dauzat, Dubois & Mitterand, 1971 : 451); d’autre part, le suffixe d’origine grecque « -tique » que l’on retrouve dans les noms des arts, des techniques, des méthodes, des styles (Traoré & Barry, 2007). La mathématique est donc définie comme suit :
La mathématique est une science hypothético-déductive qui, en développant un langage autonome, élabore et étudie des notions abstraites liées les unes aux autres et souvent capables de fournir des modèles et des processus opératoires permettant de mieux comprendre de nombreux aspects du monde observable, en particulier lorsque peuvent être invoquées des idées de quantité, de forme et de partie de quelque chose. (Pruvost-Beaurain, 2019)
Autrement dit, les mathématiques sont la science qui étudie les nombres, l’espace ainsi que les structures qu’elles créent elles-mêmes pour leurs propriétés et l’analyse de leurs modèles. En d’autres termes, elles sont cette matière enseignée à l’école qui permet d’étudier l’algèbre, l’arithmétique et la géométrie. En somme, les mathématiques désignent l’ensemble des théories concernant les nombres, les figures géométriques, les structures algébriques et topologiques, les fonctions numériques et complexes, le calcul intégral et différentiel, les probabilités et statistiques, les ensembles…
C’est ainsi qu’on distingue en les classifiant, les théories mathématiques pures ou fondamentales et les théories mathématiques appliquées (Guillopé, Helffer, Pansu & Prural, 1998). Les origines lointaines de ces deux grandes branches des mathématiques (endogène et exogène) somme toute interdépendantes, selon Anta Diop, proviennent de l’existence de « deux écoles de pensée correspondant aux deux courants philosophiques, idéaliste et matérialiste, même si l’appartenance des scientifiques à ces écoles n’est pas toujours explicitement avouée. » (2011 : 163). Il reste que, au fil des années, ces deux grandes tendances ont connu un développement tel qu’il en a découlé une multitude d’approches, des théories au sein de chacune des branches.
Typologie des approches en mathématiques
Dans la pratique, il existe de nombreuses conceptions mathématiques. Mani (2007) distingue trois aspects sous lesquels le savoir mathématique peut être perçu : un aspect interne aux mathématicien·ne·s, un aspect social et un aspect culturel. Pour lui, les mathématiques pures (« pure mathematics ») doivent être considérées comme un corps d’idées qui émergent et qui se logent dans l’esprit des mathématicien·ne·s :
Les mathématiques pures sont un immense organisme construit entièrement et exclusivement sur des idées qui émergent dans l’esprit des mathématicien·ne·s et y vivent.[2] (2007 : 1)
L’auteur, pour expliquer sa définition, trace trois trajectoires pouvant être empruntées par le mathématicien ou la mathématicienne. Premièrement, les mathématiques peuvent être conçues comme les résultats ou les contenus des publications des chercheurs et des chercheuses (manuscrits, livres, articles scientifiques, notes de cours, etc.). Ensuite, une autre conception consiste à considérer les mathématiques comme une activité humaine profondément ancrée dans la réalité (« deeply rooted in reality »). Enfin, vient en troisième position ce que l’auteur nomme « château des mathématiques » (« castle of mathematics »), désignant ainsi, le niveau le plus élevé dans l’abstraction mathématique, comme un étagement supérieur (« towering somewhere in the Platonic World of Ideas ») (« dominant quelque part dans le monde platonique des idées ») surplombant les autres.
Cette branche comprend d’une part les théories mathématiques de la quantité et d’autre part celles de l’ordre. Parmi les sciences mathématiques de la mesure ou de la quantité, on distingue :
-
les théories mathématiques complexes du nombre et de l’espace travaillent sur l’analyse infinitésimale, la géométrie différentielle, le calcul intégral, le calcul des probabilités, la géométrie analystique, etc.;
-
les théories mathématiques du nombre qui s’ouvrent à l’arithmétique, l’algèbre élémentaire et abstraite, la théorie des nombres (entiers, relatifs, rationnels, réels). Les chiffres/symboles de zéro (noté « 0 ») à neuf (noté « 9 »), sont d’origine indo-arabe et adoptés par les mathématicien·ne·s d’Occident grâce à Gerbert d’Aurillac et Leonardo Fibonacci. C’est à ce dernier que l’on attribue le mérite de les avoir répandus en Occident à travers son ouvrage Liber Abaci, traité d’arithmétique publié en 1202 et qui prône les avantages des méthodes de calcul des pays de l’Islam, notamment la méthode positionnelle indienne (Bouslama, 2006; Greenwald & Thomley, 2012 : 54).
La diffusion en Occident des chiffres arabes[3] a permis d’établir un nouveau système d’écriture des nombres. Cette écriture facilite la formulation de règles pour les opérations et de conventions de calcul qui rendront possible, à partir du XVIe siècle, l’invention de l’algèbre. L’entier naturel, dans sa plus ancienne idée « proto-mathématique rigide » 1, 2, 3… est telle que ces premiers entiers ont acquis des significations symboliques, et mêmes religieuses dans plusieurs cultures. Cette idée est devenue « protophysique » avec le comptage des objets matériels et plus tard des objets immatériels comme le temps (avec les jours et les nuits…). Cette idée est devenue « mathématique » quand il a fallu compter, additionner ou faire du commerce. Un système numéral universel (le système décimal) a été inventé. Un siècle plus tard, après l’invention de l’algèbre, la création de la géométrie (analytique) et l’introduction de l’idée de fonction, naîtront diverses sous-branches des mathématiques comme le calcul infinitésimal (l’analyse comprend le calcul différentiel et le calcul intégral) ou le calcul des probabilités (Greenwald & Thomley, 2012 : 806).
- la théorie des groupes, la topologie, la théorie des ensembles et la logique mathématique se développeront pour l’essentiel à partir du XIXe siècle. La théorie des groupes avec Évariste Galois traite d’ensembles munis d’une loi de composition interne vérifiant certaines propriétés spéciales. Les théories mathématiques de l’espace intègrent les différentes géométries (affine et projective) : la géométrie euclidienne et les géométries non euclidiennes (de Lobatchevski ou de Riemann). La topologie avec Riemann s’intéresse aux propriétés mathématiques « invariantes » par déformation géométrique ou par transformation « continue » des objets. Lorsqu’un espace est courbé, tordu, étiré ou plus généralement déformé, certaines propriétés mathématiques demeurent inchangées.
Parmi les sciences mathématiques de l’ordre, on distingue :
-
la théorie des ensembles avec Cantor. Elle a permis notamment de définir avec plus de précision le concept d’« infini »;
-
l’algèbre, de l’arabe al-jabr, « contrainte, résolution », est la branche des mathématiques qui étudie la résolution d’équations à l’aide des signes et symboles (algèbre classique) ou à l’aide de structures mathématiques comme les groupes, les anneaux et les corps (algèbre universelle). D’après Masood, l’algèbre, par la diversité de ses développements et la contribution des chercheur·se·s, compte parmi les composantes les plus importantes des mathématiques :
De plus, avec l’algèbre d’Al-Khwarizmi, ces savants nous ont fourni le plus important outil mathématique jamais conçu, et qui sous-tend toutes les facettes de la science, ainsi que des processus plus quotidiens.[4] (2009 : 139-140)
Ainsi, pour l’auteur, l’algèbre est considérée comme l’un des plus grands outils mathématiques jamais inventés, qui, à travers son usage, rejoint presque toutes les autres branches de la science. Al Khwarizmi écrit le premier traité d’algèbre sous le titre Abrégé du calcul par la restauration et la comparaison[5]. La latinisation du nom de ce mathématicien a donné naissance au mot « algorithme ». Par ailleurs, ce livre constitue une somme d’informations considérables sur la résolution des équations de premier et de second degré et il ne contient aucun chiffre, toutes les équations étant écrites avec des mots.
- la théorie des catégories, introduite au début des années 1940 par Samuel Eilenberg et Saunders MacLane, est comme un langage pour étudier les structures mathématiques et les relations qu’elles entretiennent.
Aussi rigoureuse qu’une telle conception puisse être, elle nous laisse cependant dubitatifs quant à son efficacité. Dire qu’il est un niveau supérieur de la pratique mathématique induit que les autres niveaux sont inférieurs. Dire que les mathématiques pures constituent le summum de la réflexion mathématique, c’est considérer que des pratiques d’une mathématique ancrée dans la réalité ou contextualisée seraient secondaires. Nous ne partageons donc pas cette conception hiérarchisée des pratiques mathématiques qui peuvent mener à des discriminations, à des injustices cognitives. Nous pensons que toutes les disciplines mathématiques sont dignes d’intérêt qu’il n’y a pas lieu d’en faire une hiérarchie. Sans amoindrir le rôle que peuvent jouer les mathématiques dites « pures » dans le développement de l’intellect et de la cognition humaine, nous privilégions, dans nos pratiques, une approche mathématique qui se préoccupe des conditions de vie des populations. Ce sont donc des mathématiques au service du développement humain dont il s’agit. Comment concevoir autrement la place d’une discipline aussi centrale dans la vie humaine quand on est membre d’une société où les besoins parmi lesquels les plus élémentaires manquent? Peut-on, à juste titre, se satisfaire d’une course vers le « château des mathématiques » alors que la majorité ne possède ni les moyens d’accéder au château ni la possibilité de le voir et de le toucher. Par cette analogie, nous voulons montrer que les besoins humains, aussi minimes soient-ils, ne sauraient être détachés des préoccupations intellectuelles, car si faire de la science pour la science est bien, faire de la science pour le progrès est meilleur. Piron nous invite à nous poser les questions suivantes : quel rôle une université peut-elle jouer dans le développement local durable de la communauté qu’elle dessert (ville, région, pays), elle dont la vocation est officiellement de transmettre des connaissances « scientifiques » de type universel? Qu’a-t-elle à dire et à faire à propos des enjeux du développement local de sa communauté? (Piron, 2016 : 308).
En réfléchissant à ces interrogations et en les mettant en relation avec l’environnement dans lequel nous vivons (ville de Ngaoundéré, région de l’Adamaoua au Kamerun), on voit jaillir tout de suite les problèmes vécus par la population au quotidien, et surtout les solutions que peuvent apporter les mathématicien·ne·s: les infrastructures scolaires, les infrastructures routières, les infrastructures sanitaires, la gestion de la circulation, la gestion des marchés, l’urbanisation, l’approvisionnement en eau et en électricité, la gestion des déchets ménagers, etc. On se rend compte qu’il n’y a pas un secteur de la vie qui ne puisse être l’objet d’une investigation mathématique. Il suffit d’y penser. Dans le cas de la circulation urbaine par exemple, les systèmes dynamiques peuvent être mis à contribution pour évaluer le flux de la circulation, le repérage des endroits à forte densité de circulation et les horaires de pointe. Dans le cas de la gestion domestique du revenu familial, les systèmes d’équations ou d’inéquations linéaires peuvent aider à gérer le type de rationnements spécifique ou sous contraintes de l’alimentation de la famille. D’autres exemples de solution dans d’autres secteurs peuvent être envisagés. C’est de cette manière que nous pourrons réconcilier les mathématiques, voire la recherche scientifique, avec la société; en réduisant significativement l’écart entre l’univers des mathématiciens·ne·s et le monde des profanes. On aura aussi contribué à résorber cette image mystifiante de la discipline.
Les théories mathématiques appliquées s’intéressent, de leurs côtés, aux applications des savoirs et aux résultats des mathématiques fondamentales dans d’autres disciplines. C’est ainsi qu’on parle souvent de mathématiques pour les sciences de l’ingénieur, pour biologistes, entre autres. Ses activités sont essentiellement à caractère exogène, c’est-à-dire portées vers l’utilisation des outils et démarches mathématiques pour répondre à des préoccupations en dehors du domaine des mathématiques pures comme en ingénierie, en économétrie, en météorologie, en épidémiologie, en statistiques, en théorie des jeux, en mécanique, en physique, en chimie, en biologie, en linguistique, en sociologie, en littérature, en politique…
En général, les outils des mathématiques (pures ou appliquées) peuvent être sollicités pour mener des études approfondies sur des phénomènes ou les situations observées, vécues ou non par les humains. L’un des principes éthiques de cet usage est que ces outils doivent contribuer à la réalisation du bonheur des humains et non le contraire. C’est à ce titre que Rabelais met en garde les esprits crédules qui font la recherche pour la recherche en rappelant, à toutes fins utiles, que « Sapience n’entre point en ame malivole, et science sans conscience n’est que ruyne de l’ame »[6] (Rabelais, 1992/1993 [1532] : 31). Cette règle qui rappelle la nécessité d’une pratique moralement saine de la science ne se limite guère aux discours du scientifique. Elle concerne aussi ses objectifs, son mode de raisonnement et sa démarche.
Réflexion philosophique sur la scientificité des mathématiques
Qu’on les situe dans la Grèce antique (Bouveresse, Itard et Sallé, 1977), dans l’Égypte pharaonique, dans le bassin du Congo (Huylebrouck, 2005) ou dans la civilisation asiatique (Dahan-Dalmédico & Peiffer, 1982), les mathématiques ont toujours fait figure de modèle dans la recherche de la vérité scientifique (Baumann, 2004-2005; Launay, 2016). Les philosophes tels que Platon, Descartes, Spinoza et Leibniz en font l’outil idéal de la science, de la connaissance, le chemin privilégié vers la philosophie. Les réflexions philosophiques de ces auteurs se rapportent généralement sur la scientificité des mathématiques : quels sont l’objet, les méthodes et la finalité de cette discipline?
La conception platonicienne : la mathématique comme outil de préparation à la dialectique
Platon a fait inscrire au fronton de son école, dans les jardins de l’Académie qu’il a fondée en 387 avant Jésus-Christ (Brisson, 2014) la formule suivante : « que nul n’entre ici s’il n’est géomètre ». Cette injonction indique, à n’en point douter, qu’avant de s’intéresser à la philosophie, il faut se mettre d’abord à l’école de la science des figures et de l’espace physique, qui de nos jours est considérée comme une branche mathématique. Pourquoi faut-il être géomètre? Autrement dit, pourquoi faut-il être doté des connaissances en géométrie pour accéder à l’école platonicienne? Posséder les connaissances en géométrie sous-entendrait alors que l’on soit doué de raison, doté du bon sens et imprégné d’idées de logique procédurale[7]. En effet, Platon dans La République affirme que la géométrie « a pour objet la connaissance de ce qui est toujours et non de ce qui naît et périt » (trad. de Baccou, 1936; Kindschi, 2005). La notion de connaissance et notamment de connaissance vraie si chère à Platon est possiblement accessible par l’esprit humain dans le domaine de la science du réel contrairement à la vision pessimiste de certains présocratiques comme Xénophon, Parménide et Démocrite, qui trouvent que « l’homme ne peut pas atteindre la vraie connaissance, selon eux, mais seulement formuler des opinions, affirment-ils. La vérité n’est accessible qu’aux dieux. » (Drouet, 2020 : 1-2). Cependant, tous partagent le schéma épistémo-ontologique qui oppose les apparences sensibles à la réalité, et l’opinion au savoir. Dans le livre VI, Platon montre d’une manière subtile la position et l’importance de la science et notamment de la ou des mathématique·s dans le vaste univers des formes de savoirs. Pour ce faire, il utilise le fameux symbole de la ligne pour développer conjointement et par une analogie remarquable, la théorie de l’Être (Ontologie) et la théorie de la Connaissance (Épistémologie). C’est d’ailleurs dans cette dernière théorie qu’il situe la ou les science·s et avec elle·s, la ou les mathématique·s.
L’allégorie de la ligne de Platon
Platon représente sous la forme d’une ligne verticale segmentée (voir dessin ci-dessous proposé par Yvon Lafrance, 1981, 159-196), les différents degrés de connaissance ou formes de savoirs selon leurs objets et leurs rapports de démarquage respectifs.
Figure 2 : Schéma de l’allégorie de la ligne : AC : CB = AD : DC = CE : EB (d’après Y. Lafrance, 1981).
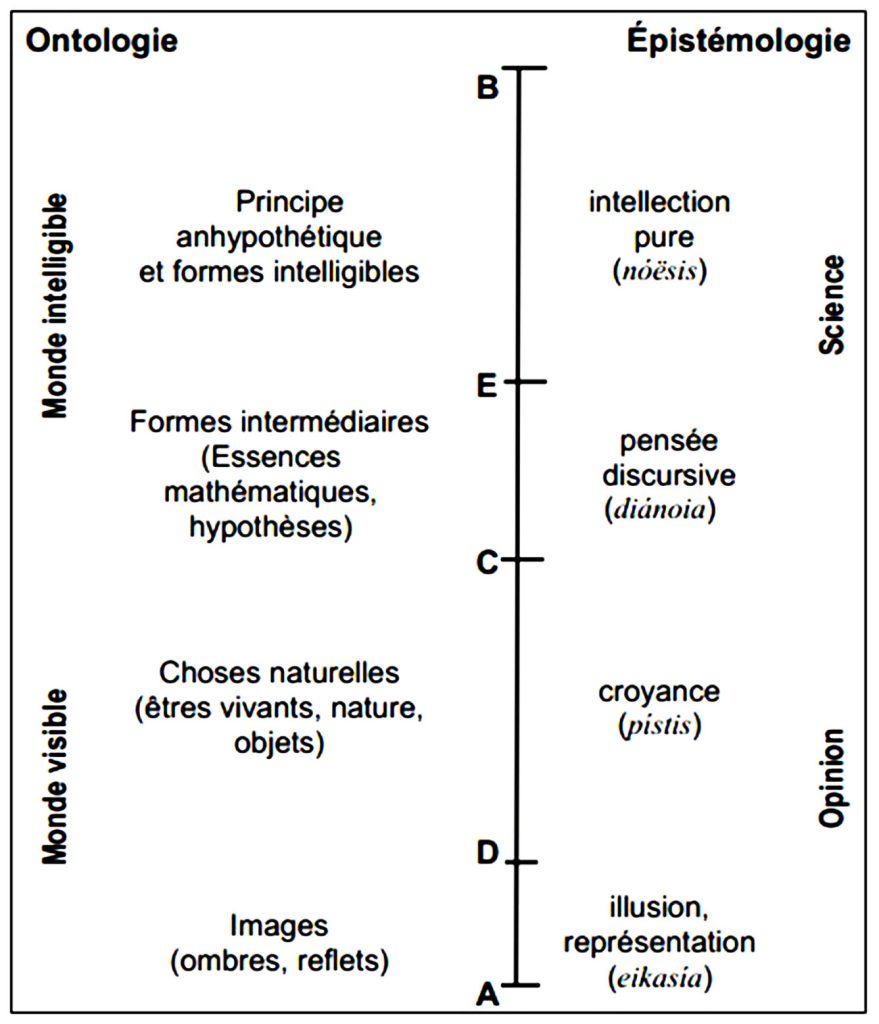
Dans sa démarche, il commence par tracer une ligne verticale segmentée et orientée (du bas vers le haut marquée (AB), qui divise l’espace en deux demi-plans (côtés gauche et droit) dont l’un (côté gauche) représente la théorie de l’être (Ontologie) et l’autre (côté droit) représente la théorie de la connaissance (Épistémologie). Puis il coupe horizontalement par un point marqué C, cette ligne en deux parties. Une des moitiés dans le demi-plan Ontologie représente le genre ou le monde visible et l’autre le genre ou monde intelligible. Dans le demi-plan Épistémologie et selon le même ordre de progression, une des moitiés représente l’opinion et l’autre moitié représente la science. Il coupe de nouveau horizontalement en deux parties aux points marqués D et E respectivement, les moitiés en dessous de C et au-dessus de C, de sorte que les proportions AC : CB = AD : DC = CE : EB[8] soient toujours gardées. La première moitié du monde visible représente les ombres et les images des objets matériels et la seconde moitié de ces objets eux-mêmes. La première moitié du monde intelligible représente les formes intermédiaires et la seconde moitié représente les formes intelligibles. La première moitié de l’opinion représente les illusions ou représentations que nous avons des choses sensibles et la seconde moitié représente la croyance naïve. La première moitié de la science que nous avons des choses intelligibles représente la pensée discursive et la seconde moitié l’intellection pure ou la dialectique. Pour Platon, nos opinions sont l’équivalent des images parfois trompeuses que nous constatons dans le monde visible. Par exemple, quand le soleil frappe sur notre tête, nous avons l’impression qu’il est juste au-dessus de nous, et pourtant, il se trouve à des années-lumière de la terre, alors que notre science représente les objets eux-mêmes dans le genre ou monde intelligible.
Ce schéma de Lafrance (1981) reste très laconique et ne nous permet pas de situer clairement la position de la ou des mathématique·s dans le genre/monde intelligible.
Drouet décrit cette analogie de la ligne de Platon par une approche dualiste comparée qui nous semble plus aisée à la compréhension, et qui rend plus « visible » la position de la ou des mathématique·s en épistémologie :
On retrouve ici le même principe d’organisation que précédemment : les objets de la connaissance déterminent, par leur nature spécifique, les degrés de la connaissance.
– Au genre des objets visibles correspond l’opinion;
– Au genre des objets invisibles (intelligibles) correspond la science.
Chaque genre d’objet et chaque degré de connaissance se subdivise à son tour :
– Les objets visibles (ou sensibles) sont soit des images soit des choses sensibles. Les images ne peuvent être connues que par l’imagination, laquelle ne produit que des représentations ou des illusions. Les choses sensibles ne peuvent donner lieu qu’à des certitudes sensibles, des croyances (pistis). Dans les deux cas, on n’a affaire à une connaissance obscure, instable et faillible (l’opinion) précisément, car son objet est sensible, instable, toujours autre que lui-même.
– Les objets invisibles (ou intelligibles) sont soit les objets mathématiques et les hypothèses soit les formes intelligibles. Les objets mathématiques sont connus par la pensée discursive ou dianoétique (dianoia), qui procède par des démonstrations, lesquelles sont des discours (raison pour laquelle les démonstrations appartiennent au genre de la pensée discursive). Les formes intelligibles, quant à elles, ne peuvent être appréhendées que par la pensée intuitive ou noétique, donc par-delà le discours, sous la forme plutôt d’un contact direct (le plus souvent présenté comme une vision) avec la réalité. Seule la vision des formes intelligibles peut donner lieu à une connaissance parfaitement claire.
À chacun de ces degrés se rattachent toutes les disciplines d’éducation des gardiens de la cité décrites dans la République.
– À l’imagination correspondent la musique et la poésie. En proposant des images de la vertu et du vice, les arts participent de l’éducation. Pour reconnaître la beauté et toutes les vertus dans les belles choses de l’art, l’âme doit d’abord en avoir reconnu les formes. En retour, à défaut de savoirs, les arts donnent de bonnes habitudes à l’âme, la mettant dans un état d’harmonie […].
– À la certitude sensible et aux croyances qui en découlent correspond la gymnastique. En s’occupant du corps, la gymnastique focalise l’attention de l’âme sur ce qui naît et ce qui meurt […].
– Aux sciences mathématiques correspond l’exercice de la pensée discursive proposé par l’arithmétique, la géométrie, l’astronomie, la stéréométrie[9] et l’harmonie […].
– Enfin, la pensée intuitive est exercée par la dialectique.
Platon semble ainsi désigner trois grands degrés de connaissance pour l’homme :
– La connaissance sensible
– La connaissance mathématique
– La connaissance dialectique, réservée au seul philosophe.
L’idée directrice que semble poursuivre Platon ici est que la philosophie se distingue des autres modes de connaissance : en tant qu’elle est la science par excellence, elle rend l’esprit capable de se ressouvenir des formes intelligibles qui donne l’explication de toutes choses. Elle rend également capable de se détacher du corps et du sensible, pour ne s’en tenir qu’à la pensée pure. Le philosophe est donc le seul à pouvoir saisir l’être des choses, par le seul exercice de la pensée dialectique.[10] (Drouet, 2020 : 10-11).
Cette explication de Drouet (2020) nous permet à suffisance de résumer, à notre manière, l’allégorie de la ligne de Platon à travers l’illustration schématique ci-après, dans laquelle les parties issues des subdivisions successives respectent bien le même rapport dimensionnel de proportionnalité et sont hiérarchisées en niveaux (1er niveau et 2e niveau), aussi bien dans le monde réel que dans le monde non réel, et suivant le degré de perception des réalités par nos sens et par notre esprit. Les termes dia noya et dianoia (utilisés par Drouet) représentent pour nous cette même entité intelligible qui, à travers la pensée discursive, saisit les objets mathématiques et procède toujours par une démarche démonstrative pour rechercher la vérité. Le mot « Science » avec un « s » majuscule n’est pour nous qu’une illustration de la grande famille des disciplines reconnues sans complaisance comme scientifiques.
Figure 3 : Position de la ou des mathématique·s dans l’univers des savoirs
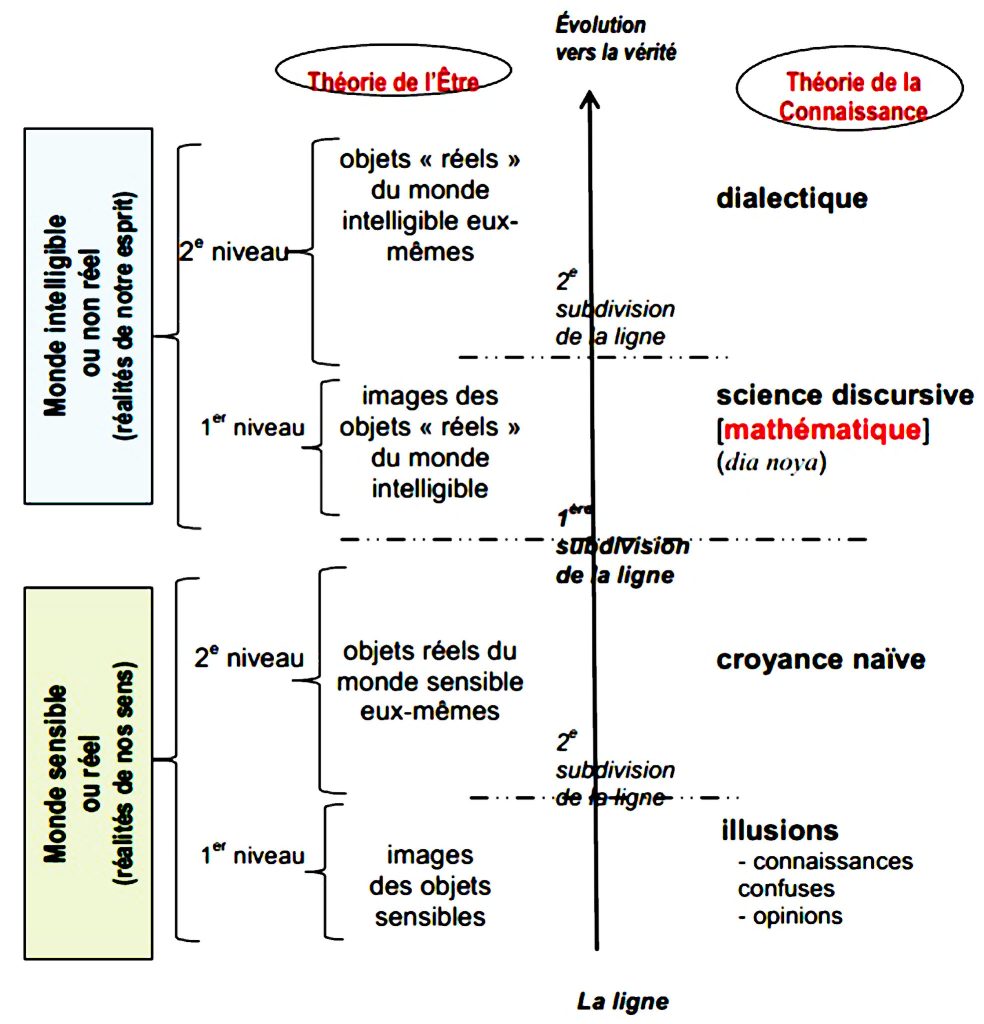
L’esprit humain possède des principes, des idées naturelles, dont des notions mathématiques. Les rationalistes soutiennent que ces notions mathématiques existent a priori, indépendamment de toute expérience. Par exemple, les opérations de comptage et d’addition avec les nombres entiers naturels ne sont l’objet d’aucune abstraction humaine. Elles se trouvent dans les actes marchands traditionnels, le dénombrement de bétails et les mesures agraires des sociétés humaines. Par contre, certains concepts mathématiques créés à une époque passée semblent avoir été abandonnés faute d’intérêt pour les chercheur·e·s (Dyson, 1972). De l’avis de Platon, il existe un monde des idées fait de réalités intelligibles qui sont des modèles de choses sensibles. Il postule que le monde sensible est une copie pâle du monde intelligible qui seul est véritablement réel [trad. de Baccou (1936)]. Le premier, dans la mesure où il est soumis au mouvement, au devenir, à la corruption, à la justice humaine (essentiellement non-distributive et en proie à la subjectivité) n’est pas un monde susceptible de donner lieu à la connaissance parce que tout est en devenir, tout est apprécié par nos sens. La connaissance, sans être immuable pour ce philosophe, s’occupe de ce qui est stable, ce qui ne se transforme pas, ce qui ne varie pas, et en un mot, ce qui est immuable.
Pour Platon, les mathématiques se situent au premier niveau du monde intelligible dans la théorie de la connaissance[11]. Elles sont intermédiaires entre les deux mondes sensible et intelligible. L’effort philosophique consiste à se débarrasser des apparences pour accéder à l’Être, pour le connaître tel qu’il est. Les mathématiques aident déjà dans ce sens. Les mathématicien·ne·s raisonnent sur les objets tels que le cercle, la ligne, le point, le carré, l’angle qui appartiennent au monde intelligible; ce ne sont pas des objets sensibles qu’on peut par exemple toucher. Puis, ils raisonnent, par le biais de la représentation graphique, sur ces objets en dessinant des figures sur une feuille de papier ou sur un tableau. C’est en les dessinant que ces objets prennent vraiment naissance, si bien qu’on puisse les voir et même les toucher; car il n’y a pas d’objet mathématique en dehors du discours mathématique qui le définit et le caractérise. En d’autres termes, c’est la définition de l’objet qui donne naissance à l’objet lui-même. Il s’agit d’êtres abstraits qui n’existent que parce que les mathématicien·ne·s les désignent comme tels dans leur raisonnement. Par exemple, un cercle est un cercle à partir du moment où on le représente sur un support. Du point de vue des formalistes, les objets mathématiques font partie des systèmes essentiellement conventionnels, ceci dans la mesure où « les propositions mathématiques, comme leurs objets, sont vides de contenu. Les mathématiques se réduisent à un maniement correct des symboles. Ainsi donc les objets des mathématiques ne sont pas des objets en soi, et la pensée mathématique n’a d’existence que dans les codes symboliques qui la manifestent » (Owona, 2007 : 130). La définition mathématique est a priori alors que la définition des sciences d’observation est empirique. Aussi abstraite qu’elle soit, la définition mathématique est opératoire et la définition naturaliste est descriptive. Définir le carré comme un polygone ayant quatre côtés égaux et quatre angles droits, c’est créer et construire ce carré. Définir l’oiseau comme vertébré ovipare ayant des plumes et des ailes, c’est le découvrir à travers cette description.
En revanche, les mathématicien·ne·s raisonnent sur le carré en le traçant sur un support ou espace physique (le tableau, la feuille de papier, etc.). La mathématique est une initiation à l’abstraction; elle aide ainsi l’esprit humain à se détacher du sensible (c’est-à-dire du réel) vers l’intelligible (c’est-à-dire le rationnel). C’est elle qui prépare à toute dialectique philosophique. Mais Platon place la dialectique au-dessus de la mathématique qui, elle, reste encore imparfaite du fait qu’elle fonctionne encore sur la base d’hypothèses; les mathématiques sont une science hypothético-déductive. Pour lui, la dialectique est « la seule vraie science, puisqu’à travers les formes où il [sic] se déploie, elle remonte à la source de l’être. » [trad. de Baccou (1936 : XLV)]. Par exemple, un arbre existe puisque nous le voyons bouger sous l’effet de la force du vent. La seule idée d’arbre nous fait accepter immédiatement l’existence réelle de l’arbre[12].
Descartes et la pensée mathématique rigoureuse
La conception cartésienne met en avant la certitude des raisonnements mathématiques, leurs évidences, ainsi que la rigueur de leurs démarches qui partent toujours des problèmes simples et progressent vers les problèmes plus complexes; les démarches sont conçues selon un système méthodique qui ne saute pas les étapes. C’est ce qu’il exprime dans le propos suivant.
Je me plaisais surtout aux mathématiques, à cause de la certitude et de l’évidence[13] de leurs raisons : mais je ne remarquais point encore leur vrai usage; et, pensant qu’elles ne servaient qu’aux arts mécaniques, je m’étonnais de ce que leurs fondements étant si fermes et si solides, on n’avait rien bâti dessus de plus relevé. (Descartes, 2011 [1637] : 9).
Descartes pointe deux caractéristiques essentielles du raisonnement mathématique : la certitude et l’évidence. Le premier terme décrit une qualité fondamentale des résultats en mathématiques : toute solution avancée pour résoudre un problème mathématique est conçue en sorte qu’il n’y ait aucun doute sur sa validité. De même, ce résultat devra être compréhensible et visible sans l’intermédiaire d’une quelconque intervention extérieure.
Pour lui, les pensées isolées n’ont aucune valeur. Il est nécessaire d’enchaîner les idées de manière cohérente pour produire un savoir à l’abri de l’erreur. Il n’y a de raison qu’en un esprit qui conduit sa pensée par l’ordre et la rigueur. Dans son ouvrage Discours de la méthode, il explique à partir de son expérience personnelle ce que représente une démarche rigoureuse.
Règle 1
Le premier était de ne recevoir jamais aucune chose pour vraie, que je ne la connusse évidemment être telle; c’est-à-dire, d’éviter soigneusement la précipitation et la prévention; et de ne comprendre rien de plus en mes jugements, que ce qui se présenterait si clairement et si distinctement à mon esprit que je n’eusse aucune occasion de le mettre en doute. (Descartes, 2011 [1637] : 14)
Cette première règle porte sur la notion d’évidence. Le philosophe recommande de n’admettre pour vrai que ce qui ne souffre d’aucun doute. Il est donc important que les chercheur·se·s se débarrassent de toute idée fausse ou qui ne peut être prouvée.
Règle 2
Le second, de diviser chacune des difficultés que j’examinerais, en autant de parcelles qu’il se pourrait, et qu’il serait requis pour les mieux résoudre. (Descartes, 2011 [1637] : 14)
Le deuxième principe concerne l’analyse des phénomènes. Il est recommandé de toujours segmenter les phénomènes en de petites unités afin de les étudier en profondeur, en traitant toutes les étapes.
Règle 3
Le troisième, de conduire par ordre mes pensées, en commençant par les objets les plus simples et les plus aisés à connaître, pour monter peu à peu, comme par degrés, jusqu’à la connaissance des plus composés; et supposant même de l’ordre entre ceux qui ne se précèdent point naturellement les uns les autres. (Descartes, 2011 [1637] : 14-15)
La troisième règle se rapporte à l’ordre et à la cohérence des analyses : partir des objets simples vers les objets complexes.
Règle 4
Et le dernier, de faire partout des dénombrements si entiers, et des revues si générales, que je fusse assuré de ne rien omettre. (Descartes, 2011 [1637] : 15)
Cette dernière règle concerne des vérifications minutieuses pouvant ouvrir à des règles générales.
Il applique cette méthode de la manière suivante. Il commence par douter de tout, de nos sens, en disant que nos sens peuvent très souvent nous tromper. Par exemple, quand le soleil nous brûle, nous avons l’impression qu’il est juste au-dessus de notre tête alors qu’il est situé à une distance évaluée en centaine de millions de kilomètres de la terre. Il doute ensuite de tout ce qu’il a appris jusque-là, de toutes les démonstrations qu’on lui a proposées comme étant vraies. Il doute aussi de la réalité du monde extérieur; il se peut que les objets que nous voyons ne soient pas réels, de la même manière que les objets dont nous rêvons ne soient pas toujours dans la réalité. Il se peut que dans notre état d’éveil, nous soyons dans un rêve permanent, mais sans être conscients que nous sommes dans un rêve (Descartes, 2011 [1637]).
Le résultat auquel Descartes parvient au terme de son doute, c’est la certitude de sa pensée, sa conscience. Il peut continuer à douter de son corps, mais pas de son âme. Il se rend alors compte d’une première vérité : la réalité de son existence; le fait que lui, Descartes, existe; autrement, ce serait de l’absurdité, une pure folie. D’où l’assertion « Je pense donc je suis. » qui est en effet sa première vérité. C’est par celle-ci qu’il connaît et reconnaît son existence et c’est de cette vérité que vont découler toutes les autres. L’homme se caractérise donc par sa conscience et n’existe que dans la mesure où il est conscient de son existence pensante. L’essence de l’homme, c’est sa conscience.
De la même manière pour les mathématicien·ne·s, c’est après des hypothèses premières, des bases de raisonnement solides (axiomes, postulats, définitions, conventions, etc.) qu’il va construire toute une axiomatique, une suite de raisonnements. En effet, les postulats sont des propositions non (encore) démontrables que l’on décide d’accepter comme nécessairement vraies et dont il a besoin pour construire une démonstration. C’est ainsi que les mathématiques sont des constructions hypothético-déductives dont le caractère systématique et la cohérence interne reposent toujours et nécessairement sur un petit nombre de postulats. Ces outils créent l’univers dans lequel les mathématicien·ne·s veulent travailler. Par exemple, le 5e postulat d’Euclide stipule : « par un point pris en dehors d’une droite, on ne peut mener qu’une seule parallèle à cette droite. » À cette époque, ce n’était ni une évidence ni un théorème, car il n’était pas encore démontré. Dans la conception actuelle de la géométrie affine, cet axiome est devenu un théorème.
Les mathématiques sont pour l’esprit un moyen d’accès à la vérité par la démonstration, la rigueur et la cohérence. C’est pourquoi Descartes voudrait expliquer, de par la méditation philosophique, la méthode qui permet à la démarche mathématique d’enchaîner les énoncés clairs et évidents : « Ces longues chaines de raisons, toutes simples et faciles dont les géomètres ont coutume de se servir pour parvenir à leurs plus difficiles démonstrations » (Descartes, 2011 [1637] : 15) vont, aux yeux de Descartes, permettre à l’esprit philosophique de réaliser ses plus hautes fonctions dans la recherche de la vérité. La vérité cartésienne réside en ce qu’il voit évidemment, c’est-à-dire très distinctement et très clairement (Descartes, 2011 [1637] : 25). Il s’agit d’une évidence rationnelle, d’une certitude complète d’inspiration mathématique. En raisonnant maintenant chaînon par chaînon, il réhabilite tout ce qu’il a remis en doute. Pour lui, les mathématiques sont un modèle de pensée rigoureuse; elles occupent une place de choix en philosophie, et elles ont donné même naissance à toute une branche de philosophie des sciences, la philosophie des mathématiques (Whitehead & Russell, 1910).
Bachelard : les mathématiques comme construction de l’esprit
Pour Bachelard l’importance des mathématiques réside dans sa capacité inventive. Il semble avoir une attitude réservée à l’égard de l’axiomatique et du formalisme (Loi, 1984). La place des mathématiques dans les travaux du philosophe est tellement prépondérante qu’elles traversent toute son œuvre, comme le relève Martin[14] :
Il est impossible de lire Bachelard sans être saisi par l’importance attribuée à la connaissance mathématique. Importance est même trop peu dire : c’est d’omniprésence qu’il s’agit. Pour Bachelard, la mathématique est la pensée rationnelle par excellence et toute son œuvre démontre inlassablement que penser le réel, c’est le construire mathématiquement. (Martin, cité par Loi, 1984 : 1)
Les mathématiques intéressent Bachelard surtout dans leurs rapports avec la physique qui relève du réel.
La science physique a trouvé dans les mathématiques un langage qui se détache sans difficulté de sa base expérimentale et qui, pour ainsi dire, pense tout seul. Mais en fait, nous sommes obligés pour comprendre réellement une expérience physique de traduire sous forme d’expérience personnelle les conclusions que les mathématiques nous suggèrent. (Bachelard, cité par Loi 1984 : 2)
Les mathématiques constituent alors dans la conception bachelardienne des outils efficaces au service de la recherche en physique. Toutefois, il précise qu’il est nécessaire d’adjoindre au résultat mathématique l’expérience personnelle des physicien·ne·s. Il s’agit donc non pas de transposer les concepts mathématiques en physique, mais davantage de les adapter au développement de la science. C’est ce qu’il nomme « la rectification des concepts » (Loi, 1984 : 2). Le réel mathématique est une construction expérimentale, conçue en termes mathématiques. Ainsi, le modèle mathématique n’est pas rigide, mais se construit par une reformulation permanente des principes de base. Pour Bachelard, les mathématiques sont un langage indispensable pour les autres sciences avec lequel on peut bâtir ce qu’on veut selon le conventionnalisme mathématique, c’est-à-dire dans le respect strict de certaines règles bien connues et inhérentes à cette discipline. Elles produisent un double effet : au niveau du sujet (avec des potentialités intellectuelles, développement cognitif chez l’individu) et au niveau de l’objet (avec des applications dans la société). Il réconcilie ainsi la science et l’âme des savant·e·s. Cette réconciliation et ce syncrétisme entre les sciences et les humanités traversent pratiquement toute l’œuvre de Bachelard.
L’un des points de divergence entre l’approche bachelardienne et l’approche cartésienne de l’expérience scientifique concerne la démarche. Pour Bachelard, la méthode cartésienne est réductrice, parce qu’elle ne permet pas une extension par un renouvellement permanent de l’expérience pour l’éprouver, pour la « compliquer » (Bachelard, 2008 [1934]). Les théories scientifiques ne devraient donc pas être figées, car la pensée est un mouvement dynamique et le questionnement est permanent. Les connaissances du passé servent de base pour créer de nouvelles. On est donc dans un mouvement continuel, une succession qui ne craint pas les contradictions. C’est ce que pense Bachelard quand il affirme que : « Quand il se présente à la culture scientifique, l’esprit n’est jamais jeune. Il est même très vieux, car il a l’âge de ses préjugés. Accéder à la science, c’est, spirituellement rajeunir, c’est accepter une mutation brusque qui doit contredire un passé. » (Bachelard, 2015 [1934] : 17). Nous projetons chacun, sur le monde qui nous entoure, non seulement des sentiments, mais aussi toutes les dispositions héritées de notre passé culturel ou de nos traditions sociales. L’esprit sans être vide se donne toujours un univers; et puisque les mathématiques traitent du réel comme du possible, de ce qui est comme de ce qui peut être, pourquoi ne traiteraient-elles pas des choses de l’esprit? Les mathématiques réalisent la synthèse entre le sujet et le monde. Elles peuvent donner une représentation réelle à la pensée; la concrétiser à travers un modèle. Pour Soler, un modèle est « un cadre représentatif, idéalisé et ouvert, reconnu approximatif et schématique, mais jugé fécond par rapport à un but donné : prévoir, agir sur la nature, la connaître mieux, etc. » (Soler, cité par Sagaut, 2008-2009 : 38)
En mathématiques, il y a une cohérence entre l’image réelle et le modèle mathématique associé. C’est en libérant l’image de l’intuition, en la posant comme imaginaire au travers d’un modèle mathématique bien élaboré et non plus comme image du réel, que la mathématique dévoile sa véritable place. Pour Bachelard, l’imaginaireest au-dessus de la mathématique au même titre que la dialectique de Platon. En fait, les mathématiques ne chassent pas l’intuition, mais la structurent en l’élaguant de toutes imperfections. Si les mathématiques sont plus riches, c’est simplement parce qu’il n’y a jamais de contradictions internes dans le corps des mathématiques[15]. Il n’y a pas par exemple de contradiction entre la définition mathématique d’une onde, avec comme paramètres intrinsèques : l’amplitude, la fréquence et la longueur d’onde, et les équations d’échanges d’énergie dans l’effet photoélectrique. En mathématiques, c’est la raison qui crée, à travers leurs définitions, les objets et les outils qu’elle saisit et utilise pour démontrer.
Pour lui, on ne saurait remplacer l’image expérimentale par l’équation. En outre, le raisonnement mathématique va des prémisses aux conséquences. C’est en cela qu’est perceptible sa rigueur. On conclut sur la seule base de la chaîne démonstrative, sans rien admettre de l’extérieur. De ce point de vue et par analogie avec la phénoménologie des philosophes, la mathématique est une phénoménographie[16]. En permettant aussi de déchiffrer d’autres aspects de la réalité, elle devient ainsi, en plus d’être une science contemporaine, une phénoménotechnique (Ienna, 2019) capable de postuler le possible, l’inconnu ou l’infini (quand il faut conjecturer le comportement asymptotique de la dynamique d’un phénomène dont le modèle mathématique présente une forme itérative, on peut, dans certains cas, utiliser le raisonnement par récurrence). Ainsi, la science de la réalité cesse de se contenter du comment phénoménologique pour rechercher le pourquoi mathématique, la formation de l’esprit. Le raisonnement mathématique n’est donc pas simplement cohérent et rigoureux, il est aussi fécond et par conséquent efficace pour projeter, extrapoler; bref, pour prédire.
Le fait qu’en physique, il soit impossible de décrire un objet à travers l’espace (euclidien) et le concept de matière rend nécessaire de penser cet objet à travers un modèle mathématique qui renferme tous les paramètres caractéristiques intrinsèques de l’objet. En effet, si l’objet était parfaitement discernable (par la forme, la masse, la position, la vitesse, etc.), les mathématiques n’auraient qu’un rôle descriptif, donc resteraient extérieures au phénomène. Or, il n’y a que les mathématiques qui puissent fournir un modèle de compréhension et de caractérisation d’un objet indéterminé ou indéterminable, mais dont l’existence est établie dans un modèle. La mathématisation n’est donc pas seulement une description d’un réel étranger à l’entendement de l’homme, ou encore une recette (ou un décryptage) des lois mathématiques qui seraient inscrites à notre insu dans l’univers, mais elle est une construction. Pour Bachelard, les mathématiques sont techniques et tout à fait utiles au physicien, à l’architecte. L’expression « bâtir les mathématiques » trouve ici tout son sens pratique.
Kant et l’idée de l’« intuition sensible » en mathématiques
Même s’il n’a pas élaboré une philosophie des mathématiques à proprement parler, Kant a produit de nombreuses réflexions à la fois sur les concepts et les méthodes mathématiques. L’une des idées phares qu’il a développées sur la géométrie et l’arithmétique est celle de l’intuition, conçue comme des « images pures » de l’intuition de l’espace et du temps. Kant considère qu’une définition mathématique « est à la fois présentation d’un objet intuitif et d’un concept schématisé dans l’intuition » (Pierobon, 2003 : 93). L’activité mathématique se perçoit alors comme une pensée (intérieure) permettant le repérage d’un objet pensé et une schématisation de cet objet dans la pensée. De ce point de vue, Kant va considérer que la définition mathématique est réelle dans la mesure où elle met en relation un concept pensé et sa « réalité objective » parce que conforme au concept. Cela l’amène à conférer aux principes mathématiques une « certitude intuitive » (Pierobon, 2003 : 93).
L’autre idée qui rapproche la philosophie kantienne des mathématiques est sa conception du réel. En effet, le réel est donné chez Kant comme une intuition. Il suffit, pour s’en convaincre, de lire les définitions qu’il donne des notions telles que le temps et l’espace.
Le temps n’est rien d’objectif ni de réel, il n’est ni une substance, ni un accident, ni une relation, mais une condition subjective nécessaire en vertu de la nature de l’esprit humain […]. L’espace n’est pas quelque chose d’objectif et de réel, ni une substance, ni un accident, ni une relation, mais quelque chose de subjectif et d’idéal, issu de la nature de l’esprit par une loi fixe, à la manière d’un schéma destiné à coordonner absolument tout ce qui est apporté du dehors par les sens. (Kant, cité par Chenet 1994 : 166)
La perception subjective du réel chez Kant semble trouver un grand écho dans le mode de raisonnement des mathématicien·ne·s. Le réel en mathématique pure semble coïncider avec l’« intuition pure » chez Kant. Ce dernier considère que « la mathématique pure et notamment la géométrie pure, ne peut avoir de réalité objective qu’à la seule condition de concerner uniquement les objets des sens. » (2001 [1783] : 50). Pourtant, les objets mathématiques ne coïncident pas toujours avec les objets réels. Pour Kant, le principe de la coïncidence avec la réalité n’est pas valable en vertu du fait que « notre représentation sensible n’est aucunement une représentation des choses en elles-mêmes, mais seulement de la manière dont celles-ci nous apparaissent » (2001 [1783] : 50). Pour comprendre la conception kantienne des mathématiques, il faut d’abord partir de la distinction réalité objective / réalité subjective, puis relier à la seconde la notion d’intuition pure. En prenant le cas du géomètre, Kant situe sa démarche dans une réalité subjective en affirmant que tout se joue à travers son regard subjectif et sa pensée intuitive. Il se distingue ainsi du philosophe qui procède par analyse; lui procédant par construction, sans ressentir la nécessité d’avoir « les choses mêmes devant les yeux » (Kant, cité par Pierobon 2003 : 39).
Que l’on considère les conceptions de Platon, de Descartes, de Bachelard ou de Kant, les mathématiques sont aujourd’hui une discipline incontournable pour toutes les sociétés qui aspirent à une émergence dans les domaines technique, technologique, social, économique ou culturel (Perrin, 2003; Villani, 2010; Ziegler, 2012). Il est donc un préalable, aussi bien et surtout pour les enseignant·e·s que pour les apprenant·e·s, sans lequel, la compréhension, l’appropriation et l’enseignement des outils mathématiques à des fins utiles semblent périlleux : la connaissance profonde de l’organisation de cette discipline.
Analyse structurale de la discipline mathématique
De manière générale, les sciences mathématiques dans leur structure se caractérisent par un vocabulaire essentiellement mathématique, un ensemble dynamique d’objectifs et une démarche de raisonnement qui obéit à certains principes.
Un vocabulaire propre aux mathématiques
En nous appuyant sur les observations de Lavoisier en chimie et que nous pouvons étendre aux mathématiques, l’on peut distinguer pour toute science, des éléments de trois ordres qui semblent inséparables : « la série des faits qui constituent la science; les idées qui les rappellent; les mots qui les expriment. » (Lavoisier, 1789 : 170). En effet, l’un des aspects caractéristiques des discours mathématiques est sans doute la langue utilisée par les mathématicien·ne·s pour faire les mathématiques, la métalangue ou le métalangage mathématique, c’est-à-dire un système permettant de représenter la relation entre l’objet à décrire et son expression : « Les termes de ce système (symboles, catégories, opérations, etc.) sont aussi peu nombreux que possible, explicitement définis, généralisables et robustes. Ils permettent de rendre compte des phénomènes et d’effectuer des calculs dépassant la simple intuition mathématique. » (J. Chuquet, Gilbert & H. Chuquet, 2019)[17]. Ce vocabulaire comprend entre autres des objets, des outils, des symboles, des codes et des notions que nous pouvons ranger en trois différents types suivant la catégorisation proposée par Chevellard (1998) : savoirs prémathématiques, savoirs mathématiques et savoirs paramathématiques. Dans le premier cas, il s’agit d’apprentissage à la pratique mathématique pour les jeunes enfants (initiation mathématique, situations mathématisables, éveil mathématique, situations d’ordre mathématique, éducation mathématique)[18]. Dans le deuxième cas, ces savoirs renvoient aux opérations élémentaires telles que l’addition, la multiplication, la factorisation, la dérivation et autres objets géométriques (cercle, triangle, etc.) qui sont des programmes d’enseignement. Le dernier cas correspond aux processus de résolution des problèmes comme la démonstration, les paramètres, les équations, la modélisation, bref des notions-outils qui ne font pas toujours l’objet d’un enseignement systématique. En général, les objets de la connaissance mathématique restent abstraits. Certain·e·s auteur·e·s comme Davis, Hersh et Marchisotto les qualifient d’« objets mentaux » :
Dans le domaine des idées, des objets mentaux, ces idées dont les propriétés sont reproductibles sont appelées objets mathématiques, et l’étude des objets mentaux avec des propriétés reproductibles est appelée mathématiques[19]. (2003 : 441)
Ainsi, les mathématiques ont pour objet d’étude des « objets mentaux » ayant « des propriétés reproductibles », c’est-à-dire que l’on peut, sous les mêmes conditions ou hypothèses, multiplier les expériences pour aboutir à un résultat généralisable. Ce principe fondateur de la démarche en mathématiques est d’ailleurs proche du concept de « réfutabilité » ou « falsifiabilité » de Popper (2002 [1959]), appliqué aux sciences expérimentales. Autrement dit, quand on fait les mathématiques, on n’étudie ou ne manipule que des idées, des choses de l’esprit qui peuvent être maîtrisées comme si elles étaient des choses réelles, mises en évidence à travers des esquisses, des illustrations ou autres représentations.
La langue mathématique est ainsi faite d’êtres ou d’entités abstraites et de nature variée. On peut citer entre autres :
– les conventions d’abstraction, les désignations de formes géométriques;
– les constantes : 0, 1, +∞, i, e;
– les variables : x, y, z;
– les symboles : l’égalité (=), l’addition (+), la multiplication (x), l’appartenance (∈), l’universel (∀), l’existentiel (∃), le « et » logique (∧);
– les figures géométriques : le triangle, le carré, la ligne;
– les ensembles : les entiers naturels (![]() ), les entiers relatifs (
), les entiers relatifs (![]() ), les nombres rationnels (
), les nombres rationnels (![]() ), les nombres réels (
), les nombres réels (![]() ), les nombres complexes (
), les nombres complexes (![]() );
);
– les conventions (a^0=1)∧(a≠0), l’équation de Leonhard Euler[20] (eiπ + 1 = 0);
– la tautologie (∀x ∈ C ) [(1 +e-iπ) × x = 0] ∧ (i2 = -1).
Ces entités mathématiques semblent n’avoir aucune réalité objective en raison du fait qu’elles ne sont pas directement perceptibles dans la nature. Seulement, elles procèdent d’une opération d’abstraction par l’usage des symboles traduisant une intention de généralisation, car ces signes peuvent renvoyer à des signifiés et à des référents différents selon les contextes. Ces caractères universalisés, par le biais de l’abstraction, la convention et la généralisation, font ainsi des mathématiques une science ouverte au monde. Dans le même ordre d’idée, il faut souligner avec Guisti que dans leur subtilité « les mathématiques ne sont pas filles de la nature, mais de l’art. » (1999 : 26). En d’autres termes, les objets mathématiques ne sont pas des données naturelles et physiques perceptibles à l’immédiat, mais plutôt une construction, une élaboration méticuleuse et rigoureuse de l’esprit qui s’apparente à une œuvre artistique; ce qui permet d’appréhender le métier de mathématicien·ne à celui d’un artisan qui conçoit, affine et polit ses objets pour leur donner la forme la plus cohérente. D’Alembert n’expliquait-il pas déjà au XVIe siècle la poéticité du discours mathématique en ces termes?
L’imagination dans un géomètre qui crée n’agit pas moins que dans un poète qui invente. Il est vrai qu’ils opèrent différemment sur leur objet; le premier le dépouille et l’analyse, le second le compose et l’embellit. Il est encore vrai que cette manière différente d’opérer n’appartient qu’à différentes sortes d’esprits; et c’est pour cela que les talents du grand géomètre et du grand poète ne se trouveront peut-être jamais ensemble. Mais soient qu’ils s’excluent ou ne s’excluent l’un l’autre, ils ne sont nullement en droit de se mépriser réciproquement. De tous les grands hommes de l’antiquité, Archimède est peut-être celui qui mérite d’être placé à côté d’Homère. (2011 [1751] : 33)
La proximité entre poésie et mathématiques semble donc établie, même si les points de divergence se remarquent au niveau de la démarche : composition et esthétisation pour les poètes d’une part, abstraction et analyse pour les mathématicien·ne·s d’autre part. Il nous semble que la démarche mathématicienne tient à la nature même de leurs objets d’étude.
Les objets mathématiques proviennent, non de l’abstraction des objets réels, dont ils décriraient les traits caractéristiques, mais d’un processus d’objectalisation des procédés. Ils ne dérivent pas d’une réalité extérieure, indépendante [sic] de l’homme, dont ils représenteraient l’essence dépouillée des impuretés matérielles, mais ils formalisent l’action humaine (Guisti, 1999 : 25-26).
Si cette conception des entités mathématiques reflète la démarche habituelle des mathématicien·ne·s, trois points nous semblent poser des difficultés d’ordre épistémologique. D’abord, l’idée de la coupure d’avec « la réalité extérieure » qui serait « indépendante de l’homme » ne constitue qu’une posture parmi d’autres. Il existe bel et bien des approches mathématiques qui s’efforcent de ramener leurs objets d’étude aux objets réels. D’ailleurs, ces approches ont fait la preuve de leur efficacité dans des situations d’apprentissage à différents niveaux. L’idée n’est pas de dire que les mathématiques ne sont pas de l’abstraction, mais plutôt de dire que c’est aussi de la réalité. De même, le fait de concevoir l’activité mathématique comme détachée des humains laisse penser que les objets mathématiques, ainsi que leurs propriétés seraient des objets désincarnés; or, ce sont des constructions humaines, témoignage de l’intelligence des hommes et des femmes qui peuplent le monde. Enfin, Guisti affirme que ces objets constituent une représentation de l’« essence » des réalités que les mathématicien·ne·s dépouillent de ses « impuretés matérielles ». Cette vision correspond certainement à la logique classique, mais elle tombe en désuétude dès qu’on la rapproche des logiques modernes (théorie des ensembles flous, grammaire des catégories, théorie topologique de la déformation, etc.). Ces théories ne tentent pas de se débarrasser des « imperfections » du langage, mais elles les intègrent parmi leurs paramètres.
Pour Guisti (1999), le processus de génération ou la naissance de nouveaux objets mathématiques obéit à trois étapes essentielles, pour qu’on arrive à leur matérialisation.
Phase 1
Les objets mathématiques comme instruments de recherche : des méthodes démonstratives favorisant l’émergence de nouvelles théories et de nouvelles découvertes donnent lieu à ce type d’objets. Par exemple, la construction des ensembles usuels tels que l’ensemble des entiers relatifs (noté ![]() ), l’ensemble des nombres rationnels (
), l’ensemble des nombres rationnels (![]() ), l’ensemble des nombres réels (
), l’ensemble des nombres réels (![]() ), etc., dérive des travaux sur l’ensemble des entiers naturels (
), etc., dérive des travaux sur l’ensemble des entiers naturels (![]() ).
).
Phase 2
Les objets mathématiques comme solutions de problèmes : ces objets sont étudiés pour eux-mêmes sans rapports immédiats avec le contexte, mais dans le but d’une utilisation circonstancielle. C’est ainsi que le protocole de résolution des équations du second degré dans (![]() ), permet de résoudre des problèmes isomorphes dont la modélisation obéit à ce type d’équation.
), permet de résoudre des problèmes isomorphes dont la modélisation obéit à ce type d’équation.
Phase 3
Les objets mathématiques comme objets d’étude : il s’agit des procédés opératoires ou itinéraires techniques qui deviennent à leur tour des objets d’étude. En guise d’illustration, on peut citer les études portant sur la méthode du pivot de Gauss, par exemple.
Cette hétérogénéité des objets mathématiques soulève d’ailleurs la question de l’unité en mathématiques. Elle repose avant tout sur la nature des objets considérés. Les objets étudiés en mathématiques ne sont pas donnés dans l’expérience sensible. Il s’agit d’objets intelligibles et abstraits. En géométrie par exemple, le théorème de Pythagore ne porte pas seulement sur le triangle dessiné au tableau, mais sur une figure abstraite que l’on saisit par la pensée. De même qu’en arithmétique, ce ne sont pas des kilos de sel ou de riz que l’on additionne, mais des nombres abstraits qui renverraient à ces réalités. Selon Platon (Mansion, 1969), les objets mathématiques sont des êtres intelligibles séparés du sensible. Quant à Aristote (Van Riet, 1952), les objets mathématiques sont tirés des choses concrètes simplement par abstraction.
Donnons deux exemples concrets et simples pour illustrer la conception aristotélicienne.
Exemple 1 : L’énoncé du problème « Que donnent trois oranges augmentées de deux autres oranges? » peut être représenté naturellement de la manière suivante :
(a1)

Dans un premier temps, à l’aide des symboles + et =, cette représentation peut être traduite comme suit :
(b1)

De plus, si nous désignons une orange par le symbole ou la variable x, l’activité se traduit alors, mathématiquement parlant, par l’addition vectorielle suivante :
(c1)
(3, x) + (2, x) = (5, x)
Une autre modélisation plus simplifiée étant : 3x + 2x = 5x.
Il faut remarquer que les objets manipulés peuvent être substitués à d’autres (des enfants, des oiseaux, des pièces de pagne, des parfums, des cahiers, etc.) pourvu qu’ils soient de même nature et puissent par conséquent être confondus finalement. Et le résultat est donc de cinq oranges évidemment, et nous pouvons le vérifier en comptant simplement l’ensemble des fruits de même nature (oranges) obtenus à l’issue de l’augmentation. Nous constatons clairement que cette modélisation mathématique du phénomène réel en question (l’addition des oranges) épouse exactement la réalité.
Cette formulation littérale peut être traduite de façon formelle comme suit :
3x + 2x = (3 + 2) x = (5) x= 5x
On peut alors généraliser en considérant la suite d’instructions suivantes qui permet de réaliser pareille opération (addition) pour diverses quantités d’objets (fruits) de nature identique (orange).

Ainsi, l’activité « 520 cahiers augmentés de 731 autres cahiers donnent combien de cahiers au total? » devient difficile quand nous savons qu’il n’est pas aisé de comptabiliser autant de cahiers un à un. On se réfère alors au modèle mathématique généralisé précédent pour résoudre le problème. En effet, en désignant le cahier par la variable « x » par exemple, l’activité se traduit mathématiquement par :
520 x + 731 x = (520+731) x = (1251) x = 1251 x
Soit un total de 1251 cahiers.
Exemple 2 : La représentation naturelle de l’activité : « Que donnent trois oranges augmentées de deux bananes? » est la suivante :
(a2)

Dans un premier temps, à l’aide des symboles + et = , l’opération peut être traduite comme suit :
(b2)

De plus, en gardant x pour désigner l’orange, si nous désignons la banane par la variable y, qui est bien différente de x (sinon une banane serait égale à une orange – « une banane est une orange » est absurde), la traduction mathématique de cette deuxième activité peut s’opérer également par une somme vectorielle à travers l’équation bilan suivante :
(c2)
(3, x) + (2, y) = (5, x+y)
Et l’interprétation du résultat obtenu (le membre de droite de l’équation) signifierait simplement « 5 bananes-oranges », dont le détail est donné dans le membre de gauche de l’équation. Comme dans l’exemple précédent, le profane ou l’apprenant·e non averti serait alors tenté de traduire cette équation bilan par l’égalité suivante : 3x + 2y = 5(x+y). Mais attention ! Lorsqu’elle est traduite de la sorte, on aboutit à une absurdité.
En effet, on aurait 3x + 2y = 5(x+y)
= 5x + 5y.
Ce résultat est absurde, car l’équation aux dimensions[21], autrement dit, les quantités par nature de fruit ne sont pas respectées quand on passe d’un membre de l’équation à l’autre. En partant du membre gauche vers le membre droit de l’équation, les quantités augmentent; et dans le sens inverse, elles diminuent.
Il faut alors remarquer que le résultat n’est vraiment pas directement déterminable. Cette somme ne peut ni être égale à 5(x+y) ni 5x + 5y, ni 5x, ni 5y, car sinon x serait identique à y; ce qui est de toute évidence faux. Une seule réponse, qui reste purement d’ordre mathématique, est possible : (5, x+y), soit 5 bananes et oranges ou encore 5 fruits dont des bananes et des oranges. N’allez surtout pas écrire 5xy, car cette expression traduit une activité tout à fait différente de celle qui vient d’être énoncée.
Ces deux exemples nous permettent de montrer comment s’effectuent, s’organisent et se formulent les objets mathématiques. L’idée est avant tout de prouver que la relation des objets mathématiques au réel est possible et démontrable. Notre conviction est que cette conception qui s’efforce de réconcilier le concret et l’abstrait est certainement un moyen efficace de démystification, de familiarisation et d’émulation pour l’apprentissage et l’usage enrichissants des mathématiques à travers la manipulation de leurs outils.
Aussi, pouvons-nous distinguer, en nous inspirant de Chevellard (1998), trois niveaux de représentation en mathématiques[22]. Le premier est le niveau prémathématique. Il renvoie aux opérations mentales que tout être humain est en mesure d’effectuer dans sa sphère cognitive. Les exemples présentés en (a1) et (a2) en donnent deux cas pratiques avec l’association respectivement des objets de même nature (oranges) et de natures différentes (orange et banane), l’opération d’addition effectuée pour le premier cas (3 oranges et 2 oranges) et l’obtention d’un résultat (5 oranges). À cette étape, on ne recourt ni aux symboles mathématiques, ni aux symboles de formalisation. Il s’agit donc de l’intelligence naturelle des humains, leur habileté, leur capacité, leur faculté de réaliser des opérations de diverses sortes.
Le deuxième niveau est le niveau mathématique. C’est le début de la formalisation avec des opérations dotées d’une complexité réduite. Cette étape correspond aux cas (b1) et (b2) des exemples 1 et 2 plus haut. La formulation de l’opération d’addition telle que présentée ne pose pas une grande difficulté à l’esprit humain. Pourtant, on a l’intuition qu’on représente une opération abstraite.
Le troisième niveau est le niveau paramathématique. Celui-ci se rapporte aux opérations de formalisation de type complexe à travers des règles de réécriture, des procédures de résolution et des méthodes entre autres. Des exemples en sont donnés en (c1) et (c2), ainsi que la suite du développement.
Il nous semble que ce niveau est celui qui pose le plus de difficultés aux apprenant·e·s. La solution consisterait alors à amenuiser l’écart entre le niveau 1 et le niveau 3 de sorte qu’on ramène les expressions abstraites et l’énoncé formalisé à des objets concrets. En postulant que ce qui se fait au niveau 3 est d’une certaine manière à l’image de ce qui se fait au niveau 1 puis au niveau 2, on opte pour un dévoilement des « mystères » des mathématiques, pour une mathématique du réel vers le symbolique, du concret vers l’abstrait, du tangible vers l’immatériel. Précisons que même si les niveaux sont en corrélation, ils ne sont pas pour autant interdépendants. Cependant, notre choix d’un apprentissage et d’une utilisation des mathématiques pour le développement et l’épanouissement humain est en concordance avec un cinétisme, à la manière d’un mouvement de va-et-vient, entre les trois niveaux. Dans un tel contexte, le recours à l’expérimentation s’impose, car il faut bien que les apprenant·e·s se fassent une idée claire et surtout concrète de la notion qu’on souhaite leur enseigner. Il n’est pas question de proposer des mathématiques pour le contexte africain, mais d’inviter les enseignant·e·s de mathématiques en Afrique à plus d’expérimentation dans leur pédagogie.
Un ensemble dynamique d’objectifs
La recherche en mathématiques s’organise autour de deux grandes orientations : un ensemble d’études orientées vers des questions endogènes à la discipline (branche fondamentale) et un ensemble d’études orienté vers la résolution des problèmes humains (branche appliquée). Dans l’une comme dans l’autre tendance, un ensemble d’objectifs sont définis. Ceux-ci varient en fonction des circonstances, des contextes et des types de problèmes à résoudre. C’est en cela que les objectifs de la recherche en mathématiques sont conçus comme des objectifs dynamiques. En guise d’exemple, on peut citer les développements récents en probabilité avec la généralisation de certains théorèmes limites à des structures non vectorielles comme les groupes, la construction des modèles mathématiques plus élaborés pour étudier la dynamique spatio-temporelle de certaines maladies comme le paludisme.
Divers facteurs, tant sociaux que scientifiques, ont poussé les mathématiques à se développer en s’ouvrant davantage sur le monde humain et non humain. Cette ouverture se dévoile nettement et concrètement dans ses interactions avec les autres disciplines (Flato, 1990) : l’économie, la sociologie, la linguistique, la géographie, la biologie, la physique, la chimie, etc. L’attrait exercé par les mathématiques sur les tenants de ces disciplines se justifie principalement par la rigueur et la cohérence du raisonnement mathématique.
Une démarche de raisonnement démonstrative
La démarche adoptée par les mathématicien·ne·s est caractérisée par une logique de nature cartésienne : prudente, méthodique et systématique. Autrement dit, une démarche scientifique qui observe, mesure, interroge pour arriver à comprendre et à prouver. On en distingue différents types. La démarche inductive[23] (raisonnement inductif fini ou transfini) dont le raisonnement vise à produire des connaissances par des conclusions plus générales que les prémisses. Par exemple, le raisonnement par récurrence, avec ses trois étapes que sont l’initialisation, l’hérédité et la validation à l’infini[24]. La démarche déductive[25] regroupe le raisonnement par implication ou preuve directe, par l’absurde et par contraposée. La démarche hypothético-déductive (avec comme exemple le raisonnement par l’absurde) intègre les deux démarches précédentes. Ici, le raisonnement part des propositions ou des principes, notamment les définitions, les axiomes et les postulats à partir desquels les autres propositions sont déduites. Chercher à démontrer ces hypothèses revient simplement à remettre en question tout le système. La démarche récursive ou itérative vise à établir des connaissances déterministes qui sont reproductives dans le temps ou dans l’espace suivant une dynamique traduite par un modèle mathématique et la démarche par contre-exemple consiste à exhiber une connaissance particulière qui vient détruire une conjecture.
C’est inéluctablement pour leurs qualités propres que les démarches mathématiques sont reconnues : leur logique, leur rigueur, leur rationalité, leur esprit d’analyse et de synthèse, l’universalité de leurs résultats, leur caractère généralisable. Elles permettent par ailleurs de mieux structurer l’espace et le temps (Flato, 1990). La force de cette discipline réside donc dans les règles fondamentales qu’elle s’est données comme base de travail.
Principes du raisonnement mathématique
Le raisonnement peut être défini comme « une certaine activité de l’esprit, une opération discursive par laquelle on passe de certaines propositions posées comme prémisses à une proposition nouvelle, en vertu du lien logique qui l’attache aux premières. » (Blanché, 2019). La relation qu’entretiennent le raisonnement et la logique est de type essentiel d’autant plus que la logique se conçoit comme la « science relative aux processus de la pensée rationnelle[26] […] et à la formulation discursive des vérités. » (CNRTL, Logique, 2019). Issue du latin logica, elle est la « science des lois du raisonnement » (CNRTL, Logique, 2019); le substantif « raisonnement » appartenant à la même famille étymologique que « raison » et « rationnel » (Le Petit Robert, 2012). En général, on démontre ce qui n’est pas évident, ce qui est donné par l’abstraction, l’invention ou par l’intuition. L’intrication entre la logique et les mathématiques est telle qu’il nous semble impossible de séparer les deux disciplines. Aussi, pour accéder à la connaissance mathématique, il est impératif de posséder des notions fondamentales de la logique. L’objectif est donc de montrer qu’en apprenant et en s’appropriant les principes de la logique, on prépare mieux l’apprentissage et l’appropriation des mathématiques. Il convient de relever que l’influence positive de l’acquisition de quelques principes basiques de la logique, loin de se limiter à l’école, se déploie fort bien au-delà de celle-ci, notamment dans la vie courante. Pour Adda, cette acquisition favorise l’éclosion sagace.
Quel que soit le métier qu’exercera l’enfant, la gymnastique intellectuelle provoquée par l’étude de la logique sera plus utile à l’épanouissement du simple « bon sens » et de l’esprit critique nécessaires à tout citoyen que tout autre type d’exercice mathématique (résolution d’équations, constructions géométriques, etc.). (1971 : 3)
À l’école particulièrement, l’apport de la logique est fondamental. Sa compréhension à travers un minimum d’étude permet d’éviter les traditionnelles confusions entre « conditions nécessaires » et « conditions suffisantes » (Adda et Faivre, 1971).
Dans cette section, on répondra alors à trois principales questions : quels sont les principaux types de logiques mathématiques? Quels sont les principes du raisonnement mathématique? Quels sont les principaux types de raisonnement mathématique susceptibles d’être exploités dans le cadre de l’enseignement-apprentissage des mathématiques pour le développement humain?
Principaux types de logique
On distingue en général trois types de logiques mathématiques : la logique formelle, classique ou inductive, la logique matérielle, symbolique ou déductive et la logique dialectique.
La logique formelle, classique ou inductive
Elle se résume dans le schéma d’Aristote (Pellegrin, 2014) qui a analysé le syllogisme, établissant la nécessité d’une conclusion à partir de deux prémisses liées par un élément moyen qui n’apparait pas dans cette conclusion :
Tout homme est mortel; (majeure)
Or Socrate est un homme; (mineure)
Donc Socrate est mortel. (conclusion)
En situation de classe, l’enseignant·e·peut, pendant le cours de généralités sur les fonctions logarithmes et dans le but d’attirer l’attention des apprenant·e·s sur la singularité de l’ensemble de définition d’une fonction, de leur rappeler ce qui suit :
Toute fonction numérique a un ensemble de définition;
Or le logarithme népérien est une fonction numérique;
Donc le logarithme népérien a un ensemble de définition.
La logique matérielle, symbolique ou déductive
La logique symbolique ou logistique désigne le raisonnement qui utilise, comme les mathématiques, des symboles et non pas des mots. Elle tente de transformer les opérations logiques en autant de calculs. Ici, la vérité porte non plus sur la forme, mais sur le contenu des propositions[27]. Une illustration serait :
Toutes les disciplines enseignées (A) à l’école sont importantes (B);
Or les mathématiques (X) sont une discipline enseignée (A) à l’école;
Donc les mathématiques (X) sont importantes (B).
En passant au symbolisme, on obtient :
Tout A est B;
Or X est un A;
Donc X est B.
Ici en général, les relations entre les propositions sont celles d’égalité, d’inclusion, d’exclusion, d’implication, de conjonction, de disjonction, d’équivalence, etc. Ces relations sont bien présentes et couramment utilisées dans le vocabulaire mathématique.
La logique dialectique ou logique de questionnement
La logique dialectique signifie le mouvement de la pensée qui évolue par contradiction. Cette pensée va de la thèse à la synthèse en passant par l’antithèse. Les hégélien·ne·s et marxistes, partisans de la logique dialectique, rejettent le principe de non-contradiction, propre à la logique formelle. Ce dernier est au contraire le moteur d’une pensée féconde et du progrès scientifique. Hegel affirme d’ailleurs que « le mouvement dialectique [est] cette marche <Gang> s’engendrant elle-même, se conduisant elle-même plus en avant et revenant en elle-même. » (Hegel cité par Grandjean, 2009 : 37). L’objectif de la logique dialectique est d’adapter la pensée à la réalité. Elle est bien plus vivante dans un contexte coopératif et interrogatif.
Du point de vue classique, alors que la pensée logique est un outil intellectuel qui guide la recherche de la vérité et qui affranchit l’esprit des erreurs, la logique dialectique quant à elle se nourrit de la réalité. Elle est au service du progrès de la science. Pour nous, elle est une logique de questionnement. Les contradictions qu’elle soulève amènent la science à se développer, innover, progresser et se surpasser.
Principes mathématiques de la raison
La connaissance des quatre principes fondamentaux que sont : le principe d’identité, de non-contradiction, du tiers exclu et de la raison suffisante, issus de la logique formelle d’Aristote, est la condition nécessaire à l’exercice et la structuration de la pensée scientifique (Malanda Dem, 1977; Sagaut, 2008–2009). D’ailleurs, toute la science repose d’abord sur ces quatre principes avant d’éventuelles ouvertures à d’autres principes comme celui de la causalité, du déterminisme des lois, de la séparabilité des phénomènes et celui de la complétude, qui animent la recherche des modèles ou des lois dans presque tous les secteurs de la science macrophysique (Anta Diop, 2011 : 165).
Le principe d’identité
C’est le principe selon lequel une chose n’est égale ou identique qu’à elle-même. La logique classique le formule ainsi : X = X. La lettre ou variable X symbolise tout objet de pensée, proposition ou concept. Le principe d’identité n’est que l’expression codifiée du besoin de cohérence logique qui est l’exigence essentielle de la raison. Par exemple, lorsque le géomètre a défini l’hexagone comme une figure géométrique régulière ayant six côtés égaux, il va de soi qu’il garde toujours ce sens dans la suite de la démonstration. L’exigence d’identité s’oppose à toute équivoque et de ce fait elle renforce l’unicité.
Le principe de non-contradiction
Il n’est que la forme négative du principe de l’identité. Aristote l’énonçait ainsi : « il est impossible qu’une même chose soit et ne soit pas simultanément » (Aristote, cité par D’Aquin, 2012 : 224). Donc, si une chose n’est identique qu’à elle-même, elle ne peut pas être égale à une autre parce qu’il y aurait contradiction. La logique classique l’exprime ainsi : X est différent de non-X. Par exemple, une lampe ne peut pas être à la fois allumée et éteinte, et réciproquement.
Le principe du tiers exclu
Il pose une alternative : étant supposé que X et non-X sont contradictoires, un sujet est nécessairement soit X, soit non-X. Et il n’y a pas de troisième solution possible. Par exemple, un nombre réel non nul est nécessairement soit positif, soit négatif. Le principe du tiers exclu contraint à affirmer l’un et pas l’autre.
Le principe de la raison suffisante
Il postule que tout phénomène qui se passe dans la nature a sa raison d’être, c’est-à-dire les conditions qui expliquent cet évènement. La raison humaine est caractérisée par l’impérieuse exigence d’intelligibilité. Ce principe si fondamental en macrophysique par exemple est encore appelé principe de causalité. Il signifie que tout phénomène surgit d’une cause; autrement dit, tout fait a une cause et dans les mêmes conditions, la même cause est toujours suivie du même effet. Par contre, à l’échelle microphysique, le fait que l’interaction objet-instrument soit acausale, c’est-à-dire sans lien de cause à effet, vient nier ce principe. Toutefois, l’explication scientifique finale consiste toujours à découvrir, sous tout changement spatio-temporel, une loi ou une identité fondamentale.
Principaux types de raisonnements mathématiques
En général, on distingue entre autres la déduction, l’induction, l’analogie et le raisonnement hypothético-déductif. Toutefois, chez l’enfant de moins de 9 ans, il convient de noter que de nombreuses « erreurs de raisonnement » aux yeux de l’adulte ne sont en effet que la simple traduction des structures mentales[28] de l’enfant qui, pendant de longues années, diffèrent considérablement de celles des adultes.
Le raisonnement par déduction
La déduction est un type de raisonnement permettant d’aboutir à une conclusion partant d’une ou de plusieurs propositions dites prémisses (CNRTL, 2019). Autrement dit, la déduction est un raisonnement allant des principes à la conséquence entendue comme une conclusion déterminée par ces principes. Dans la conclusion analytique, la conséquence est implicitement contenue dans les principes. Le raisonnement est alors purement formel, car la conclusion n’ajoute rien aux prémisses. La forme la plus importante de la déduction analytique est le syllogisme. La réalité ici est que la conclusion dit toujours exactement la même vérité que les prémisses (Beall, 2019). On peut alors reconnaitre que la déduction est une démarche qui va du général (prémisses, axiomes) au cas particulier (conséquence, théorème).
Un autre exemple de syllogisme comme raisonnement déductif peut être formulé comme suit :
Tous les humains peuvent comprendre les mathématiques;
Or Je suis un humain;
Donc Je peux comprendre les mathématiques.
On remarque que la déduction est a priori indépendante de l’expérience.
Le raisonnement par induction
Le raisonnement par induction suit une démarche qui va du particulier au général, c’est-à-dire de l’observation des faits à la loi qui établit alors les rapports nécessaires et constants entre les phénomènes. Par exemple, ayant remarqué plusieurs fois que le corps se dilate sous l’action de la chaleur, on peut conclure que la chaleur dilate les corps. L’induction est dite amplifiante, car elle affirme une vérité au-delà de ce qui est vu. Elle n’est pas un raisonnement rigoureux comme la déduction. Le rapport qu’elle établit entre les faits observés peut être une simple coïncidence et non une loi universelle. L’induction est toujours a posteriori et essentiellement fondée sur l’expérience.
Le raisonnement par analogie
Le terme « analogie » vient du latin analogia, emprunté au grec (CNRTL, 2019), qui signifie « proportion, rapport, conformité ». Il s’agit d’une forme de raisonnement qui permet d’étendre notre connaissance. L’analogie est, de ce point de vue, plus féconde que la simple ressemblance visant à étendre la connaissance par la généralisation de tout ce qui est directement comparable. Elle sert à lier entre elles les choses appartenant à des domaines de connaissances assez différents. Par exemple, « le livre que je suis en train de lire me paraît bien agréable. J’achèterai sans doute un second livre de cet auteur ». Pour le démontrer par analogie, on raisonne ainsi qu’il suit : « le livre que je suis en train de lire me paraît bien agréable. J’estime que son auteur écrit bien. J’achèterai donc un second livre, car celui-ci m’a plu. » Je fonde ma décision sur la satisfaction que m’a procurée la lecture du premier livre. Le second livre, bien qu’a priori étant différent du premier, a quelque chose de commun avec celui-ci : ils ont le même auteur. Je suis bien conscient que les deux livres ne sont pas pareils (donc pas d’identité), mais je les rapproche tout de même du fait qu’ils sont écrits par le même auteur (donc il y a un rapport entre les deux objets).
Si ce raisonnement par analogie est vrai dans certains cas, il peut parfois conduire aux erreurs. Par conséquent, il n’est pas autant rigoureux pour analyser tous les types d’objets mathématiques que le raisonnement déductif. Toutefois, ce type de raisonnement a fait ses preuves dans de nombreuses autres disciplines : il a servi notamment à l’explicitation des constructions métaphoriques et figuratives qui représentent une proportion non négligeable de l’activité langagière chez les humains[29].
Le raisonnement hypothético-déductif
Le raisonnement hypothético-déductif est une méthode qui va de l’hypothèse à la conclusion, en faisant appel à des règles d’inférence et de déduction. Et puisque ce type de démonstration mathématique repose sur des hypothèses, on admet ces hypothèses; raison pour laquelle on parle également de système hypothético-déductif. Par exemple, si A = B et B = C alors A = C. Il faut noter que les certitudes mathématiques qui sont fondées sur les définitions, les axiomes et autres postulats reposent toujours sur ce qui n’est pas démontré, c’est-à-dire des conventions. Et chercher à démontrer ces hypothèses revient parfois à remettre en question tout le système.
Presque tous ces types de raisonnements reposent sur les principes de la logique mathématique. La logique formelle est un modèle de rigueur du fait des règles qu’elle se fixe. Toutefois, elle fige l’esprit dans la mesure où elle ne confronte pas ses propositions à l’expérience pour les vérifier. Ce type de logique peut ainsi entrer en contradiction avec un pan de l’esprit, voire limiter sa liberté de réflexion et d’exploration de l’expérience. Comme nous l’avons évoqué plus haut, toute une partie de l’activité cognitive humaine, en rapport avec l’imagination, la virtualité, reste inaccessible à la logique formelle. Sa rigidité s’oppose à la flexibilité, à la labilité et à la complexité des activités cognitives humaines : les humains ne raisonnent pas toujours, quelles que soient les circonstances, en ce qui concerne le vrai ou le faux.
Par contre, la logique dialectique s’applique mieux à l’expérience. Les hypothèses et les théories scientifiques sont évaluées et réévaluées, soumises à la contradiction et mises à l’épreuve des expérimentations. Elle est au service du progrès en science comme un arbitre, car les contradictions qu’elle soulève amènent la science à toujours innover et à s’inscrire sans cesse dans une dynamique de progrès. Au bout du compte, « Le facteur dialectique constitue donc l’âme motrice du progrès scientifique et c’est le principe par lequel seules pénètrent dans le contenu de la science, une liaison et une nécessité immanente[30]. » (Hegel, 1987 : 75). Les termes « liaison » et « immanente » renvoient à des notions clés qui vont déterminer certaines conceptions épistémologiques de l’évolution scientifique. La liaison nous renverrait alors à des conceptions de changements en science comme cela apparait chez Khun (1972) qui formule la révolution des idées scientifiques comme le résultat d’une dynamique discontinue; ou encore à la notion de rupture épistémologique chez Bachelard (2015 [1934]). Quant à l’immanence, elle a servi de principe de référence pour l’ensemble de disciplines dites structuralistes qui ont émergé au cours au milieu du XXe siècle.
Au-delà des qualités qu’on reconnait aux raisonnements logiques, une question d’ordre épistémologique s’impose à nous : peut-on faire de la démonstration mathématique la voie d’accès par excellence d’une vérité indiscutable? Diverses réponses, toutes aussi attaquables, ont été apportées à cette interrogation. L’une des plus emblématiques est sans doute celle de Hegel qui juge sévèrement la pertinence de la démarche mathématique d’autant plus que pour lui « C’EST UNE SCIENCE RATIONNELLE QUI NE PRODUIT QUE DES VÉRITÉS DE FAITS.[31] » (Philonenko, 2004 : 72). Le principal argument du philosophe concerne la nature extrinsèque de la relation entre l’opération mathématique (démonstration) et l’objet mathématique. La démonstration d’une proposition sur le triangle rectangle est extérieure à l’objet triangle lui-même; ce qui fait dire à Hegel que « le mouvement de la démonstration mathématique n’appartient pas au contenu de l’objet, mais est une opération extérieure[32] à la chose (raison) » (Hegel, cité par Philonenko, 2004 : 72).
Dans le cadre de la pratique quotidienne des mathématiques, la mobilisation d’un type de logique en adéquation avec un raisonnement mathématique est parfois très difficile pour l’apprenant·e suivant la qualité du discours mathématique tenu par l’enseignant·e. Cette situation survient très souvent quand l’énoncé de l’activité n’est pas clair, rendant ainsi difficile l’accès à la situation-problème; de même que des indications sur les outils nécessaires à mobiliser sont absentes. Dans la perspective de rendre moins complexes les relations entre la logique et le raisonnement mathématique, Durand-Guerrier recommande une approche pragmatique.
L’étude de l’articulation entre la logique et le raisonnement mathématique dans une perspective didactique mobilise de façon concomitante les analyses de types syntaxique, sémantique et pragmatique. Plus précisément, nous pensons avoir montré que l’analyse sémantique, qui renvoie à la fonction référentielle du langage, ouvre le champ des interprétations possibles d’un fragment de discours mathématique dans une situation donnée, ce qui nécessite, pour poursuivre l’analyse de revenir à la dimension pragmatique, en particulier en ce qui concerne les conditions d’énonciation et l’état des connaissances des sujets. […] l’importance des considérations de type pragmatique dans le discours des enseignants à l’intention des étudiants, dont par essence le contexte d’utilisation reste mal défini; ceci venant en quelque sorte pallier la quasi-absence de références explicites aux outils logiques susceptibles d’éclairer les pratiques mathématiques. (Durant-Guerrier, 2005 : 147)
Pour cette autrice, en plus des aspects syntaxique et sémantique à retenir dans les discours mathématiques destinés aux étudiant·e·s, il faudrait intégrer l’aspect pragmatique[33], à l’effet d’offrir à ces candidat·e·s aux pratiques mathématiques, et pourquoi pas à l’expertise mathématique, des indices de repérage d’outils logiques susceptibles de les aider à « démarrer ». Ainsi, l’énoncé de la consigne comportera des expressions telles que « démontrer à l’aide de…, en vous servant de…, en vous appuyant sur… ».
Aussi, l’articulation entre la logique et le raisonnement mathématique occupe une place de choix dans la mise en œuvre des démonstrations de qualité dans cette discipline. Les enseignant·e·s de mathématiques sont confronté·e·s à cette tâche au quotidien avec leurs élèves. En fait, cette tâche sera facilitée si les enseignant·e·s tendent une perche aux apprenant·e·s en leur fournissant une clé sur les deux nécessaires à résoudre le problème : les outils logiques fournis, il leur restera d’établir les liens avec le problème posé grâce au raisonnement déployé. Ce travail n’est ni une activité spontanée ni une découverte au hasard, mais une acquisition progressive. D’ailleurs, tout·e élève, au cours de ses études en mathématiques, est nécessairement appelé·e·à améliorer le niveau de son raisonnement jusqu’au seuil requis pour mieux s’en sortir dans cette discipline.
En plus de toutes les exigences relatives aux règles de raisonnement qui sous-tendent les bons discours mathématiques – clarté, précision, indication sur les outils à utiliser – la recherche fondamentale, comme la recherche appliquée dans cette discipline, offre des réponses utiles pouvant renseigner la jeunesse sur les enjeux et la dynamique des mathématiques.
Enjeux et dynamique de la recherche en mathématiques
Dire que les mathématiques présentent un enjeu pour les sociétés africaines, c’est les situer dans des contextes, c’est-à-dire des cadres spatio-temporels où elles seront à même d’améliorer positivement les conditions de vie des populations. L’un de ces cadres est inéluctablement l’école, lieu d’apprentissage, cadre institutionnel de formation. Comment parler de l’école quand on est enseignant, sans parler de soi, de son expérience personnelle. Je m’autoriserai donc ici l’emploi de la première personne pour être en harmonie avec moi-même, car c’est une histoire personnelle. Mon histoire est la suivante.
En 2008, je suis en situation de classe en terminale scientifique au lycée classique de Meiganga[34]. Pour introduire le chapitre sur les nombres complexes, je commence par un bref rappel sur les origines et la construction des ensembles tels que les entiers naturels, les entiers relatifs, les nombres rationnels et les nombres réels, en dévoilant les limites ou insuffisances de chacun de ces ensembles. Puis, à travers un exemple, je fais constater et établir l’impossibilité de résoudre certaines équations algébriques dans ces ensembles. Ce qui me conduit à annoncer aux élèves l’admission d’un nombre imaginaire i qui n’est pas réel et dont le carré est négatif (i2 = -1). Une situation mathématique jadis impossible avant ce niveau d’étude, où le carré d’un nombre ne peut être négatif. C’est alors qu’un jeune élève venant fraichement de la classe de première de la même filière, bouleversé par cette information, me demande : « Monsieur, à quoi servent finalement les mathématiques si des vérités d’hier sont chaque fois démenties? Hier, on ne pouvait pas diviser les entiers naturels ni les entiers relatifs, mais quelque temps après, on l’a fait pour les nombres réels. »
La question de ce jeune élève me laissa pensif, non pas parce qu’elle parait insensée, mais surtout parce qu’elle provoqua en moi une sorte de déclic qui va me conduire vers des questions hautement épistémologiques : que représentent les mathématiques pour cet apprenant? Que lui a-t-on dit et enseigné sur cette discipline jusqu’ici? Qu’est-ce qu’il n’a pas reçu et qu’il aurait dû recevoir pendant ses années d’apprentissage à la fois sur le but, l’utilité et les enjeux des mathématiques?
Des enjeux de la recherche et de l’enseignement des mathématiques
Dans la vie quotidienne, chaque personne croit à sa bonne étoile, à son destin et tente sa chance dans toute aventure qu’elle entreprend. En réalité, l’éducation scolaire ou universitaire ne laisse aucune place aux situations hasardeuses, car à l’école primaire, au lycée comme à l’université, on enseigne entre autres une culture de la raison, un esprit critique et de rigueur, un culte de l’effort qui ouvre à la compétitivité. Dans ces milieux, l’éducation vise des objectifs d’ordre moral, civique et rationnel. Les mathématiques comptent parmi ces disciplines qui portent ces valeurs, qui sont d’ailleurs inscrites dans les objectifs de son enseignement.
Objectifs de l’enseignement et de la recherche en mathématiques
À travers l’histoire, comme le montrent de nombreux travaux (Traoré & Barry, 2007; Michel, 2014), l’enseignement des mathématiques vise à :
- former un nombre toujours croissant de scientifiques indispensables au développement socioéconomique et culturel des nations[35];
- inculquer davantage aux humains du monde entier des connaissances mathématiques en établissant des relations justifiées entre les observations du réel, les représentations (schémas, figures, tableaux, systèmes, etc.) et les concepts nécessaires pour des études approfondies.
Parallèlement à ces objectifs de premier plan, il faut relever que l’enseignement des mathématiques vise secondairement aussi, comme l’attestent les travaux de Soriano (1998) :
- le développement des facultés cognitives de l’apprenant·e : rechercher, comprendre et apprécier les explications rationnelles aux évènements sociaux ainsi qu’aux phénomènes naturels et même métaphysiques;
- l’élargissement ou l’extension de son champ de réflexion et de raisonnement;
- la possibilité qu’il ou elle atteigne un niveau minimum d’instruction et une certaine maturité dans le discernement et le jugement;
- la possibilité d’une bonne organisation personnelle : savoir utiliser ses moments de loisir, cultiver et développer ses talents pour son plein épanouissement, profiter des possibilités offertes par le milieu et les structures sociales existantes pour adapter et appliquer ses connaissances et poursuivre soi-même son éducation en améliorant ses compétences professionnelles ainsi que ses conditions de vie;
- la facilité d’exercer valablement un métier, fut-il celui de mathématicien·ne ou non;
- la formation des citoyen·ne·s enraciné·e·s dans leur culture et ouvert·e·s au monde;
- le développement de la créativité, du sens de l’initiative;
- l’installation de la culture de l’amour, de l’effort, du travail bien fait et de la quête de l’excellence;
- l’adaptation aux réalités économiques ainsi qu’à l’environnement international, particulièrement en ce qui concerne la promotion des sciences et de la technologie.
En somme, les mathématiques visent à faire de l’humain à travers les âges, un être libre et doué d’un esprit critique, capable de remettre éventuellement en cause les stéréotypes, les archétypes et les structures existantes de sa société. Dès lors, elles intègrent commodément dans sa démarche le questionnement. Dans l’enseignement des mathématiques, la maîtrise du vocabulaire de base et du raisonnement logique doit permettre à tout individu de comprendre les théories les plus élaborées et des généralisations mesurées et destinées à développer en ce dernier l’esprit critique et l’aptitude (pratique ou opératoire) au raisonnement hypothético-déductif, tout en ouvrant divers univers de réflexion à ceux et celles qui voudraient réaliser des études approfondies en mathématiques ou dans les disciplines apparentées.
Les objectifs de l’enseignement des mathématiques, sans être dogmatiques, évoluent, comme le fait remarquer Ziegler :
Si l’enseignement des mathématiques à l’école est la réponse, quelle était la question? Quel est l’objectif principal de l’enseignement des mathématiques dans les écoles? J’affirmerai que : a) il n’y a pas qu’un seul objectif, mais au moins trois et (b) ces objectifs sont des cibles mobiles[36]. (Ziegler, 2012 : 8)
Les objectifs de l’éducation mathématique à l’école sont ainsi nombreux et surtout dynamiques, changeant en fonction des contextes et des époques. Ziegler (2012) les résume en trois principaux points : la présentation des mathématiques comme une partie de la culture humaine, la présentation de cette discipline comme un domaine dotant à chaque individu des capacités de trouver des solutions aux problèmes de la vie courante et enfin, son introduction comme un domaine d’étude. Ainsi, les objectifs de l’enseignement des mathématiques, au fil des années, sont façonnés et modulés selon les besoins et les circonstances. Et pour Ziegler, nous devons être attentifs en veillant à ce que les problèmes n’aient pas changé au moment où nous mettons en place les solutions (« les questions n’ayant pas fondamentalement changé au moment où nos réponses sont mises en œuvre »[37], 2012 : 8).
Mathématiques et résolution des problèmes sociétaux
La question du véritable rôle des mathématiques dans la vie humaine n’est pas récente, elle est même très ancienne (De Guzman, 1988). Mais à l’origine, elle n’était pas aussi pertinente qu’aujourd’hui, la société paraissant, de notre point de vue, plus intéressée par la philosophie, la théologie, la poésie, les fables, le théâtre, le sport, le cinéma. Avec le temps, des progrès scientifiques et technologiques considérables ont été réalisés, provoquant une véritable explosion des mathématiques, à tel point qu’on peut plutôt se demander aujourd’hui « où est-ce qu’on n’utilise pas les mathématiques? » (McElroy, 2004; Greenwald & Thomley, 2012). Dans la même logique, l’on pourrait avec Houpa Danga D. E. se demander plutôt « dans quels secteurs d’activités humaines n’utilise-t-on pas les mathématiques de nos jours? »[38]. Le rôle des mathématiques, tout en étant pluriel et multisectoriel, se divulgue au travers de ses deux principales branches.
Comme nous les avons décrites plus haut, les théories mathématiques fondamentales sont cette branche qui s’occupe essentiellement du développement en interne de cette discipline à travers des études et des recherches théoriques hautement abstraites sur des concepts, des notions et autres problèmes issus des mathématiques elles-mêmes. On parle alors d’intradisciplinarité des mathématiques. Godement (1963) fait observer que les notions d’ensemble et de fonction, auxquelles nous ajoutons la notion de relation, sont des notions essentielles sans lesquelles on ne peut rien faire d’intéressant en mathématiques d’une part, et avec lesquelles on peut tout faire d’autre part.
Dans cette branche, Hilbert (1900)[39] évoque de grands problèmes mobilisateurs autour desquels vient se greffer une multitude d’autres problèmes secondaires. Il s’agit là de la proposition d’une fondation formaliste pour les mathématiques qui, prise comme un but, établit la consistance et la complétude des systèmes mathématiques. Pour lui, si nous ne pouvons pas déclarer la vérité humaine absolue, essayons au moins de montrer la non-contradiction ou mieux la consistance absolue (Kindschi, 2005).
Ces théories fondamentales ont pour ambition de développer davantage les mathématiques, de peaufiner de nouveaux outils et d’approfondir les connaissances pures tout en saisissant les tournures au détail près. Elles jouent un rôle d’investigation, d’invention, d’abstraction, de construction et d’étude des propriétés quantitatives et qualitatives de nouveaux modèles mathématiques[40]. Elles représentent le socle des mathématiques et sont le domaine de grands chercheur·e·s et enseignant·e·s qui produisent des résultats et les diffusent à travers des publications dans des revues scientifiques avec parfois des objectifs d’apprentissage bien définis. Toutes les autres mathématiques puisent ici les énergies de leur développement. Pour les jeunes qui ambitionnent de faire carrière dans la recherche en sciences mathématiques, des sites et ressources documentaires utiles pour devenir un·e « bon·ne » mathématicien·ne existent (Tao, 2012).
Les théories mathématiques appliquées quant à elles sont cette branche qui est motivée par la volonté de comprendre mathématiquement des phénomènes liés à d’autres sciences; elles orientent leurs travaux vers la recherche de modèles et de domaines d’application de la pléthore de résultats des travaux de la recherche fondamentale. Elles recherchent des modèles concrets, des représentations ou des problèmes dans la vie courante pouvant bénéficier de tel ou tel résultat. Des notions comme les équations différentielles ordinaires ou aux dérivées partielles sont régulièrement utilisées en économie par exemple, comme nous le verrons dans le chapitre suivant. Les statistiques et les probabilités sont utiles en sciences politiques. Quand il faut mesurer la cote de popularité des politiques, candidat·e·s à un poste électif, on fait des sondages ou des enquêtes d’opinions. Ce type de travaux sont l’œuvre des ingénieur·e·s statisticien·ne·s, des chercheur·se·s ou enseignant·e·s relevant du domaine des mathématiques appliquées.
Sans toutefois méconnaitre la place toujours importante, mais souvent voilée de la recherche fondamentale aujourd’hui comme par le passé, il faut reconnaitre que les mathématicien·ne·s des sciences appliquées semblent en général mieux armé·e·s pour collaborer avec d’autres groupes de scientifiques, en particulier du fait d’une culture scientifique générale (les phénomènes étudiés relevant essentiellement du tangible) et du fait d’une habitude aux outils fondamentaux (mathématiques) de calcul et de l’espace. Certaines théories issues des mathématiques fondamentales qui ont connu d’innombrables applications restent difficiles à classifier comme appartenant exclusivement à l’une ou à l’autre branche. On peut citer par exemple la théorie des distributions de Laurent Schwartz, la théorie des EDP avec Pierre-Louis Lions et la théorie de l’homogénéisation de Gabriel Nguetseng[41].
S’agissant de la théorie de l’homogénéisation, le professeur Nguetseng par d’un constat : tout matériau est composite, mais souvent considéré comme un tout homogène. Ce qui n’est pas vrai. Il va donc développer une théorie qu’il va appeler « la théorie de l’homogénéisation » qui va répondre à cette inssuffisance. En effet, cette théorie va prendre en considération les hétérogénéités et construire un homogénéisé qui conserve les propriétés du matériau hétérogène considéré. Cette théorie trouve ses applications dans une variété de domaines : en mécanique (matériau composite), en médecine interne (cellule), en épidémiologie (modèles spatio-temporels) et en hydrodynamique (milieux visqueux hétérogènes), pour ne citer que ceux-là.
Le niveau d’intrication entre les deux principales branches des mathématiques est tellement élevé aujourd’hui que chacune d’elles, à sa manière, contribue à l’édification des différents enjeux de cette science dont nul ne doute plus de la transversalité. Les mathématiques sont une discipline transversale, un facteur d’unité et d’unanimité scientifiques.
Le rôle des mathématiques est également perceptible à travers le métier de mathématicien·ne
Être mathématicien·ne, c’est exercer une profession très utile pour les sciences et l’humanité, et même agréable pour les praticien·ne·s (Villani, 2010). En effet, le métier de mathématicien·e dans l’enseignement, dans l’industrie ou en entreprise a été placé en pole position du palmarès des 20 meilleurs métiers en 2009 dans la revue Wall Street Journal et en 2014[42], détrônant ainsi l’Actuariat qui l’était en 2013. Les critères de classement sont la qualité du cadre de travail, le niveau de stress, les perspectives d’emploi et le salaire. Dans ce classement 2014, les mathématicien·e·s viennent avant les professeur·e·s d’université et les statisticien·ne·s. Même si dans ce métier les salaires ne sont pas nécessairement mirobolants dans certains pays africains, si les carrières ne sont pas particulièrement exaltantes, les emplois restent à tous points de vue confortables. Nous constatons pour nous en réjouir que les métiers les mieux cotés par ce site en 2013 et 2014 soient aussi très étroitement liés aux mathématiques. Dans leurs « confortables emplois », les mathématicien·ne·s s’intéressent à la recherche et établissent des résultats d’ordre mathématique de bonne facture et il est possible d’en tirer des éléments de solution à des problèmes de l’humanité et son environnement, sur la base bien entendu des données ou des informations disponibles (Tao, 2012). Les résultats obtenus, après implémentation, sont validés par des comités scientifiques et rendus ou communiqués aux pouvoirs publics qui, seuls, peuvent décider de l’utilisation ou de l’exécution. Ainsi, pour une raison ou une autre et selon les intérêts qu’ils offrent aux instances décisionnaires, ces résultats peuvent être exploités totalement, partiellement ou simplement rangés dans les tiroirs, comme c’est parfois le cas.
Par ailleurs, en faisant une analogie avec les deux grandes branches enchevêtrées des mathématiques, Snow, reprise par Gowers dans The Two Cultures of Mathematics, classe les mathématicien·ne·s en deux grands groupes :
- les théoricien·ne·s (« theory-builders ») : il s’agit des créateurs et créatrices, des concepteurs et conceptrices de théories qui se préoccupent essentiellement de la construction et de la compréhension des théories; ces personnes s’intéressent également aux relations d’interdépendance qui pourraient exister entre les résultats mathématiques (souvent très abstraits) sommetoute individuellement significatifs. C’est dans ce groupe d’élite que se recrutent les génies dans le domaine.
- les inventeurs et inventrices de solutions (« problem-solvers ») : Il s’agit de ceux et celles qui se donnent pour objectif central de résoudre les problèmes courants liés à la compréhension d’une théorie; c’est-à-dire les exercices effectués dans le cadre des activités théoriques et des travaux pratiques d’apprentissage. C’est dans ce groupe que l’on retrouve entre autres les chercheurs et les chercheuses, les enseignants et les enseignantes, les ingénieurs et les ingénieures, etc.
Ici également, les deux groupes sont totalement interconnectés. Il n’existe pas de barrière étanche entre les theory-builders et les problem-solvers.
Mathématiques et enjeux pour le développement de l’Afrique
Les mathématiques présentent des enjeux certains pour l’Afrique aujourd’hui. Elles constituent, à coup sûr, l’une des clés du développement des communautés autant dans ses démarches singulières que dans les nombreuses interactions qu’elles construisent avec d’autres domaines du savoir; les mathématiques proposent des solutions viables pour sortir les communautés africaines de la pauvreté. Si une telle déclaration peut avoir l’allure d’une lapalissade, elle est avant tout une conviction et une posture qui a une force de réalisation. Mais les discours optimistes tout comme les réalisations pratiques sont nécessaires quand ils pèsent sur des consciences un certain nombre de préjugés défavorables. Aussi nous attèlerons-nous, avant de présenter des cas concrets d’émergence par le biais des mathématiques, de sensibiliser et d’éduquer en mettant en avant le gain, le profit, les avantages que l’Afrique tirerait d’une éducation mathématique orientée vers le développement.
Premièrement, les mathématiques sont au cœur de nombreuses activités humaines au point que l’on puisse dire qu’il n’y a pas de sociétés humaines sans mathématiques. Que l’on regarde un instant l’un des secteurs clés des sociétés tel que l’économie. Que l’on s’interroge sur le fonctionnement des systèmes économiques des pays du monde : de la production à la distribution en passant par le contrôle et la gestion des stocks. Dans tous les cas, on n’échappe pas aux opérations mathématiques. Aujourd’hui, l’un des secteurs les plus prometteurs dans les pays africains est sans doute celui de la technologie. Mais sommes-nous à même de dire que les Africain·e·s tirent le maximum de bénéfice des activités liées à ce secteur? Quelle proportion de cette population trouve-t-on parmi les producteurs et productrices de ces technologies? N’est-ce pas, dans la plupart des cas, des personnes réduites au simple rôle de consommateurs et consommatrices? Il convient alors de rappeler cette mise en garde d’Ouaro.
L’Afrique ne s’affranchira pas de sa dépendance à l’aide internationale tant qu’elle ne construira pas sa propre capacité à se développer. Pour ce faire et à l’instar des instituts africains des sciences mathématiques qui sont installés actuellement en Afrique du Sud, au Cameroun, au Rwanda, au Kenya et au Ghana, tous les pays africains devraient construire des centres nationaux d’étude et de recherche en mathématiques et développer des écoles d’excellence d’entrée dans les grandes écoles d’ingénieur. (Ouaro, 2018)
Deuxièmement, les mathématiques constituent un enjeu pour le développement durable des sociétés. Les phénomènes de changements climatiques ont pris une telle ampleur ces dernières années qu’il est impératif de mettre en place des dispositifs de surveillance et de protection du milieu naturel. Quelle discipline scientifique est-elle en mesure de fournir ces données sur la base des prédictions, de calculs des effets possibles et de projection afin de réduire l’avancée de ces types de problèmes? Pour nous, la réponse nous semble couler de source : les mathématiques.
L’érosion, la montée des océans, ou encore la gestion de la pêche sont, avec le changement climatique, des enjeux majeurs pour le développement économique d’un pays. L’étude et la compréhension de ces phénomènes nécessitant des outils mathématiques de plus en plus sophistiqués, il est capital de favoriser la formation à l’enseignement et à la recherche en mathématiques pour être en mesure de répondre à ces enjeux. (CNRS, 2019)
Troisièmement, l’apprentissage des mathématiques, comme ceux des autres domaines de connaissance, constitue une manière d’accroitre ses potentialités intellectuelles. Les mathématiques font ainsi partie de la culture humaine puisque l’activité mathématique constitue une pratique sociale. En tant que discipline à fort degré d’abstraction, les mathématiques concourent à rendre les humains meilleurs en leur donnant les possibilités de réfléchir, de se projeter et de se sortir des difficultés de divers ordres. D’ailleurs, pour Villani (2010), répondant aux questions de Jean-François Desessard sur les mathématiques en Afrique, l’étude des mathématiques est incontournable.
C’est un passage obligatoire pour que l’Afrique puisse prendre véritablement son envol au niveau scientifique […]. L’étudiant qui aura suivi un cursus de ce type, lui permettant d’acquérir des compétences cérébrales, pourra ensuite s’adapter quasiment à toutes les thématiques. À travers une assise théorique, il ne s’agit pas de se contenter de former des scientifiques, tâche bien sûr capitale, mais aussi de préparer ceux qui, dès demain, pourront se retrouver aux commandes du développement économique de leur pays. (Rivasseau et al., 2010 : 8)
En outre, les mathématiques participent aussi à la construction d’un imaginaire humain riche. Elles sont, d’une certaine façon, un travail artistique par leur aspect esthétique et architectural, leur vocabulaire énigmatique, leurs démarches inventives, leurs formules élégantes. Il existe de nombreux travaux qui établissent des rapprochements assez frappants entre, par exemple, le langage poétique et le langage mathématique (Marcus, 1968; Le Cor, 2014).
Par ailleurs, l’un des défis les plus importants à relever par l’Afrique est celui de la langue. Pour que les Africain·e·s s’approprient et exploitent efficacement les avantages qu’offrent les mathématiques, il est utile de relever le défi des mathématiques en langues africaines. Précisons tout de suite que nous n’opposons pas les langues africaines aux langues européennes héritées de la colonisation et qui sont encore, dans de nombreux pays africains, la langue de l’accès aux savoirs. Pour nous, ces langues se complètent et chacune joue une fonction importante au sein des sociétés. Il reste cependant que le développement et l’acquisition des connaissances dans des langues endogènes profiteraient à un public beaucoup plus large. Mais il y a un préalable : il faut inventer une terminologie pour transmettre les mathématiques en langues africaines. L’enjeu est tel que des linguistes à l’exemple de Diki-Kidiri (2008) se sont emparés de la question. Voici l’une des situations qui motivent leurs démarches.
Un chef de service africain, ayant bénéficié d’un stage de formation en bureautique à l’étranger, doit former à son tour toutes les secrétaires de l’institution où il travaille. Mais plusieurs de ces indispensables personnes maitrisent mal le français et pas du tout l’anglais. De plus, n’ayant jamais travaillé autrement qu’avec de vieilles machines à écrire mécaniques et des méthodes antédiluviennes, elles éprouvent une véritable angoisse devant la perspective de se mettre à l’ordinateur, avec tout le bouleversement que cela implique. La direction décide de tenter l’expérience d’une formation donnée dans la langue africaine commune à tous. La question est de savoir comment rendre dans la langue africaine en question tous les concepts inédits qui entrent en jeu dès l’utilisation d’un ordinateur. (Diki-Kidiri, Mbodj & Baboya Edema, 1997 : 95)
Pour combler ces manques, linguistes et terminologues travaillent depuis plusieurs années à la mise en place des vocabulaires scientifiques dans des domaines aussi divers que la santé (Tourneux & Métangmo-Tatou, 2010), l’agropastoralisme, les technologies (Diki-Kidiri, 2008) entre autres. Ces travaux auront aussi pour avantages de revaloriser les langues africaines qui renferment en leur sein des savoirs locaux qui méritent d’être enseignés (Tourneux, 2011). Les mathématiques, l’un de cet ensemble des savoirs fondamentaux, ne pourront que profiter avantageusement du développement d’une terminologie en langues africaines. C’est une pierre à l’édification, à la contextualisation de la discipline, un témoignage de son dynamisme.
La dynamique mathématique : une science ouverte au développement humain
S’il est vrai que toute science se développe aux frontières d’autres disciplines avant de s’intégrer dans une philosophie, la recherche mathématique est aujourd’hui tellement foisonnante qu’il serait bien présomptueux de :
- prétendre avoir cerné toute l’histoire de son évolution;
- donner un panorama des progrès réalisés récemment;
- dessiner les grandes tendances de son futur.
Pour nous, il ne s’agit pas de présenter de manière exhaustive la chronologie des mathématiques en exhibant les grands moments de l’histoire des mathématiques (Baumann, 2004-2005; Greenwald & Thomley, 2012 : 1091-1107) et de donner des réponses aux questions « qui?, quand?, quoi?, où?, comment? » concernant les principales étapes du développement de la pensée mathématique. Nous allons simplement nous contenter, ici, de décrire quelques domaines qui paraissent les plus révélateurs du foisonnement et du développement des mathématiques.
Mutations au cours de l’histoire
Historiquement, les mathématiques se sont développées en réponse aux nombreuses exigences humaines, et à la suite multiples influences d’ordre internes ou plutôt inhérentes à elles-mêmes. Au-delà de l’héritage inestimable constitué de nombreux travaux mathématiques et de recherches sur les mathématiques[43] de l’Europe ancienne, des Indo-Arabes du moyen âge et leur expansion et traduction en occident, il faut noter qu’au début du siècle dernier, le mathématicien Hilbert avait proposé, à l’occasion d’un congrès international de mathématique tenu à Paris en 1900, une liste de 23 problèmes mobilisateurs autour desquels viendraient se greffer tous les autres problèmes de mathématiques du XXe siècle, et dont certains restent encore non résolus de nos jours.
À côté de cette liste, il fallait également ajouter une tendance forte de cette époque : celle d’essayer de faire reposer les sciences mathématiques sur des bases solides. Des débats passionnés sur le statut des objets mathématiques, en réponse à l’espoir de pouvoir fonder des mathématiques de façon logiquement correcte et universelle, ont débouché sur l’ébauche d’un programme dit unificateur qui avait d’ailleurs connu à cette époque un succès éclatant. En effet, il avait permis de présenter les mathématiques d’une façon beaucoup plus formalisée qu’autrefois et avait été perçu par le grand public à travers ses mutations dans l’enseignement :les mathématiques modernes. Des personnes de bonne volonté de l’époque se sont alors dit; puisque ça marche si bien, pourquoi ne pas le mettre tout de suite dans les programmes scolaires! Ce qui fut aussitôt fait.
Par ailleurs, il y a eu chez les mathématicien·ne·s depuis une vingtaine d’années environ, une réorientation assez remarquable de leur philosophie de travail portée vers le retour au concret (McElroy, 2004; Stewart, 2006; James, 2003). Il s’agit en clair d’une intégration de plus en plus grande des mathématiques, au sens où il est très fréquent aujourd’hui qu’un concept né dans un domaine des mathématiques soit appliqué, et souvent avec beaucoup de succès dans une autre discipline parfois très insoupçonnée. Cela reste valable pour des concepts nés en dehors des mathématiques, surtout en physique, en informatique ou même en biologie.
Dans l’option de l’universalité, la science en général et les mathématiques en particulier devraient être omniprésentes, c’est-à-dire les mêmes pour tout le monde et partout dans la validation et la validité de ses résultats quel que soit le domaine de travail (Villani, 2010). Nous espérons que chaque cadre de contextualisation[44] aidera les apprenant·e·s et le reste de la population, à voir les mathématiques d’abord comme une discipline qui transcende la culture, le temps et le genre; et ensuite comme une discipline pour tout le monde (Greenwald & Thomley, 2012). Si l’on considère par exemple l’égalité 1 + 2 = 3 dans laquelle les nombres sont écrits avec des symboles de la culture euro-occidentale, elle doit être vraie aussi bien dans une école de savane du Kamerun septentrional que dans une école de banlieue parisienne, dans une école d’un quartier pauvre de New Delhi que dans un laboratoire scientifique des États-Unis. Seule la formulation ou la notation doit pouvoir différer d’une culture à une autre, soit I + II = III dans la culture romaine, (- + =) vaut (≡) dans la culture hindoue ou encore dans la culture arabe.
Le système de calcul babylonien était un système numérique sexagésimal (c’est-à-dire de base 60). En revanche, le système moderne, le nôtre, qui dérive de la combinaison entre les systèmes de numération indien et arabe, est décimal (c’est-à-dire de base 10) puisque nous comptons par groupe de 10.
Par ailleurs, la notation de la fraction avec une barre horizontale a/b est d’origine arabe, la notation avec deux points (a : b) vient de Leibniz (au XVIIe siècle) et la notation avec une barre oblique (a/b) date du XIVe siècle. Des notations ont souvent évolué avec le temps pour symboliser la même entité.
Comme nous l’avons évoqué antérieurement, les sciences mathématiques jouent déjà un rôle primordial dans le développement d’une éducation transversale comme outil de préparation à l’abstraction, comme aide à l’apprentissage du raisonnement et des sciences en général. La logique inhérente à la démarche mathématique est de plus en plus prisée dans les autres disciplines, en raison de ce qu’elle se prête facilement à une compétitivité intellectuelle qui, plus tard, débouche sur une compétitivité en toute dimension, dans n’importe quel domaine. Et pour mieux comprendre cette subtile logique mathématique, il convient de porter un regard sur la dynamique de la recherche dans certains domaines.
Évolutions remarquables dans certains domaines
Parmi les domaines scientifiques et des sujets considérés comme les plus dynamiques (CNRS, 1992; Greenwald & Thomley, 2012), nous pouvons retenir entre autres :
- la physique statique, la géométrie algébrique, les réseaux de neurones;
- les théories de la complexité (complexité de calcul et d’algorithmes, mathématiques discrètes);
- les travaux sur les rapports imprévus entre le chaos quantique et l’hypothèse de Riemann. La décomposition en ondelettes contribue à l’étude des phénomènes chaotiques, de la turbulence au sein d’un gaz;
- l’utilisation de la théorie de jauge issue de la physique des particules dans la topologie des variétés différentielles de dimension quatre qui semblent être plus proches des variétés complexes que des variétés réelles;
- l’application des algèbres d’opérateurs à la théorie des nœuds;
- l’utilisation des concepts de la théorie quantique des champs dans l’analyse sur les variétés et divers domaines géométriques et topologiques. Il s’agit d’une sorte de tentative d’unification des différentes forces qui régissent l’univers à l’exemple de la mécanique quantique et de la relativité.
En analyse par exemple, on est passé des fonctions numériques d’une variable réelle à celles de plusieurs variables réelles, et même aux variables complexes. Pendant cette extension, d’autres problèmes sont nés et ont demandé à chaque fois le développement de nouvelles recherches ainsi que l’utilisation des résultats mathématiques déjà existants. Une autre grande influence a été et demeure le besoin pour les mathématicien·ne·s de quantifier les autres disciplines. La majorité des problèmes et phénomènes du monde humain ou non humain, étant de nature dynamique[45], McElroy (2004) et Sarah (2011-2012) soutiennent que la notion de systèmes (discrets, linéaires, non linéaires, différentiels, etc.) contribue largement dans ce sens; et elle reste très exploitée dans la modélisation mathématique et la simulation.
La physique se rapproche davantage de la topologie. Ainsi, le phénomène de localisation des déformations en mécanique des solides a été modélisé dans un opérateur tangent comprenant une partie locale et des conditions aux limites[46] avant d’être simulé. La recherche sur les équations aux dérivées partielles, la modélisation et la simulation se renforcent : des travaux sur les fonctions harmoniques, sur les surfaces minimales, sur les équations stochastiques, entre autres, sont nombreux.L’une des illustrations les plus éloquentes de la dynamique interne aux mathématiques est sans doute celle qui se rapporte à la conjecture de Poincaré. Travaillant sur la sphère de dimension trois en topologie, Poincaré (1903) présume que : « toute variété compacte de dimension n = 3 (ou plus), sans bord et simplement connexe, est homéomorphe à une sphère de dimension n ». En termes plus simples, cette conjecture pourrait se traduire, grosso modo, par : « la sphère est le seul espace tridimensionnel fermé dépourvu de trous ». Cette affirmation qui concerne un problème majeur en topologie résista à toutes les tentatives de résolution jusqu’en 2003, lorsque Perelman en proposa une solution (Tummarello, 2006). Le second exemple beaucoup plus concret se rapporte aux travaux de Hales (2001 [1999]) sur l’utilisation de l’espace de façon optimale et avec un minimum de matériaux. Il a démontré mathématiquement le « théorème du nid d’abeille » précédemment connu sous le nom de « conjecture du nid d’abeille », en prouvant que contrairement aux divisions d’espace en carrés ou en triangles équilatéraux, la division en hexagones réguliers est la mieux appropriée pour partitionner un espace en parties égales avec une structure minimale. Ce résultat est aujourd’hui une ressource pour les architectes et ingénieurs en aéronautique, entre autres, qui s’en inspirent pour créer des structures qui, tout en étant solides, optimisent l’utilisation de l’espace.Dans divers domaines tels que l’informatique, la physique, la chimie, la biologie, l’histoire, les sciences ont établi au fil du temps des vérités durables; faisant ainsi l’unanimité chez tous les esprits éclairés et compétents en chacun de ces domaines. Jaspers l’avoue d’ailleurs quand il déclare que « les sciences [au rang desquelles les mathématiques] ont conquis des connaissances certaines, qui s’imposent à tous. » (1981 [1950] : 5)
Des évènements scientifiques à travers le monde
Sur un autre plan, l’Union mathématique internationale (UMI), avec le soutien de l’UNESCO, a fait de l’année 2000 l’année mondiale des mathématiques (UNESCO, 2019)[47]. Dans le prolongement des acquis de cette année mondiale, l’UNESCO proclame le 14 mars de chaque année comme la journée internationale des mathématiques. Celle-ci aura pour objectifs de faire mieux connaitre « la place des mathématiques dans le domaine des sciences, des technologies et de l’innovation, ainsi que le rôle de leurs applications dans la promotion de l’éducation, l’amélioration de la qualité de vie dans le monde et la réalisation des Objectifs de développement durable. » (UNESCO, 2019 : 2).
L’UMI a placé l’année 2000 sous le signe de la culture et de la paix[48] dans le monde, y compris dans les milieux scolaires. À cette occasion, une large réflexion a été menée sur le rôle des mathématiques comme un véritable facteur de développement. Les grands défis mathématiques du XXIe siècle ont été énoncés, en particulier la diffusion plus acérée des mathématiques au sein du grand public, la valorisation plus concrète de leur interdisciplinarité. En outre, la question de l’importance de l’image des mathématiques au sein l’opinion publique a été abordée. Autrement dit, il est question non seulement de faire découvrir au grand public la vitalité des sciences mathématiques, mais aussi d’engager également les mathématicien·ne·s à sortir de leur tour d’ivoire pour expliquer ce qui se fait et l’enjeu de ces actions pour l’humanité.
Faire sortir les mathématiques de leur invisibilité, c’est refuser d’entretenir leur image comme arme secrète des riches et des puissants. Les faire concourir au contraire au développement de tous les peuples, comme il est possible malgré les entraves, c’est bien les inscrire dans la culture de la paix mondiale à venir. (Tronel, 2000 : 22)
Au cours de la même année, un autre évènement majeur se déroule à Yaoundé au mois de septembre de l’année 2000. Les professeurs Bitjong Ndombol (Université de Dschang), Békollé et Louka (Université de Yaoundé I) ont organisé avec le soutien de Hogbè Nlend, alors ministre camerounais de l’Enseignement supérieur, un symposium sur deux thèmes : « Statistiques pour l’agronomie » et « Mathématiques et malaria ». Répondant à la question « pourquoi l’Afrique a besoin de mathématicien·ne·s? », Bitjong Ndombol fait l’observation suivante :
Le degré de développement d’un pays se mesure en très grande partie à sa maîtrise des sciences fondamentales et des technologies, et ce critère est tellement implacable que la présence d’énormes richesses dans son sous-sol ne modifie pas considérablement le classement d’un pays (prédominance de l’or gris sur l’or noir, l’or vert, l’or jaune…). (Bitjong Ndombol, cité par Dutertre & Békollè, 2001 : 40)
En 2007, un atelier scientifique sur le thème « Les changements climatiques : des modèles globaux aux actions locales » avait été organisé par l’Institut de recherche des sciences mathématiques à Berkeley aux États-Unis. Au cours de cet atelier, plusieurs sujets de recherche en mathématiques, pouvant contribuer à la résolution des problèmes dont les solutions auraient un grand impact sociétal, avaient été identifiés (Ziegler, 2012).
En 2012, la 4e Conférence européenne des étudiants en mathématiques (EuroMath 2012) a eu lieu à Sofia en Bulgarie, du 21 au 25 mars. Cet évènement annuel était organisé par la Société mathématique de Chypre et la fondation Thales. EuroMath met en place un forum pour les étudiant·e·s âgé·e·s de 12 à 18 ans afin qu’ils présentent, échangent et développent leurs idées, leurs créations en mathématiques dans un contexte international (Makrides, 2012).
Au cours de la même année, s’est tenu du 03 au 07 décembre, le 2e atelier scientifique Cryptographie, algèbre et géométrie (CRAG) 2 à l’Université de Ngaoundéré, avec plus de 48 participant·e·s venu·e·s du Tchad et de six universités camerounaises. Ces ateliers qui se tiennent tous les deux ans servent de cadre d’échanges entre aux chercheur·e·s qui travaillent sur les aspects théoriques, informatiques et appliqués de l’algèbre, de la géométrie et de leurs applications en cryptographie. Grâce à ces rencontres, l’utilisation des plateformes de calcul (SAGE, GAP, etc.) connait un essor remarquable au sein de cette communauté de spécialistes. Cela a pu permettre d’explorer de nouvelles structures mathématiques, de vérifier des conjectures, de suggérer des généralisations, tout en trouvant de nouvelles applications et en posant de nouveaux problèmes.
L’initiative Mathematics of Planet Earth (« Les mathématiques pour la planète Terre ») lancée en 2013 met au cœur des préoccupations les enjeux des changements climatiques et la réponse mathématique au problème. Ainsi, des recherches sont menées dans le cadre des doctorats afin de comprendre, de prédire et de dévaluer le risque pour l’humanité dans le cadre de la lutte contre les changements climatiques. Les étudiant·e·s sont formé·e·s aux techniques mathématiques et outils informatiques utiles pour résoudre ces questions :
Un étudiant en MPT (Mathématiques de la planète Terre) du CFD (Centre de formation doctorale) recevra une formation doctorale par cohortes sur les techniques mathématiques et informatiques nécessaires pour comprendre, prévoir et quantifier les risques et les incertitudes liés aux conditions météorologiques extrêmes et au changement climatique.[49] (Mathematic of Planet Earth, 2020, paragr. 3)
L’éducation mathématique étant une quête permanente des attitudes et des valeurs positives, la feuille de route pour la mission dévolue à cet effort mondial recommandait une fois encore :
- l’augmentation de l’engagement des mathématicien·ne·s de même que le grand public sur le rôle des mathématiques relativement aux sujets qui affectent notre planète et son futur;
- l’encouragement des chercheur·e·s à identifier et à poser des questions fondamentales relatives à notre planète et auxquelles les mathématiques pourraient contribuer à trouver des solutions appropriées;
- l’encouragement des enseignant·e·de mathématiques de tous les niveaux à traiter des sujets en rapport avec notre planète, à travers le développement de leur approche et des programmes scolaires contextualisés;
- l’encouragement des apprenant·e·s de mathématiques et chercheur·e·s débutant·e·s à poursuivre la recherche sur des sujets en rapport avec notre planète;
- la sensibilisation du grand public sur les rôles des mathématiques dans la résolution des problèmes de la planète Terre.
Par ailleurs, en Afrique comme dans les autres parties du monde, diverses plateformes de recherche, de formation, de renforcement des capacités et d’échanges en mathématiques ont vu le jour à travers la création des sociétés savantes et des programmes d’éducation/formation : l’Union mathématique internationale (UMI), l’American Mathematical Society (AMS), l’European Mathematical Society (EMS), la Société mathématique de France (SMF), la London Mathematical Society (LMS), l’Union mathématique africaine (UMA)[50], l’Université virtuelle africaine (UVA) et tout récemment l’African Institute for Mathematical Sciences (AIMS) avec des représentations encore appelées centre d’excellence dans plusieurs pays africains. Chaque centre d’excellence de cet institut travaille en partenariat avec la Fondation Mastercard et le gouvernement du pays d’accueil à travers son ministère compétent. AIMS vise d’une part en priorité l’amélioration des pratiques d’enseignement, d’apprentissage et d’expérimentation des mathématiques en situation de classe au secondaire, et d’autre part, l’accès et les opportunités de la formation universitaire en science, technologie, ingénierie et mathématiques (STIM), en particulier pour les filles. Dans la même logique, l’UVA est un réseau d’institutions africaines qui, en partenariat avec plusieurs universités africaines acquises à leur projet, propose de nouvelles offres de formations et de nouvelles méthodes éducatives basées sur les technologies de l’information et de la communication pour l’enseignement (TICE = TIC + Enseignement). Ainsi, l’UVA et l’AIMS œuvrent essentiellement dans la promotion de la science en général et des mathématiques en particulier à travers des programmes de recrutement, d’éducation et de formation en alternance des étudiant·e·s et des enseignant·e·s de mathématiques des lycées et collèges pour l’Afrique (Sokhna, 2006; Sokhna & Sarr, 2009; Karsenti et al., 2012). Toutefois, l’UMA et ces deux structures devront malgré leur jeunesse et l’avancée de la recherche dans le domaine des mathématiques, mobiliser davantage les ressources humaines, matérielles et financières nécessaires à leur développement afin de se faire aussi une place visible parmi les sociétés savantes.
Dans cette mouvance de développement de la recherche mathématique dans diverses régions du monde, l’Afrique n’est pas restée en marge. À travers l’histoire, une grande contribution d’ordre épistémologique des mathématiques africaines s’est faite à travers l’ethnomathématique[51]. Le terme « ethnomathématique » est utilisé pour exprimer les relations entre culture et mathématique :
Nous appellerons ethnomathématiques, les mathématiques qui sont pratiquées au sein de groupes culturels identifiables; des groupes tels que les sociétés tribales nationales, les groupes de travail, les enfants d’une certaine tranche d’âge, les classes professionnelles, etc.[52] (D’Ambrosio, 1985 : 45)
Le patrimoine mathématique riche de l’Afrique et l’apport pluriséculaire des Africain·e·s au développement des mathématiques sont incontestables au sein de la communauté scientifique (Traoré & Barry, 2007).
Aujourd’hui encore, certains pays d’Asie et de l’Extrême-Orient deviennent résolument émergents grâce à la science en général et particulièrement aux mathématiques et à la technique. Ces deux domaines se sont facilement déployés dans ces pays pour diverses raisons au rang desquelles l’existence d’un environnement psychosocial aménagé, approprié et propice à cet effet. Cet environnement se caractérise par l’existence et la promotion d’un profil mental de défi et de dépassement de soi, de discernement, de recherche du développement et de l’innovation; bref, d’une mentalité et d’un esprit scientifique.
Aujourd’hui, les mathématiques ont largement dépassé la conception selon laquelle seuls les faits logique et formel sont d’ordre mathématique. Elles sont inscrites dans la nature même. Et pour s’en convaincre, il suffit d’observer le fonctionnement de l’univers, comme l’avait écrit Galilée.
La philosophie est écrite dans cet immense livre qui se tient toujours devant nos yeux, je veux dire l’Univers, mais on ne peut le comprendre si l’on ne s’applique d’abord à en comprendre la langue et à connaitre les caractères avec lesquels il est écrit. Il est écrit dans la langue mathématique et ses caractères sont des triangles, des cercles et autres figures géométriques, sans le moyen desquels il est humainement impossible d’en comprendre un mot. Sans eux, c’est une errance vaine dans un labyrinthe obscur. (Galilée, cité par Chauviré, 1980 : 141).
Pour le savant italien, la nature est un immense livre qui renferme en son sein tous les savoirs (ici, la philosophie). Ces savoirs ne peuvent être compris qu’à condition que l’on sache lire ou déchiffrer les symboles de la nature qui sont analogues aux symboles mathématiques. On voit apparaitre ici, l’idée d’un discours mathématique crypté, et en même temps la nécessité d’une appropriation de la métalangue (« on ne peut le comprendre si l’on ne s’applique d’abord à en comprendre la langue et à connaitre les caractères avec lesquels il est écrit. ») fait de termes et de symboles spécifiques (« des triangles, des cercles et autres figures géométriques. »). Ainsi, la connaissance de l’univers suppose au préalable un effort de déchiffrement de la langue à travers laquelle il est exprimé. Cet effort, qui aboutit à la mise en place des concepts opératoires, des théorèmes et des théories, obéissant à des règles des plus rigoureuses possibles, va devenir au fil des siècles un modèle sur lequel vont s’appuyer de nombreuses disciplines scientifiques pour se développer.
Quelques tendances innovatrices
De nombreux problèmes de mathématiques trouvent leur importance dans l’intérêt qu’ils suscitent pour leur résolution et dans le développement des théories profondes qu’ils entraînent. Les questions sur les tendances et perspectives à venir en sciences, et singulièrement en mathématiques, ne sont pas nouvelles, elles restent d’actualité (Baumann, 2004-2005). Au regard des priorités contextuelles (Vergnaud, 1982), il est important aujourd’hui de discuter de ces questions afin de distinguer parmi les problèmes, ceux qui peuvent mener à des résultats probants et plus utiles dans l’avenir. Nous présenterons à la fois quelques questions abordées dans la recherche fondamentale en mathématiques et quelques autres relevant de la recherche appliquée.
On peut distinguer quelques grandes tendances avec un certain nombre d’implications. Il est certain que les problèmes changent et ne sauraient être posés de la même manière; des problèmes nouveaux naissent et concernent la nature et la méthodologie de l’enseignement des mathématiques et surtout la nature de ce que l’on cherche au bout du compte, c’est-à-dire les solutions, qu’elles soient exactes ou non.
S’agissant des théories fondamentales, relevons que l’histoire des mathématiques tient une place non négligeable à adjoindre à la didactique de cette discipline d’autant qu’elle est nécessaire à la formation des enseignant·e·s. Une présentation sommaire (et si possible sous forme d’un exposé) de l’histoire des mathématiques fondée sur la construction de grands concepts et théories mathématiques peut se révéler utile à leur assimilation (De Guzman, 1988; Baumann, 2004-2005). Cette tendance à l’histoire s’accompagne de plusieurs désirs : le désir d’enrichir le vocabulaire des apprenant·e·s avec les formes d’expression; de mieux contextualiser l’activité de recherche afin de bénéficier au maximum du développement de l’imaginaire humain à travers des interrogations adaptées aux contextes, captivantes et sources d’arguments; de mieux transposer le savoir enseigné et les méthodes d’enseignement du savoir; de mieux faire approprier les concepts (faire connaître les « crises » ayant provoqué le développement ou l’amélioration des concepts); et de mieux respecter la genèse des connaissances (avoir un regard sur la façon de concevoir et de relativiser les erreurs). La connaissance de la genèse des différentes notions, du type de problèmes ou de difficultés qu’elles contribueraient à résoudre et des obstacles qui ont surgi pendant leur construction, peut permettre à tout·e apprenant·e de mieux cerner ces notions (Vergnaud, 1982).
Cependant, il convient de rappeler avec Poincaré qu’« en mathématiques, la rigueur n’est pas un tout, mais sans elle il n’y a rien; une démonstration qui n’est pas rigoureuse, c’est le néant » (1908 : 27). Pour lui, c’est désormais l’économie de la pensée que l’on devrait viser. Il s’agit par exemple de répéter un raisonnement, un modèle ou un algorithme déjà fait en quelques lignes, sans pour autant rien sacrifier de la rigueur qui le sous-tend; même si certain·e·s mathématicien·ne·s continuent à développer une métalangue beaucoup plus abstraite et formalisée avec une volonté pratique profonde.
Depuis plusieurs décennies, une interaction tout à fait surprenante dans certains domaines est en train de s’établir entre les mathématiques et les autres disciplines scientifiques. En physique théorique par exemple, l’avènement de la mécanique quantique constitue, de ce point de vue, un fait important : une particule est une représentation de la notion de groupe; la gravité en théorie de la relativité est une propriété géométrique de l’espace-temps. Certains résultats mathématiques se démontrent par le biais de la physique, notamment en géométrie et en topologie. Le mathématicien-physicien Witten[53] a réussi, il y a une vingtaine d’années, à trouver, sans démonstration exclusivement mathématique, mais simplement à partir d’une intuition physique, des propriétés topologiques tout à fait remarquables dans la théorie quantique des champs. En achevant la démonstration du grand théorème de Fermat en 1994, le mathématicien anglais Andrew Wiles a mis fin à plus de 350 ans de recherche et ouvert ainsi la voie à la démonstration de nombreux autres problèmes mathématiques restés non résolus (Darche, 1993).
De nouvelles théories mathématiques sont nées et connaissent déjà d’importants succès. On peut citer : la théorie de la décidabilité en algèbre universelle, celle de la complexité de calcul qui traite des mathématiques effectives et dans lesquelles les objets qu’on manipule doivent être construits par des algorithmes (suites finies d’instructions). Les mathématiques discrètes, quant à elles, sont nées et se développent pour ces finalités. Ici, on s’intéresse non plus à des propriétés mathématiques en général, mais à des propriétés qui s’écrivent avec un nombre fini de symboles en un temps fini. Elles sont beaucoup plus liées aux machines telles que les ordinateurs, capables de traiter une masse d’informations.
Sur le plan des théories appliquées, les secteurs des technologies et des industries bénéficient largement des résultats de la recherche mathématique. Dans l’industrie par exemple, tous les problèmes de contrôle optimal sur la gestion et la stabilisation d’une structure, de calcul scientifique avec les essais non destructifs par ordinateur (dans les industries automobiles par exemple), de la théorie du signal (dans les industries de télécommunication), de la théorie du krigeage[54] en géostatistique et de la simulation des gisements dans les industries pétrolières sont aujourd’hui des théories ayant des fondements essentiellement mathématiques.
Le développement de la théorie des ondelettes[55] avec Meyer a pris le dessus sur la théorie de Fourier[56] pour devenir un outil de travail nouveau et performant dans les compagnies pétrolières et le traitement des signaux. Il y a de nombreux autres exemples de théories mathématiques fondamentales qui ont donné lieu à des applications (Perrin, 2004) :
-
les nombres premiers et le chiffrement Rivest – Shamir – Adleman (RSA);
- les imaginaires et leur utilisation en électricité;
- la géométrie riemannienne et la relativité;
- les espaces de Hilbert et la mécanique quantique;
- la logique et l’informatique;
- le mouvement brownien et la finance.
Dans le domaine des finances et de l’actuariat, les techniques probabilistes et statistiques connaissent un véritable engouement aujourd’hui dans la gestion prévisionnelle de l’assurance, de la banque et de la finance (Le Borgne, 1995). L’actuaire utilise des outils mathématiques comme les tests d’hypothèses ou d’efficacité pour estimer au plus juste degré, dans un contexte des marchés de plus en plus concurrentiels, les risques liés à un contrat d’affaires, à une campagne commerciale, au lancement d’un nouveau produit. Dans le cadre d’un contrôle de gestion ou d’inspection, les théories d’échantillonnage pourraient être sollicitées. Au cours des vingt dernières années, l’on a pu observer les bouleversements des systèmes financiers de par le monde. La crise bancaire et financière de 2008 ayant considérablement affecté les économies d’un certain nombre de pays puissants, les spécialistes de la finance ont été contraints de revoir leurs modèles en accordant encore plus de place à l’efficience des outils mathématiques[57].
Au total, un certain nombre d’évolutions sont en cours ou vont s’imposer, aussi bien dans les pratiques en vigueur qu’en ce qui concerne la formation. Les formateurs sont notamment amenés à mettre l’accent sur les statistiques, et à faire travailler les étudiants sur une vision du risque quantitatif global. Cet aspect est désormais central. Certains enseignements ont été renforcés : la régulation, le risque du marché. (El Karoui, 2013, paragr. 17).
De même, le secteur industriel a besoin d’un nombre sans cesse croissant de mathématicien·ne·s et non plus seulement d’ingénieur·e·s, car à un niveau élevé, l’activité industrielle est bien plus proche de la recherche. Que ce soit dans le domaine de la production de l’énergie, celui de l’aéronautique, de la production pétrolière ou même celui de la pharmacie, les modèles mathématiques sont présents. Pour de Rocquigny, « la coopération idéale, c’est quand des mathématiques innovantes sont mises au service d’une vraie question industrielle. Cela suppose que l’entreprise accepte de transmettre aux chercheurs ses véritables données » (cité par Lucas, 2011, paragr. 2).
Le secteur de l’environnement quant à lui développe également un besoin important de spécialistes en botanique, en chimie et même en géographie imprégnées de mathématique. Ces personnes cherchent à améliorer les programmes de traitement des déchets toxiques, à étudier la vitesse de dégradation de la couche d’ozone afin de réduire ses effets sur la faune et de la flore et d’optimiser les programmes de gestion des problèmes d’urbanisation. Les travaux de l’équipe MPE évoqués plus haut sont assez éloquents à ce sujet. On y trouve des résultats d’études sur la dynamique de la fonte des glaces, la mesure de la variation des précipitations et sur la modélisation mathématique du paludisme en rapport avec le changement climatique entre autres (Kaper & Roberts, 2019). Concernant le paludisme et d’autres épidémies, les travaux réalisés par Kamgang (2003) sur les modèles épidémiologiques montrent à suffisance le rôle central des mathématicien·ne·s dans la recherche des solutions aux problèmes de santé humaine[58].
L’on remarque également aujourd’hui que l’activité mathématique n’est pas seulement destinée à l’enseignement. Elle est en train de devenir une affaire très rentable (Mela, 1993). À travers sa branche informatique par exemple, les mathématiques avec l’intelligence artificielle développent des techniques comme la construction des systèmes experts pour rester davantage au service des autres disciplines. De nouveaux outils essentiellement informatiques accompagnent désormais l’homme dans ses diverses actions journalières. Il ne s’agit pas seulement des encyclopédies, mais surtout des outils mathématiques tels que les algorithmes, les applications pour aider les machines à « raisonner ».Ces innovations technologiques globalement appelées « e-services » se distinguent dans leur dénomination par les préfixes e– pour electronic, i– pour intelligent ou m– pour mobile qui précèdent généralement leurs dénominations. C’est ainsi que l’on a des e-mail (courrier électronique), e-health (télémédecine), e-voting (vote électronique), i-voting (vote par internet ou vote en ligne), e-commerce (commerce électronique ou en ligne), e-business, e-government (administration en ligne), e-book (livre électronique), m-learning (pour faciliter les études aux apprenant·e·s qui pourront désormais accéder à des bibliothèques via l’électronique), m-voting (vote par téléphone mobile), e-whiskers ou e-moustaches (des capteurs pouvant permettre à des robots de se mouvoir dans des milieux avec obstacles), e-profile (comportement ou image en ligne). Bref, des e-services pour une e-société.
Des structures comme les centres d’étude et apprentissage des mathématiques, le « mathematics learning centre » et les cabinets de « consulting » en mathématique (Mela, 1993) existent dans certains pays avancés. Ils connaissent déjà une expansion à travers d’autres pays en voie d’émergence dans le monde. Ce sont des sortes de cabinets-conseils spécialisés en sciences mathématiques qui offrent aux publics divers services comme le coaching en mathématiques, le traitement et l’analyse des bases de données, la programmation linéaire ou complexe, l’économétrie, la formation en informatique et même les cours de soutien. Entre-temps, les fameux « répétiteurs » de mathématiques font d’assez bonnes affaires auprès des parents d’élèves. Au Kamerun par exemple, de jeunes et ancien·ne·s étudiant·e·s des filières scientifiques s’organisent en groupes d’étude pour préparer, à faible coût pendant un ou deux mois, leurs jeunes frères et sœurs aux concours d’entrée dans certaines facultés et grandes écoles du pays.
Compte tenu des grandes possibilités qu’offrent les mathématiques, il est certain que son champ d’action est incroyablement vaste, bien vivant et très fécond. On comprend dès lors que cette discipline est une ressource intellectuelle et stratégique non épuisable pourvu que l’on sache la cultiver, l’entretenir et la transmettre aux générations futures. Elle est même dotée de valeurs écologiques sur lesquelles il faudrait compter pour amorcer la voie d’un développement inclusif et durable. Pour nous, deux cas de figure pourraient se poser à l’Afrique. D’une part, il y a le manque de ressources humaines (mathématiciens et mathématiciennes) dans un contexte où les sujets de réflexion en mathématiques foisonnent. Le rapport de 2017 de la Fondation pour le renforcement des capacités en Afrique souligne un manque de professionnels dans les disciplines des sciences et des mathématiques : « L’Afrique connait un déficit de 4,3 millions d’ingénieurs et 1,6 million de scientifiques et de chercheurs en agriculture. » (ACBF, 2017 : 9); d’autre part, l’emprise grandissante des sciences, avec ses nouvelles applications technologiques, sur nos modes de vie sans que nous n’ayons de contrôle ni sur leur chaine de production ni sur les effets potentiellement nocifs qu’elles peuvent avoir vis-à-vis de nos sociétés, nos cultures et nos traditions. Il devient évident que le déficit de mathématicien·ne·s aggrave la difficulté à examiner des problèmes mathématiques qui pourraient affecter de façon significative les problématiques de développement de l’Afrique. Un choix efficient de l’orientation de la recherche devrait permettre à l’Afrique de mener une réflexion de nature scientifique et éthique nécessaire pour repérer et repousser les limites de cette emprise.
Au terme de ce chapitre, nous avons essayé de situer les mathématiques dans l’univers complexe de la connaissance en faisant ressortir ses caractères subtils et incontournables : subtils, parce que les mathématiques sont une discipline dotée d’une langue et des objets singuliers élaborés de manière ingénieuse; incontournables parce qu’elles sont au cœur de la vie humaine et elles servent de modèles aux autres disciplines scientifiques. En fait, les mathématiques sont une discipline qui se renouvelle de manière permanente et qui s’enrichit au contact de la société et des sciences diverses. La connaissance de cette discipline n’est jamais totalement épuisée; et parmi ses nombreux résultats, certains attendent encore de trouver des applications quand ils ne sont pas simplement abandonnés (Dyson, 1972). Si la plupart des pays européens, d’Amérique et d’Asie, suite aux progrès scientifiques et technologiques soutenus par de grandes recherches se sont développés au lendemain des deux grandes guerres mondiales, ceux de l’Afrique gagneraient à s’efforcer de rattraper leur retard, et, pourquoi pas les dépasser. Pour y parvenir, il faut sans doute se débarrasser d’un certain nombre de préjugés et de complexes. Le travail de transformation des représentations négatives en images positives devra cibler prioritairement les jeunes; ceux-là et celles-là mêmes qui sont des féru·e·s de nouvelles technologies – amplifiées par les outils mathématiques – mais en même temps réfractaires aux mathématiques. La question cruciale ici est : qu’est-ce qui dans l’environnement et le milieu de vie des jeunes Africain·e·s peut favoriser l’éclosion des mathématiques, de sorte à produire un impact pouvant améliorer leurs conditions de vie et celles de leur communauté?
- Ce mot est utilisé par Srinivasa Rao pour désigner cette sorte de science occulte, les mathématiques ésotériques qui exigeraient que l’on soit magicien·e ou sorcier·e pour les comprendre et les pratiquer. ↵
- "Pure mathematics is an immense organism built entirely and exclusively of ideas that emerge in the minds of mathematicians and live within these minds." ↵
- Muhammad ibn-Musa Al-Khwarizmi, un des plus éminents savants arabes du moyen âge qui a traité des applications concrètes du système numéral décimal et qui a clarifié en la simplifiant, la résolution de certains problèmes mathématiques de l’époque. La simplicité des chiffres arabes est évidente : le nombre CLXXXVII (en chiffres romains) s’écrit 187 (en chiffres arabes). Les communautés peules d’Afrique comptent traditionnellement dans le système numéral de base 5. ↵
- "What’s more, with Al-Khwarizmi’s algebra, these scholars provided us with the single most important mathematical tool ever devised, and one that underpins every facet of science, as well as more everyday processes." ↵
- Ce titre en français est donné comme équivalent de l’arabe Al-Kitab al mukhtasar hisab al-jabr wal-muqabala, d’après la traduction de Jean-Pierre Levet (1997), faite à partir de la traduction latine de Robert Chester. Cf. univ-irem.fr/spip.php?article1274. Pour d’autres informations sur ce savant arabe, voir Greenwald & Thomley, 2012 : 32-33. ↵
- En français moderne, « La sagesse ne peut entrer dans un esprit méchant, et science sans conscience n’est que ruine de l’âme ». Adaptation tirée de la-philosophie.com/science-sans-conscience. ↵
- De nombreux·ses élèves et mêmes certain·e·s enseignant·e·s trouvent encore aujourd’hui et à tort, en cette inscription, une sorte de ségrégation ou de discrimination des scientifiques par rapport aux littéraires. Pourtant Platon, qui en est l’auteur est une figure littéraire qui parle aisément de la géométrie. Pour lui, le géomètre c’est la personne qui, dans son raisonnement, procède par une démarche mathématique : logique, rigueur et systématicité. Ces exigences d’ordre mathématique ou géométrique existent et s’appliquent également avec beaucoup de succès dans les disciplines dites littéraires et apparentées. ↵
- Il s’agit de l’égalité de trois fractions : AC : CB = AD : DC = CE : EB, qui, mathématiquement parlant, traduisent l’existence d’un même rapport de proportionnalité entre les différents segments [AC] et [CB], [AD] et [DC], puis [CE] et [EB] respectivement, isssus des trois opérations de segmentation successives de la ligne (AB). ↵
- Stéréométrie : application pratique de la géométrie à la mesure des solides naturels (cubage, jaugeage, métrage). Définition Le petit Robert, édition 1993. ↵
- Les écrits en gras et les soulignements sont de l’auteur. ↵
- Cf. figure 2 plus haut. ↵
- Il faut cependant relativiser cette hiérarchisation platonicienne au regard de l’évolution des sciences. On peut bien rapprocher les objets mathématiques contemporains des idées de Platon. Sur ce point, voir par exemple la première note de la page XLIV de Baccou (1936). ↵
- C’est nous qui soulignons. ↵
- Roger Martin, logicien français qui contribua à l’introduction de la logique contemporaine dans l’Université française. Propos tenus lors du colloque consacré à Bachelard, Cerisy, 1970. ↵
- On peut considérer que l’absence de contradictions est un atout pour la discipline mathématique par rapport à ses propres principes. Cela reste donc valable pour la discipline. En dehors de ce cadre, les contradictions ne sont pas du tout considérées comme des tares ou des défauts. Elles font partie intégrante des systèmes et de la vie humaine. C’est d’ailleurs, le problème posé par Wittgestein dans sa réflexion sur le langage humain qu’il trouve imparfait comparé au raisonnement logique. ↵
- C’est-à-dire une description cohérente et rigoureuse de la réalité et même « des expériences qui n’ont jamais, de toute éternité, été réalisées. » (Ienna, 2019, paragr. 22). ↵
- Cf. feglossary.sil.org/fr/page/definitions-key-terms-theory-enunciative-operations?language=fr. Pour plus de détails sur la notion de métalangage, on peut se rapporter à Rey-Debove, 1985. ↵
- Voir la page personnelle de Jean-Louis Sigrist, Url : jlsigrist.com. ↵
- Ce sont les auteur·e·s qui soulignent. "In the realm of ideas, of mental objects, those ideas whose properties are reproducible are called mathematical objects, and the study of mental objects with reproducible properties is called mathematics." ↵
- Il s’agit d’une formule qui met en relation cinq constantes mathématiques spéciales à l’aide de trois opérations arithmétiques. ↵
- Encore appelée analyse dimensionnelle, il s’agit d’une méthode pratique permettant de vérifier les unités et l’homogénéité d’une formule. ↵
- Sur cette sériation des problèmes, nous nous sommes inspirés non seulement des travaux des mathématicien·ne·s (Chevellard, 1998; Guisti, 1999), mais aussi de ceux du linguiste (Culioli, 1990). ↵
- Sur l’origine historique de l’induction en mathématiques, on se rapportera aux travaux de Rashed (1972). ↵
- L’étape d’initialisation consiste à établir qu’une propriété dépendant d’un paramètre entier est vraie à un premier niveau; l’hérédité consiste à supposer que si la propriété est vraie à un niveau, c’est qu’elle est vraie au niveau suivant. Enfin, la validation désigne la phase de généralisation que la propriété est vraie à tous les niveaux à partir du premier niveau. ↵
- Nous donnons ici quelques éléments définitionnels à titre indicatif. Pour plus de précision et des illustrations, voir la section 2.2.3. ↵
- C’est nous qui soulignons. ↵
- Elle est née au XIXe siècle et a été développée par le cercle de Vienne et le néopositivisme. ↵
- Il s’agit de l’égocentrisme (difficulté de se placer au point de vue d’autrui), du syncrétisme (tendance à percevoir par une vision globale sans analyse, incapacité de structurer sa perception, d’associer les parties d’un tout), de la transduction (méthode de raisonnement propre aux enfants, qui part du singulier au singulier, et qui ne constitue ni une induction ni une déduction), de l’irréversibilité de la pensée (incapacité de remonter sa pensée en arrière, de lire la conservation des quantités). Voir par exemple Quentel (1997) et Reginensi (2004). ↵
- La théorie des Opérations énonciatives de Culioli (1990), ainsi que les grammaires dites cognitives (Langacker, 1999) et la théorie du prototype de Rosch (1983) s’en ont bien inspiré. ↵
- C’est l’auteur qui souligne. ↵
- Les majuscules sont de l’auteur. ↵
- L’italique est de l’auteur. Pour plus de détails, voir Philonenko (2004 : 72-74). ↵
- Un exemple de règle pragmatique est la règle de dépendance des variables. Voir Durand-Guerrier (2005 : 139). ↵
- Localité de la région de l’Adamaoua, située à environ 180 km de la ville de Ngaoundéré. ↵
- Pour cette section, nous nous sommes inspirés largement du rapport 1992 du Centre national de la recherche scientifique (CNRS) qui consacra de nombreuses lignes à la définition des enjeux de l’enseignement des mathématiques. Voir Rapport du CNRS (1993 : 14-15). ↵
- "If mathematics education at school is the answer, what was the question? What is the primary goal of mathematics education at schools? My claim will be that: (a) It is not one goal but at least three; and (b) These goals are moving targets." ↵
- "the questions haven’t changed fondamentally by the time our answers are being implemented." ↵
- Propos recueilli par l'auteur le 15 mars 2015 lors d’un entretien avec cet enseignant-chercheur de l’Université de Ngaoundéré (Kamerun). ↵
- Il s’agit des 23 « problèmes de Hilbert » présentés par le mathématicien David Hilbert lors du deuxième congrès international des mathématiciens tenu à Paris en août 1900, qui devaient, selon lui, marquer le cours des mathématiques au xxe siècle. ↵
- Très récemment en 2004, les mathématiques non commutatives ont connu un grand boom dans le cadre de leur application. ↵
- Gabriel Nguetseng, mathématicien camerounais, qui en qualité de précurseur a introduit et apporté des contributions fondamentales à la théorie d’homogénéisation avec ses nombreuses applications. ↵
- https://www.journaldunet.com/management/emploi-cadres/1099814-les-meilleurs-metiers-de-2014-et-les-pires/1099816-les-20-meilleurs-metiers. ↵
- De nombreux sites présentent « L’histoire des Mathématiques » et parlent de la culture mathématique. Par exemple, le site www.youtube.com/watch? pour des vidéogrammes; RTS Découverte avec la collaboration de Dominique Arlettaz, professeur de mathématiques à l’Université de Lausanne, explore l’origine des mathématiques et leur évolution. ↵
- Cadre servant à délimiter ou circonscrire une famille de situations de vie et des exemples pour lesquelles un programme d’enseignement vise à former l’élève, à l’intérieur d’un module (IGE-MINESEC, Yaoundé). ↵
- C’est-à-dire très variables, changeant avec des paramètres liés ou non à une influence humaine. ↵
- Les conditions aux limites constituent des techniques de résolution d’équations différentielles et d’équations aux dérivées partielles mises en place par Dirichlet et Neumann. Sur la définition, cette notion ainsi que la contribution de ces mathématicien·ne·s, on peut consulter Gowers et al. (2008) et Fischer (1994). ↵
- Voir https://unesdoc.unesco.org/ark:/48223/pf0000265647 ↵
- La culture est comprise ici comme l’ensemble des connaissances acquises dans des domaines divers et spécifiquement dans le domaine des sciences et des mathématiques. On parle alors d’une culture mathématique. Quant à la paix, elle compte parmi les questions pour lesquelles la recherche en mathématique a apporté de nombreuses solutions, notamment dans le domaine militaire : armement, tactiques militaires, renseignements. ↵
- ‟Student in the MPE [Mathematics of Planet Earth] CDT (Centre for Doctoral Training) will receive cohort-based Ph D. training in the mathematical and computational technics needed to understand predict and quantify risk and uncertainty for extreme weather and climate change.” ↵
- Il s’agit d’une organisation africaine consacrée au développement des mathématiques en Afrique, fondée en 1976 à Rabat au Maroc, lors du 1er congrès panafricain des mathématiciens, avec comme 1er président le Camerounais Henri Hogbè Nlend. En 1986, cinq commissions sont créées au sein de cette structure : la commission en charge de la question des femmes africaines en mathématiques; la commission en charge de l’éducation mathématique en Afrique; la commission en charge de l’histoire des mathématiques en Afrique; la commission en charge de la recherche et de l’innovation; et la commission en charge des olympiades panafricaines de mathématiques. Voir www.africamathunion.org. ↵
- C’est un vaste programme de recherche transdisciplinaire et transculturelle en histoire et philosophie des mathématiques. ↵
- Traduction de : « We will call ethnomathematics the mathematics which is practised among identifiable cultural groups, such as national-tribal societies, labor groups, children of a certain age brackets, professional classes, and so on. » ↵
- Edward Witten, mathématicien-physicien américain, lauréat de la médaille Fields en 1990. ↵
- Du nom de son inventeur Daniel Gerhardus Krige (1919-2013), ingénieur minier sud-africain, précurseur dans le champ de la géostatistique. ↵
- La transformée en ondelettes est une méthode mathématique développée dans les années 1980 par Yves Meyer, fondée sur un ensemble de fonctions de base différentes des fonctions sinusoïdales utilisées dans la méthode de Fourier, qui remplace avantageusement la transformée de Fourier dans certaines situations. À travers le standard international JPEG-2000 pour la compression d’images, ces ondelettes ont actuellement envahi tous les domaines de l’image, de l’internet aux appareils photos numériques et se dirigent vers les satellites. ↵
- Jean Joseph Fourier (1768-1830), mathématicien français connu pour la découverte des séries trigonométriques qui portent son nom, les séries de Fourier. Il utilisa ces séries pour exprimer toutes fonctions continues ou discontinues comme somme d’une série infinie de fonctions sinus et de cosinus de la forme sin(ax) ou cos(ax), chacune affectée d’un certain coefficient. ↵
- Pour minimiser les risques d’explosion des modèles mathématiques, il convient de souligner la nécessité d’introduire dans le cours initiation à la recherche en mathématiques (niveau master et plus), la notion d’éthique et la responsabilité de la recherche vis-à-vis de la société. Cette question peut très bien être intégrée au concept de justice cognitive que nous avons abordé dans la sous-section 1.3.1. ↵
- De nombreux travaux ont été réalisés au Cameroun sur cette question. Békollè (2019) en donne un aperçu historique et synthétique. ↵

