12 Mary Boole et ses cinq filles (1832–1916)
Philippe Etchecopar

http://www.agnesscott.edu/lriddle/women/boole.htm
André Breton aurait organisé une quête pour la veuve du soldat inconnu sous prétexte qu’elle était encore plus inconnue que son célèbre mari! Nous pourrions ajouter que la femme d’un illustre savant, même savante elle-même, reste une grande inconnue, elle n’est que la femme cachée par l’ombre d’un grand homme!
Ainsi, récemment, Google célébrait le bicentenaire de la naissance de Georges Boole, un logicien anglais qui a donné son nom à sa découverte de l’algèbre dite « booléenne », cette découverte ayant été essentielle au développement de l’informatique. Georges Boole était un cas particulier dans le monde des sciences du début du XIXe siècle. Il venait d’une famille pauvre, n’était pas passé par les universités prestigieuses et était autodidacte. À 16 ans il avait appris seul le latin, le français, l’italien et l’allemand, si bien qu’il obtient un poste d’instituteur en dépit de sa jeunesse. Comme instituteur, il développa de multiples méthodes pour amener les élèves à « comprendre » plutôt qu’à « se souvenir », ce qui l’amena à s’intéresser au fonctionnement de la pensée. À 18 ans, il se lança dans les mathématiques en lisant Newton et Lagrange, si bien qu’à 19 ans il fonda sa propre école. Il publia ses premiers travaux d’algèbre et reçut à trente ans la prestigieuse médaille de la Royal Society. Il avait découvert une algèbre binaire, des 0 ou des 1, des vrais ou des faux, qui permettaient de mettre en équations des raisonnements logiques et de les résoudre. Il publia « Les lois de la pensée » qu’il a dédié à sa femme pour sa collaboration et qui définit l’algèbre booléenne, une branche majeure des mathématiques. Une section de ce livre porte sur les différentes preuves de l’existence de Dieu! Sa formation autodidacte le poussait à chercher des liens entre différentes disciplines. Son ambition était, déjà, de mathématiser la pensée! Il s’interrogea sur la liberté et l’imprécision de la pensée, par rapport à la rigueur des lois logiques. En attendant, cette algèbre a permis de mettre en équations les circuits électriques, ce qui a jeté les bases de l’informatique qui travaille en binaire sur des circuits électriques. On comprend l’hommage de Google à l’un des pères de l’informatique, mais il ne faut pas perdre de vue que l’héritage de Boole va au-delà d’une suite de 0 et de 1!
Dans toutes les biographies de Boole, sa femme est à peine mentionnée comme la mère de leurs cinq filles qu’elle a par ailleurs élevée seule, Boole étant décédé très jeune. Or, cette femme, Mary Boole, a elle-même été une mathématicienne majeure qui a découvert une nouvelle géométrie et qui a surtout révolutionné à l’époque, la fin du XIXème siècle, l’enseignement des mathématiques aux enfants, allant souvent à contre-courant de l’enseignement traditionnel des mathématiques dans la société victorienne.
Fille de pasteur
Pourtant, toute jeune, sa vie sortait déjà de l’ordinaire. Fille du pasteur Thomas Everest, elle garda de lui l’idée de porter la bonne parole, un souci pour « l’âme » et un langage volontiers messianique. Elle hérita aussi d’un certain mysticisme. De plus, son père répétait que le but d’un système de santé était de prévenir plutôt que de guérir et il prônait l’homéopathie dont Mary se fit toujours la défenderesse. Par ailleurs, son oncle Georges Everest était un géographe qui laissa son nom au mont Everest pour avoir arpenté le nord de l’Inde et l’Himalaya. Élevée d’abord en France, elle développa un goût peu ordinaire pour les mathématiques. Elle prit des cours particuliers, car pour une jeune fille, la seule étude tolérée était celle de la Bible et les seules sciences accessibles étaient les sciences ménagères. Son tuteur, un certain M. Deplace, disciple des théories de l’éducation de Jean-Jacques Rousseau, la marqua profondément. Pour Jean-Jacques Rousseau la clé de l’enseignement était d’encourager la curiosité naturelle des enfants, de respecter leur rythme et de les guider pour qu’ils apprennent par eux-mêmes. Notons au passage que Rousseau ne voyait toutefois pas la nécessité pour une fille de faire des études…
Femme de George Boole
À son retour en Angleterre, elle avait 20 ans, Un ami de son oncle Everest, le mathématicien Georges Boole, devint son tuteur, puis, à la mort de son père qui la laissa sans dot, il devint son mari. Elle partageait plusieurs préoccupations avec Georges, dont celle de savoir comment amener les élèves à comprendre, à collaborer et à se passionner plutôt qu’à retenir et à vouloir être les meilleurs et accéder à l’élite. Ensuite, elle s’interrogeait sur les liens entre la science et la religion et partageait la passion de Georges pour une certaine mathématisation de la pensée, d’où leur intérêt commun pour la psychologie. Ses préoccupations religieuses sur le sens de la vie, héritées de son père, l’amenèrent à correspondre avec Darwin sur la nature humaine et les liens entre l’existence de Dieu et la théorie de l’évolution. Ci-dessous un passage de leur correspondance :
Le 13 décembre 1866, lettre de Mary Boole à Darwin :
Dear Sir,
Will you excuse my venturing to ask you a question to which no one’s answer but your own would be quite satisfactory to me.
Do you consider the holding of your Theory of Natural Selection, in its fullest & most unreserved sense, to be inconsistent,—I do not say with any particular scheme of Theological doctrine,—but with the following belief, viz:
That knowledge is given to man by the direct Inspiration of the Spirit of God.
That God is a personal and Infinitely good Being.
That the effect of the action of the Spirit of God on the brain of man is especially a moral effect.
And that each individual man has, within certain limits, a power of choice as to how far he will yield to his hereditary animal impulses, and how far he will rather follow the guidance of the Spirit Who is educating him into a power of resisting those impulses in obedience to moral motives.
I felt that you had supplied one of the missing links,—not to say the missing link,—between the facts of Science & the promises of religion. Every year’s experience tends to deepen in me that impression.
I remain, Dear Sir, Yours truly. Mary Boole
Darwin lui répondit le lendemain, le 14 décembre 1866 :
Dear Madam,
It would have gratified me much if I could have sent satisfactory answers to yr. questions, or indeed answers of any kind. But I cannot see how the belief that all organic beings including man have been genetically derived from some simple being, instead of having been separately created bears on your difficulties.— These as it seems to me, can be answered only by widely different evidence from Science, or by the so called “inner consciousness”. My opinion is not worth more than that of any other man who has thought on such subjects, & it would be folly in me to give it; I may however remark that it has always appeared to me more satisfactory to look at the immense amount of pain & suffering in this world, as the inevitable result of the natural sequence of events, i.e. general laws, rather than from the direct intervention of God though I am aware this is not logical with reference to an omniscient Deity— Your last question seems to resolve itself into the problem of Free Will & Necessity which has been found by most persons insoluble.
I have the honor to remain, dear Madam, éyours very faithfully. Charles Darwin.
En plus de partager ces préoccupations sur les liens entre les mathématiques et la pensée, sur les liens entre la religion ou la psychologie et la science et les théories de l’éducation, ils eurent cinq filles en neuf ans.
Georges décéda en 1864. Il était rentré de l’université trempé par une pluie glacée, il pensait, comme Mary, que l’on combattait le mal par le mal : elle l’aspergea donc régulièrement d’eau glacée, cela ne marcha pas et il en mourut. Au final, sans le vouloir, la notoriété de Georges Boole aura laissé Mary dans l’ombre, comme d’ailleurs la notoriété due aux 0 et 1 aura écrasée le reste de son œuvre.
Mère de cinq filles
Mary Boole se retrouva seule à élever ses cinq filles, qui eurent une vie hors de l’ordinaire :
- Mary Ellen qui épousa le mathématicien et philosophe Charles Hinton. C’est le grand philosophe de l’hyperespace et il fut le pionnier de l’espace à quatre dimensions. Son biographe indique qu’il proposait que notre espace possède une légère épaisseur dans la quatrième dimension nous permettant de construire des pensées 4D. Accusé de bigamie, il se réfugia au Japon en 1886;
- Margareth, qui épousa le peintre Edward Ingram Taylor, fut la mère du physicien Geoffrey Taylor qui participa au projet Manhattan;
- Alicia, sur laquelle nous reviendrons et qui devint elle-même mathématicienne;
- Lucy, première femme professeur de chimie au Royal Free Hospital de Londres, demeura célibataire et resta avec sa mère;
- Ethel, écrivaine, musicienne et suffragette, épousa un révolutionnaire bibliophile, Wilfrid Voynich, celui qui a découvert le fameux « Manuscrit de Voynich » écrit à partir d’un alphabet jamais déchiffré. Elle fut célèbre pour son roman « The Gadfly » qui raconte un combat révolutionnaire en Italie. Ce livre devint un bestseller en Union soviétique, où il fut vendu en 2 500 000 exemplaires, ainsi qu’en Chine. Il fut adapté au cinéma par Alexandre Feinzimmer en 1955, puis adapté une seconde fois en 1980 par Nikolai Machtchenko; la musique fut composée par Chostakovitch (The Gradfy, opus 97).
L’enseignement des sciences
Mary se retrouva donc seule pour éduquer ses filles. Ses passions majeures étaient les mathématiques et l’enseignement des sciences. De par sa formation, elle avait une vision globale du monde et elle était poussée par une quête spirituelle, voir mystique, intense. Mais nous étions en pleine ère victorienne et à cette époque l’enseignement supérieur était fermé aux femmes, et aussi aux juifs. Pour gagner sa vie, elle ne put trouver qu’un poste de bibliothécaire au Queens College à Westminster, le premier collège pour filles. En fait, sa réputation se répandit vite et les élèves défilaient à la bibliothèque pour se faire expliquer ce qui leur était enseigné en cours. Ses talents exceptionnels de pédagogue furent même reconnus par la direction de la London Board of Education.
Ses principes pédagogiques découlaient de « L’Émile » de Jean-Jacques Rousseau, et de sa propre expérience avec son tuteur, M. Deplace. Ils découlaient aussi de sa conception religieuse de la nature humaine. Il fallait développer la passion d’apprendre et un esprit d’entraide chez les enfants :
Seules des mathématiques mortes peuvent être enseignées dans un esprit individuel de compétition. Des mathématiques vivantes doivent toujours être un bien commun (d’après Eleanor Meredith Cobham, Mary Everest Boole: Collected Works [1931], 40).
Dans son livre Philosophy and fun in algebra, elle explique la nécessité d’établir des liens entre les mathématiques et la vie. Elle commence toujours ses explications par des petites histoires puis établit des liens avec la littérature et la philosophie. Ainsi, elle multiplie les discussions informelles sur l’hébreu, les droits des animaux, la logique, l’évolution, la psychologie et bien d’autres choses… Dans ses cours elle « fait un peu de théâtre » pour capter l’attention des enfants. À cet effet, elle adopte le ton mystique qu’on utilise pour raconter les grandes épopées. Elle insiste beaucoup sur le travail coopératif, incite les élèves à partager leurs idées et à faire preuve de créativité et d’esprit critique. En ce sens, elle amenait les élèves à se poser des questions et à tenir un journal sur leurs réflexions. Elle accorde de l’importance aux expériences pratiques, aux manipulations d’objets concrets pour amener les enfants à prendre conscience de la nature des concepts mathématiques et à mieux les comprendre. Pour elle, peut-être à la différence de George, les concepts mathématiques, comme ceux de l’arithmétique, existent concrètement.
Par exemple, pour permettre aux enfants d’apprendre la géométrie et l’analyse en expérimentant par eux-mêmes, elle développe une nouvelle approche concrète, la géométrie dite « curve stitching » ou dite « des ficelles ». Avec des ficelles, des ciseaux, des règles et des crayons, cette géométrie propose quelques règles simples de construction pour développer des figures de simples à complexes qui permettent de découvrir par soi-même des propriétés de la géométrie ou du calcul différentiel. Par exemple sur la figure ci-dessous en joignant, dans l’ordre des points horizontaux aux points verticaux, on voit apparaître une courbe primitive, une vision d’une intégrale…

Ce principe permet d’obtenir simplement des figures complexes :
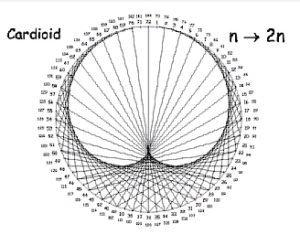
Cela permet une compréhension concrète et une manipulation de concepts géométriques comme les angles, les multiples formes de polygones, etc. Cette méthode « pas à pas » aurait été bien adaptée à l’utilisation de l’informatique en mathématiques.
À défaut d’ordinateur, pour développer plus modestement cette approche, Mary Boole proposait du tissus, des ciseaux, une aiguille et du fil! Les schémas, recouvrant des bouts de tissus, permettaient ainsi de beaux motifs de couture. On comprendra qu’à l’époque victorienne, c’était un moyen d’intéresser les filles aux sciences…
De multiples exemples de constructions géométriques possibles avec cette approche se retrouvent aujourd’hui sur le web, particulièrement sur YouTube. En entrant « Mary Boole », on obtient de bonnes présentations de ses approches pédagogiques, tandis qu’en entrant « curve stitching » on dispose d’un grand nombre d’exemples de la géométrie établie par Mary Boole.
À travers tous ces exemples on s’aperçoit que cette méthode débouche sur un véritable art, un peu comme on assiste aujourd’hui avec la géométrie fractale de Mandelbrot. Intéressée par le spiritisme, qui rencontrait un certain succès à la fin du XIXème siècle, comme chez Victor Hugo ou Conan Doyle, Mary Boole publia The Message of Psychic Science for Mothers and Nurses, ce qui lui valut des ennuis avec les autorités académiques et elle perdit son poste.
Elle écrivit aussi Logic taught by love, The message of psychic science to the world, The preparation of child to science, Suggestions for increasing ethical stability, The mathematical psychology of Gratry and Boole translated from the language of the higher calculus into that of elementary geometry.
Pacifiste et libertaire
Si ses convictions morales et religieuses ont été à l’origine de ses principes pédagogiques, elles ont aussi été à la source de ses convictions sociales et politiques. Elle a ainsi été très proche du philosophe anarchiste Charles William Daniel (1871-1955). Il était un pacifiste convaincu et, avec Mary Boole, ils avaient créé The London Tolstoyan Society dans la ligne de Tolstoï, l’auteur de « Guerre et Paix » et pacifiste renommé du début du XXème siècle. Ils ont créé une maison d’édition, Free Age Press, pour rendre accessibles Aristote, Rousseau, Proudhon, etc. Ils ont aussi édité une revue, The Crank. Ce nom, « manivelle » en français, a été choisi par Mary Boole car elle disait « que c’était un petit appareil, mais qui faisait des révolutions »! The Crank était aussi le nom du restaurant où les membres de la London Tolstoyan Society, des intellectuels, des artistes, des journalistes, se réunissaient. Charles William Daniel était aussi, comme Mary Boole, un végétarien militant, il ne votait jamais. Il batailla aussi contre la conception autoritaire du socialisme dominante au début du XXème siècle. Comme Mary Boole, il était aussi un adepte des médecines alternatives.
Mary Boole a passé le reste de sa vie à écrire des livres sur l’éducation et à participer à des débats sur de nombreux thèmes, tant au niveau de l’enseignement, des mathématiques qu’au niveau des enjeux sociaux comme l’opposition à la Première Guerre mondiale. Ainsi, son livre La préparation de l’enfant pour les sciences, écrit en 1904, a eu un impact important sur le développement des écoles primaires, tant en Angleterre qu’aux États-Unis. Elle a aussi publié des livres sur des sujets controversés dans les milieux scientifiques comme Mathématiques en occultisme.
Elle est décédée en 1916.
Alicia Boole Stott, une des filles de Mary
Suivant les principes de sa mère, Alicia étudie à son rythme, sans trop de contraintes. Comme ses sœurs, une bonne partie de son éducation se fait par des discussions avec sa mère et les amis de celle-ci, dont Charles Darwin et HG Wells. Et aussi James Hinton, un chirurgien, dont le fils Charles était passionné de philosophie et de mathématiques et allait devenir le beau-frère d’Alicia. Influencée par les travaux géométriques de sa mère et par ceux de James Hinton sur la géométrie de dimension 4, elle se passionne à son tour pour cette géométrie de dimension 4, plus particulièrement les polytopes.
Au départ, un polyèdre est un solide géométrique dont les faces sont des polygones plats. Si ses faces sont toutes identiques et si chaque sommet a le même nombre d’arêtes, on dit que le polygone est « régulier ». En fait depuis les grecs, on sait qu’il en existe neuf, appelés aussi « les solides de Platon ».
Un polytope est un polyèdre régulier, mais dans l’espace à quatre dimensions.
Imaginer des objets dans des espaces à quatre dimensions, ou de dimensions plus élevées est difficile, sauf pour un mathématicien habitué à travailler dans des espaces à n dimensions : il lui suffit de remplacer n par 4… . C’est vouloir visualiser ce concept qui est ardu. Or, Alicia Boole possédait cette rare capacité.
Par exemple, Charles Hinton, son beau-frère, a défini un cube à quatre dimensions, un « tesseract » composé de 16 sommets, 32 arêtes et 8 faces cubiques, soit 24 faces pleines, chacune des faces du tesseract étant un cube. Ce qui, traduit de l’imagination d’Alicia Boole pourrait donner dans un espace à deux dimensions :
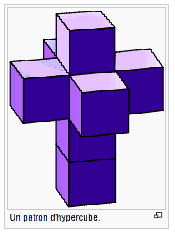
Etienne Ghys résume ainsi les découvertes d’Alicia Boole en la qualifiant « d’héroïne de la quatrième dimension » :
Elle finit par comprendre la nature précise des polyèdres réguliers de dimension quatre. Il y en a six, dont l’un s’appelle l’hexacosichore (car il a 600 faces) et possède 14 400 symétries. L’étude des symétries est au cœur des mathématiques. Alicia s’aide de modèles en carton, en suivant les préceptes de sa mère …
L’imagination est au pouvoir!
On sait à quel point cette quatrième dimension est devenue importante depuis la relativité générale d’Einstein.
Les travaux d’Alicia furent reconnus par la communauté mathématique et elle travailla avec des mathématiciens éminents dont le mathématicien canadien Coxeter considéré comme un des grands géomètres du XXème siècle.
Il faut dire que la fin du XIXe fut fertile pour la géométrie qui, depuis les Grecs, s’était développée sur l’héritage d’Euclide. C’est à cette époque que furent découvertes des géométries non euclidiennes. Par exemple, on découvrit qu’on peut à la fois faire passer une infinité de parallèles (géométrie hyperbolique de Lobatchevski) par un point extérieur à une droite, ou aucune (géométrie elliptique de Riemann). Ce fut l’occasion de polémiques très violentes dans le milieu des mathématiciens.
Mais, comme disait Kipling « C’est une autre histoire! ».
Références
Mary Boole
Frost, Michelle. 1997. Mary Everest Boole. Agnes Scott College. http://www.agnesscott.edu/lriddle/women/boole.htm
Michalowicz, Karen Dee Ann. 1996. « Mary Everest Boole (1832-1916): An Erstwhile Pedagogist for Contemporary Times ». Vita Mathematica: Historical Research and Integration with Teaching, The Mathematical Association of America (éd.), 291–299. Washington D.C. : Ronald Calinger.
Valente, K. G. 2009. « Giving wings to logic: Mary Everest Boole’s propagation and fulfilment of a legacy ». The British Journal for History of Science 43 (1) : 49-74. http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=7332784&fileId=S0007087409990380
Wikipédia. « Manuscrit de Voynich ». https://fr.wikipedia.org/wiki/Manuscrit_de_Voynich, dernière modification le 12 septembre 2019.
Wikipedia. « Mary Everest Boole ». https://en.wikipedia.org/wiki/Mary_Everest_Boole, dernière modification le 29 juillet 2019.
Alicia Boole
Ghys, Etienne. 2015. « Héroïne de la quatrième dimension ». Le Monde. http://www.lemonde.fr/sciences/article/2015/11/09/heroine-de-la-quatrieme-dimension_4805912_1650684.html
Phillips, Tony. « The Princess of Polytopia: Alicia Boole Stott and the 120-cell ». American Mathematical Society. http://www.ams.org/samplings/feature-column/fcarc-boole
Riddle, Larry. 2016. « Alicia Boole Stott ». Agnes Scott College. https://www.agnesscott.edu/lriddle/women/stott.htm
Wikipédia. « Alicia Boole Stott ». https://fr.wikipedia.org/wiki/Alicia_Boole_Stott, dernière modification le 24 mars 2019.
Wikipédia. « Harold Scott MacDonald Coxeter ». https://fr.wikipedia.org/wiki/Harold_Scott_MacDonald_Coxeter, dernière modification le 29 juillet 2019.
Wikipédia. « Hypercube ». https://fr.wikipedia.org/wiki/Hypercube, dernière modification le 4 juillet 2019.

