13 L’analyse spatiale
Un cas d'intervention communautaire de lutte contre le moustique Aedes aegypti au Burkina Faso
Emmanuel Bonnet, Samiratou Ouédraogo et Diane Saré
| Définition de la méthode Méthode d’analyse permettant de mesurer le degré de ressemblance d’un lieu avec ses voisins. |
| Forces de la méthode
Les résultats cartographiques peuvent être expliqués facilement à des décideuses et décideurs et au grand public |
|
Défis de la méthode
|
Les méthodes d’analyse spatiale ont pour objectif de déterminer les caractéristiques de la distribution spatiale des individus géographiques (les ménages par exemple) ou de leurs valeurs (par exemple : le nombre de cas de dengue dans le ménage). Ces caractéristiques peuvent être analysées globalement, c’est-à-dire à une échelle importante comme celle d’une ville entière, pour laquelle les méthodes mettront en évidence le nuage de points des individus géographiques, les relations spatiales entre les valeurs et les individus (dépendance spatiale), et les caractéristiques géométriques (l’organisation des valeurs dans le territoire, comme un gradient nord-sud par exemple) du nuage de points ou des valeurs. Lorsque les valeurs étudiées sont quantitatives, il est possible d’analyser la distribution géographique des valeurs associées aux individus en cherchant notamment s’il existe une relation avec la proximité entre ces individus. L’analyse prend la forme d’un indice qui exprime s’il existe ou non une corrélation entre la valeur des individus et leur proximité. Il permet par exemple de caractériser si les valeurs qui se ressemblent ont tendance à être proches dans le territoire ou, au contraire, sont totalement dispersées. Si les valeurs sont regroupées, on parle alors d’une autocorrélation spatiale positive. Si elles sont dispersées, on parle d’autocorrélation spatiale aléatoire. Cette méthode vise donc à caractériser la dépendance spatiale des valeurs.
De nombreuses situations, en particulier sanitaires, ne sont pas homogènes (on parle aussi de stationnarité). On pense notamment à la concentration de cas de maladie dans des localités très précises, quelques rues d’un quartier par exemple. Imaginons un quartier dont la marge est proche d’une étendue d’eau. Les cas de paludisme existent partout dans celui-ci, mais sont davantage présents et concentrés dans la rue qui borde l’étendue d’eau. La distribution spatiale du paludisme serait dans ce cas hétérogène à l’échelle du quartier. Cependant, les mesures globales de l’autocorrélation spatiale, à l’échelle du quartier dans son ensemble, peuvent occulter ce phénomène de concentration localisé lorsque l’autocorrélation varie d’un lieu à l’autre. L’indice d’autocorrélation spatiale obtenu pourrait signifier que la distribution spatiale des cas de paludisme est homogène dans le quartier, car le calcul, appliqué sur la globalité du territoire, pourrait minimiser la concentration identifiée dans la rue proche du barrage. On dit dans cette situation qu’il existe des associations spatiales de valeurs locales significatives qui ne sont pas détectables par la mesure classique de l’autocorrélation spatiale globale définie par Moran par exemple.
Un des objectifs de l’analyse spatiale est de détecter des formes ou des lieux singuliers où se produisent des concentrations locales de valeurs élevées, appelées aussi agrégats (d’individus ou de valeurs). Des méthodes permettent ainsi une analyse locale très précise et utile pour le ciblage de certaines actions par exemple. Luc Anselin (Anselin, 1995) a développé un indice pour pallier l’effet d’occultation des autocorrélations locales par les indices globaux : les indicateurs locaux d’association spatiale (LISA) (Local indicator of spatial association).
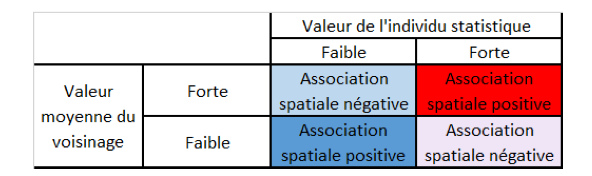
Les LISA permettent de mesurer s’il existe des lieux pour lesquels des valeurs associées aux ménages présentent une relation significative avec la proximité entre ces lieux et s’il existe parmi ces lieux des regroupements de valeurs très élevées ou très faibles. Ces indicateurs mesurent donc la concentration des valeurs numériques mesurées sur un ensemble de points. Le calcul se base sur celui de l’autocorrélation globale de Moran, comme la moyenne des produits des valeurs normalisées des couples de points, pondérées par un poids spatial qui est représenté par la distance. L’analyse LISA s’effectue sur chaque ménage, représenté par un point, et sur les relations de chaque ménage avec ses voisins. Il consiste d’abord à calculer un indice pour chaque point (ménage) à partir de son voisinage. Les indicateurs statistiques expriment le degré de confiance et d’importance que l’on peut accorder aux informations acquises. Dans le cas d’unités spatiales irrégulières pour lesquelles seule la matrice de contigüité est prise en compte, le poids est égal à 1 lorsque les unités sont contiguës et 0 pour les autres. Ainsi, autour du point observé, le LISA local détermine l’étendue d’une région (cluster) formée par des points voisins qui possèdent des valeurs proches de la sienne. La somme des LISA locaux est proportionnelle à l’indicateur global. L’indicateur local se calcul de manière similaire à l’indice de Moran. L’interprétation des LISA obtenus se base sur les hypothèses statistiques de normalité. Il est donc nécessaire de tester la signification statistique des structures en cluster de la région. Une valeur du p est calculée pour chaque point : plus elle faible, plus l’éventuel cluster qu’elle forme avec ses voisins possède une existence statistiquement significative (Caloz et Collet 2011). Il en résulte cinq cas. Le premier, c’est lorsque la valeur p ne permet pas de rejeter l’hypothèse nulle : le point n’est pas considéré comme significatif pour être agrégé avec un autre point. Dans les quatre autres cas, les indices de LISA sont utilisés pour une typologie de quatre agrégats, en fonction de la valeur de l’individu et de la valeur du voisinage. Ces agrégats sont représentés dans le tableau 1, avec la couleur utilisée habituellement pour leur cartographie (Oliveau 2010).
Ce type de méthode est donc adapté, mais rarement utilisé, pour évaluer les effets d’une intervention dans l’espace, à des échelles géographiques très fines comme la localisation des ménages par exemple. Les valeurs analysées à l’échelle des ménages (coordonnées géographiques) peuvent représenter un nombre de personnes atteintes par une maladie par exemple (donnée quantitative). Les LISA seront calculés et représentés cartographiquement avant et après l’intervention afin d’évaluer les effets.
Analyse spatiale des effets d’une intervention communautaire de lutte contre la dengue à Ouagadougou
À la suite à différentes phases d’émergence de la dengue à Ouagadougou au Burkina Faso, il a été décidé de développer et de réaliser une intervention communautaire de lutte contre le moustique Aedes aegypti, principal vecteur de la dengue en milieu urbain.
Site d’étude et participant-e-s
L’étude a été réalisée dans deux quartiers comparables de Ouagadougou (Tampouy et Juvenat), choisis parmi cinq zones identifiées dans la ville. En effet, dans les deux quartiers, il existe des profils socioéconomiques fortement contrastés : des ménages aisés vivant dans des maisons en béton modernes totalement alimentées par les réseaux d’eau et d’électricité, mais aussi des ménages dont le niveau de vie est très bas dans des maisons construites à base d’argile parfois sans commodités de base (Observatoire des populations de Ouagadougou 2013). Ces quartiers sont aussi caractérisés par des zones où la gestion des déchets n’est pas régulièrement assurée et où les détritus s’accumulent dans certaines rues, favorisant ainsi la prolifération des moustiques.

Tampouy, qui se trouve dans la partie nord-ouest de la ville, a été choisie au hasard pour recevoir l’intervention, tandis que Juvenat, du côté est de la ville, a été choisi comme quartier « contrôle », pour en comparer les situations. Dans chaque quartier, nous avons délimité une zone d’un rayon d’un kilomètre autour du centre de santé primaire (considéré comme un point de repère). À Tampouy, l’intervention a été menée dans ce périmètre. Nous avons utilisé les coordonnées géographiques des ménages pour tirer au sort dans ce périmètre (tirage au sort sans remplacement) 287 ménages à Tampouy et 289 ménages à Juvenat, afin de collecter les données entomologiques (larves et nymphes de moustiques) nécessaires à l’évaluation de l’impact de l’intervention.
La théorie de l’intervention
- La mobilisation et l’organisation : cette étape a permis d’établir le contact avec les leaders communautaires et les associations formelles et informelles œuvrant dans la zone de l’intervention à Tampouy pour les informer de la situation de la dengue dans leur quartier. L’étape a favorisé une prise de conscience des personnes influentes de la situation de cette maladie et leur implication dans la lutte.
- La planification opérationnelle : elle consistait en un développement participatif de l’intervention impliquant les personnes influentes et les associations disposées à y participer.
- L’action communautaire : elle consistait en la mise en œuvre des activités de l’intervention par les membres de la communauté (animateurs communautaires et troupe de théâtre) au profit de la communauté. Ces activités visaient à inciter une participation effective des ménages et de la population.
- Le suivi/évaluation mené par la communauté : il a permis une meilleure implication de cette dernière.
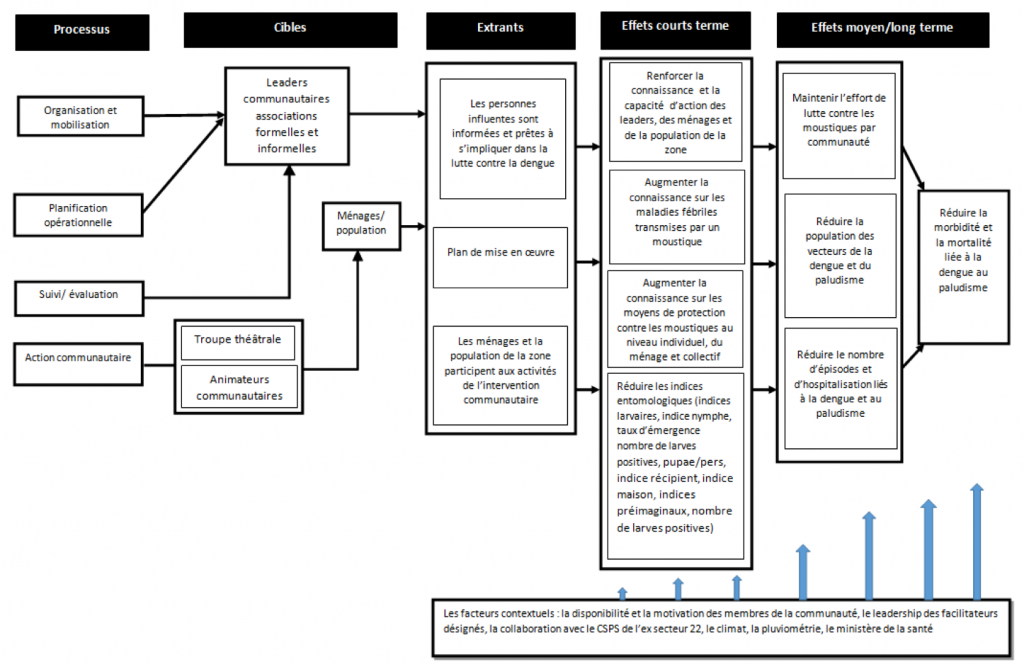
L’interaction de ces différentes composantes a eu pour effets proximaux une augmentation des connaissances sur la dengue et les maladies fébriles à transmission vectorielle, un renforcement de la capacité d’action de la communauté de l’aire de l’intervention, et la réduction des indices entomologiques. Ce chapitre ne vise pas à décrire ces résultats[1].
Les effets distaux attendus sont le maintien de la lutte contre les moustiques, ce qui conduira à une réduction de la population des vecteurs de la dengue et du paludisme et ainsi à une réduction des épisodes et des hospitalisations liées à la dengue et au paludisme.
Devis d’évaluation
Dans le tableau 2, nous résumons le devis d’évaluation de cette intervention dans le contexte spécifique de ce chapitre.
| Objectif d’évaluation | Questions d’évaluation | Planification |
| Évaluer l’impact de l’intervention sur la densité et la distribution géographique des larves et des nymphes d’Aedes aegypti dans le quartier de Tampouy |
Est-ce qu’à la suite de l’intervention le nombre de larves et de nymphes a diminué à Tampouy par rapport à « Juvenat » qui n’a pas reçu d’intervention? Est-ce que suite à l’intervention, des zones de densité de larves et de nymphes persistent à Tampouy par rapport à « Juvenat » qui n’a pas reçu d’intervention? |
Enquêtes entomologiques avant l’intervention, octobre 2015 : les larves et les nymphes d’Aedes aegypti ont été recherchées et collectées par les enquêteurs dans chaque concession visitée des deux quartiers. Juin à début octobre 2016 : réalisation des activités de l’intervention à Tampouy Enquêtes entomologiques après l’intervention fin octobre- début novembre 2016 : les larves et les nymphes d’Aedes aegypti ont été recherchées et collectées par les enquêteurs dans chaque concession visitée dans les deux quartiers. |
Application de la méthode LISA
Les indicateurs locaux d’association spatiale permettent une exploration spatiale locale de l’impact de l’intervention communautaire de lutte contre l’Aedes aegypti au sein du quartier Tampouy de Ouagadougou. À partir des données des enquêtes entomologiques réalisées avant et après l’intervention, la procédure d’analyse se déroule en trois étapes : 1) la cartographie de la distribution spatiale du nombre de larves et de nymphes, 2) la mesure de cette distribution et 3) le calcul des indicateurs locaux d’association spatiale et leur cartographie.
Étape 1 : Analyse de la distribution spatiale du nombre de larves et de nymphes par la cartographie
La première étape est de produire une cartographie des valeurs dans chacun des quartiers avant et après l’intervention en utilisant une échelle de représentation commune. Ces représentations graphiques sont longuement exposées dans plusieurs manuels de cartographie qui permettent pour chaque type de variable et chaque type d’objet géographique (points, lignes, surfaces) de choisir la bonne représentation graphique (Bertin 1967; Bailly 1992).
Plusieurs logiciels, propriétaires (ArcGIs ou Mapinfo) ou libres (QGIs), permettent de réaliser la cartographie du nombre de larves et de nymphes en utilisant une taille de points proportionnels au nombre. Il est nécessaire de disposer des coordonnées géographiques de chaque ménage dans lequel a été réalisée l’enquête entomologique et pour lesquels un nombre total de larves et de nymphes a été calculé. À ce titre, pour éviter les biais d’interprétation, un plan de sondage spatial (tirage aléatoire dans l’espace) pour la collecte entomologique est nécessaire.
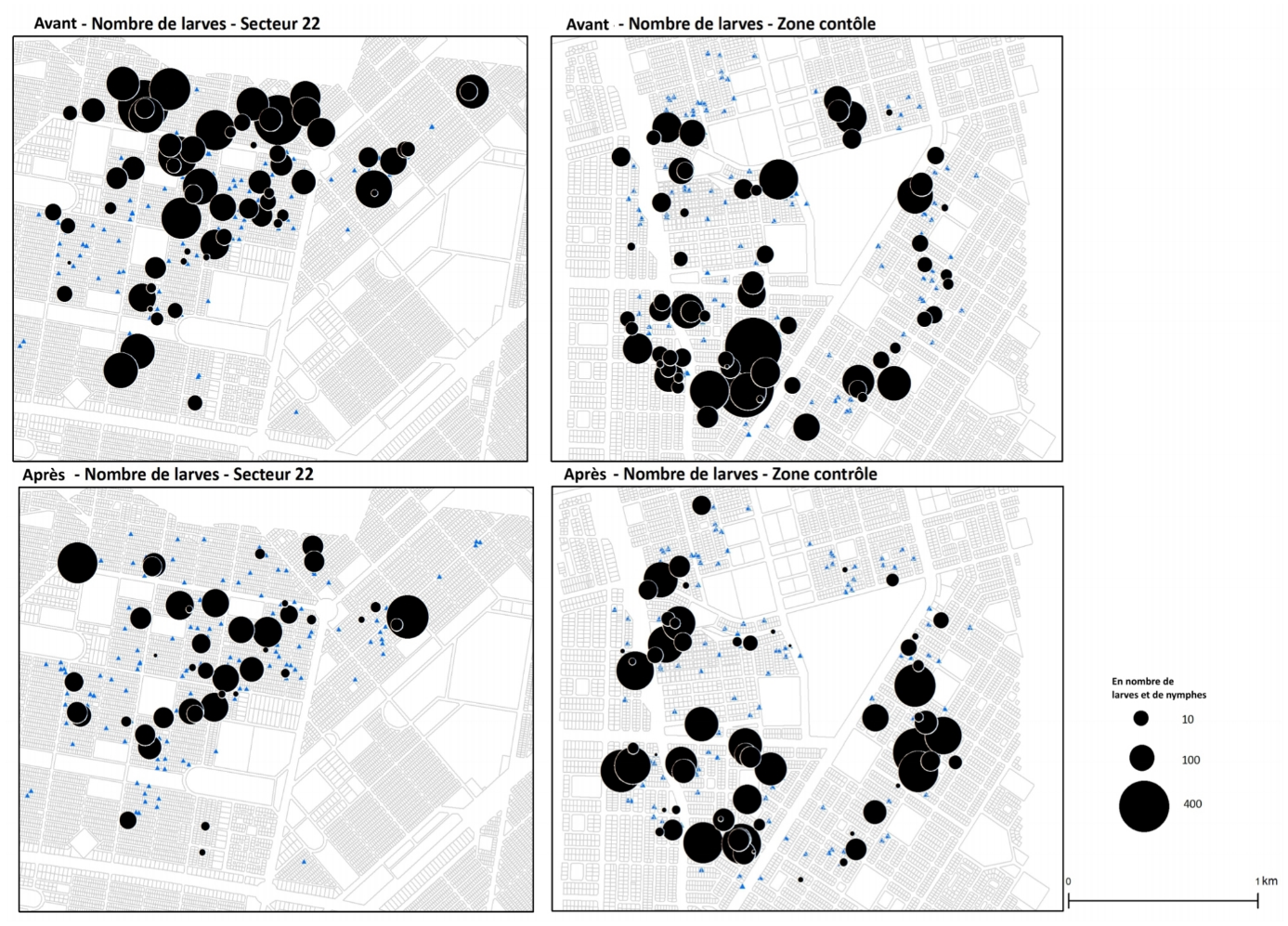
Les cartes (figure 1) représentent tous les ménages où les données ont été collectées. Si aucune larve n’a été relevée, le ménage est représenté par un point bleu sur la carte, il n’exprime aucune quantité. Pour les autres ménages, le point noir représenté est graphiquement proportionnel au nombre de larves et de nymphes calculé. La comparaison des cartes permet d’observer plusieurs phénomènes.

Lors de la phase initiale, avant l’intervention, on observe un nombre de larves et de nymphes important dans la zone d’intervention et la zone contrôle. Dans chacune d’elles, des zones apparaissent avec un nombre de larves et de nymphes plus important que dans d’autres parties des quartiers. Cela illustre que les larves d’Aedes aegypti sont présentes partout à Ouagadougou et qu’il existe, pour des raisons multiples, des « poches » dans lesquelles ces larves sont plus nombreuses.
Lors de l’enquête finale après l’intervention, on observe une diminution importante du nombre de ménages avec des gîtes larvaires et de nymphes à Tampouy, le secteur d’intervention. Dans le secteur contrôle, Juvenat, qui n’a pas reçu d’intervention, on observe que les gîtes identifiés lors de la phase initiale sont majoritairement présents, et l’apparition de nouveaux gîtes. Notons que les effets ne sont pas associés à une pluviométrie plus faible dans une zone par rapport à une autre, et d’une année à l’autre, et donc d’une plus faible productivité de gîtes larvaires.
Cette première étape est simple à réaliser, elle apporte une représentation cartographique du phénomène. Cependant, pour caractériser les « poches » et mesurer s’il existe une concentration du nombre de gîte et de larves dans certaines parties des quartiers et comment elle a évolué après l’intervention, il faut réaliser des mesures globales puis locales des valeurs associées aux ménages.
Étape 2 : Mesure de la distribution spatiale du nombre de larves et de nymphes au sein des quartiers de l’étude à Ouagadougou
Pour cette étape, on mesure l’autocorrélation spatiale pour déterminer s’il existe une corrélation entre la valeur des objets et les relations métriques ou topologiques entre ces objets. Pour rendre compte des valeurs voisines, on utilise des indices de corrélation, dont l’indice de Moran, le plus utilisé. Il se définit comme la moyenne des produits des valeurs normalisées des couples de points, pondérée par la distance entre les deux points (Moran, 1948).

Cet indice mesure donc à quel point, pour l’ensemble de l’échantillon, la valeur des individus est proche ou éloignée de celle de leur voisinage par rapport à celle de la moyenne. Cette mesure est globale (Cliff, 1969) puisqu’elle porte sur la similarité des lieux avec leur voisinage pour l’ensemble de l’échantillon. Dans le cas de cette évaluation, l’indice de Moran indique si les habitations des ménages avec un nombre de larves et de nymphes important sont proches ou éloignées, révélant ainsi une autocorrélation spatiale positive ou négative. C’est la première étape avant de chercher à approfondir la localisation d’agrégats.
La valeur de l’indice de Moran dans le quartier de Tampouy avant l’intervention montre une autocorrélation spatiale positive (si l’indice est supérieur à zéro), relativement faible (i=0,10), mais avec une dispersion des valeurs de l’indice qui suggère que des agrégats sont possiblement présents. Après l’intervention, on remarque que l’autocorrélation spatiale est nulle (i=-0,02) ce qui signifie que les valeurs sont distribuées de manière aléatoire, sans autocorrélation, et démontre une évolution entre les deux phases de collecte et donc un effet de l’intervention. Dans le secteur contrôle, l’autocorrélation spatiale globale est également positive (i=0,05) avant l’intervention et nulle (i=-0,004) après. L’évolution globale dans les deux quartiers est donc similaire. Cependant, il est important de vérifier l’évolution au niveau local, c’est-à-dire au niveau de l’habitation des ménages, pour notamment vérifier s’il existe des agrégats, et si oui, comment ils ont évolué.
Étape 3 : Indicateurs locaux d’association spatiale du nombre de larves et de nymphes au sein des quartiers
Les indicateurs locaux d’association spatiale développés par Luc Anselin permettent de réaliser ces évaluations. Ils analysent la concentration des valeurs similaires et dissimilaires mesurées sur un ensemble de points ou calculées par agrégation spatiale.
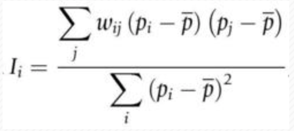
où pi et pj sont les valeurs des unités spatiales i et j telles que i et j sont considérées comme voisines compte tenu de la mesure de leur degré de voisinage, pi est la valeur moyenne des unités spatiales et wij une mesure de la proximité des unités spatiales i et j.
La procédure peut se réaliser avec le logiciel libre Geoda (Anselin, 1995). Il permet la réalisation de toutes les étapes précédentes et ne nécessite pas le recours à un système d’informations géographiques pour préparer les données à utiliser. En revanche, les résultats sont exportables vers les SIG. Avant de faire l’analyse des indicateurs locaux d’association spatiale, il faut définir une matrice de poids (tableau qui recense toutes les distances entre tous les voisins) qui identifie les voisins. Les poids des voisins peuvent être construits de plusieurs manières en fonction du type d’objet géographique (un point ou une surface). Dans le cas de l’intervention de lutte contre la dengue présentée ici, les ménages sont représentés par des points. La matrice est donc calculée à partir d’une distance entre les points.
La dernière étape consiste à lancer l’analyse de LISA à partir de cette matrice de poids. Une statistique est calculée pour chaque unité, elle est basée sur la valeur des unités voisines. Il résulte deux types de cartes : une qui représente les valeurs de l’indice calculé et qui permet de visualiser comment l’indice varie dans le territoire, et une autre qui permet de mettre en évidence les relations statistiquement significatives des indices par une cartographie des agrégats qui illustre les similarités et dissimilarités de valeurs.
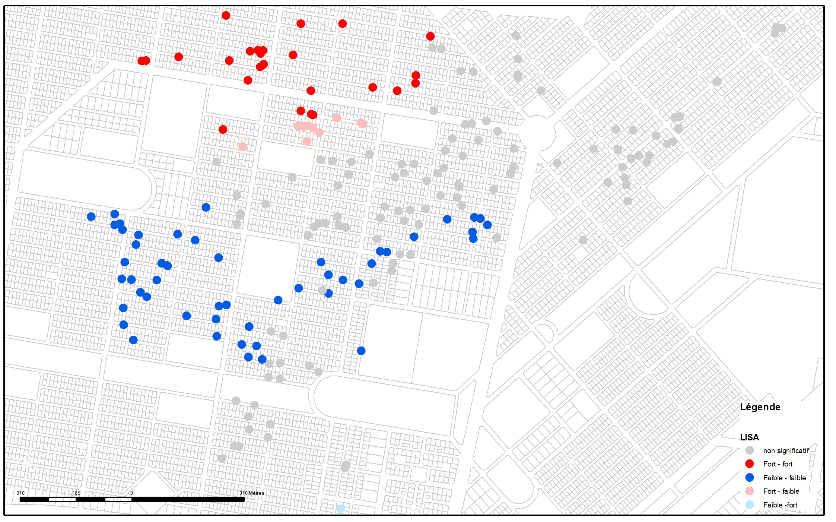
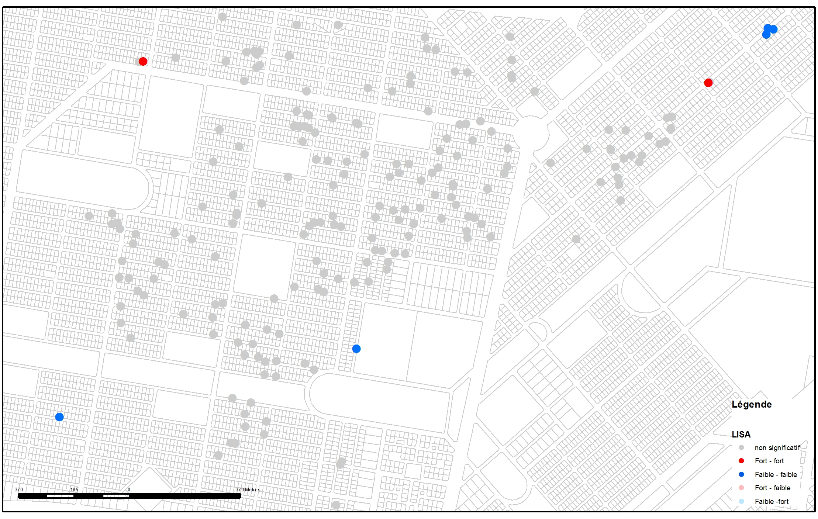
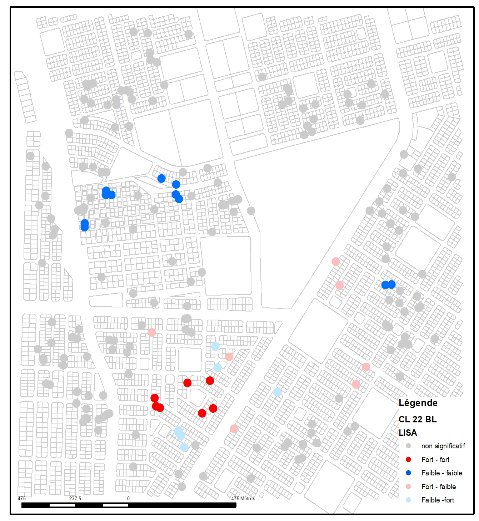
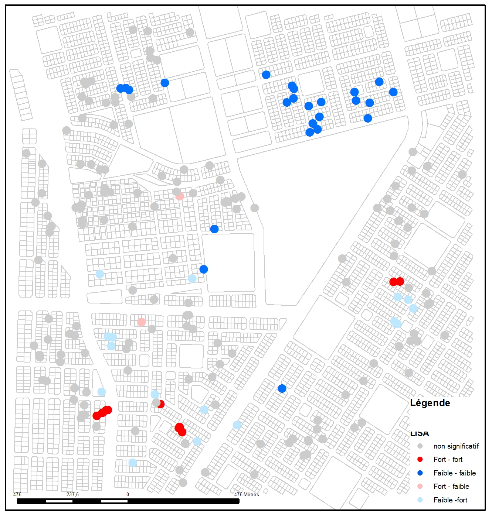
Les cartes LISA (figures 3a, 3b, 3c et 3d) des valeurs de larves et de nymphes réalisées pour le quartier d’intervention Tampouy (en haut) montrent qu’avant l’intervention, des agrégats de valeurs négatives (en bleu) et de valeurs positives (en rouge) étaient présents. Cela signifie qu’il existait des concentrations de deux types, très tranchées dans le quartier. En bleu, on voit une concentration de ménages qui avaient des gîtes larvaires et de nymphes relativement peu productifs, car ils avaient un faible nombre de larves et de nymphes. Cette concentration de valeurs en faible-faible signifie également que les ménages voisins avaient des caractéristiques similaires (faible nombre de larves). À l’inverse, au nord de la zone, la concentration de valeurs fortes est représentée par les points classés en forte-forte (valeurs fortes du ménage et de ses voisins). L’analyse LISA met donc en évidence une double concentration de valeurs de larves et de nymphes opposées. Cela ne signifie pas une présence ou une absence de larves et de nymphes, mais qu’il y avait des zones graduées de productions de larves et de nymphes dans l’aire étudiée avant l’intervention.
Après l’intervention, on constate que les analyses LISA révèlent peu d’agrégats de tous types et la disparation d’agrégats qui existaient avant l’intervention. L’analyse met donc en évidence que l’intervention a permis la réduction du nombre de zones de concentration de valeurs fortes et faibles de larves et de nymphes. L’analyse globale le confirme avec une autocorrélation spatiale nulle qui signifie que la présence de larves et de nymphes sur la zone d’intervention est désormais aléatoire. Cette analyse complète les analyses des épidémiologistes qui ont observé une réduction importante des indices entomologiques à Tampouy après l’intervention.
Dans la zone contrôle, on observe des agrégats qui persistent dans les mêmes lieux lors de la collecte après l’intervention et confirment l’augmentation de la production de larves et de nymphes identifiée par les autres analyses épidémiologiques.
Analyse réflexive et conclusion
L’évaluation de la dimension spatiale dans les interventions en santé publique est souvent limitée à une analyse des effets moyens de l’intervention qui varient en fonction des entités géographiques et des mesures approximatives de la distance. Les méthodes traditionnelles utilisées pour l’évaluation ne permettent pas de rendre compte de la variabilité spatiale des lieux et des effets des interventions. La méthode utilisée dans ce chapitre est un exemple d’analyse spatiale qu’il est possible d’utiliser. Ces méthodes sont rarement mobilisées pour l’évaluation des interventions et davantage pour explorer la diffusion ou la concentration d’une maladie dans l’espace. Or, cet exemple démontre que les phénomènes peuvent être observés à différentes échelles et que les résultats globaux peuvent cacher des situations locales différentes. Ces analyses viennent compléter, par leur dimension spatiale, les autres résultats dans le cadre de l’évaluation d’impact d’une intervention. Généraliser l’utilisation des analyses spatiales dans l’évaluation des interventions est donc à recommander pour appréhender tous les effets à toutes les échelles.
Dans l’exemple présenté, la procédure utilisée s’est avérée efficace et n’a pas posé de difficultés dans la mesure où l’échantillonnage était géographique. C’est un des points fondamentaux des méthodes d’analyse spatiale. La qualité des résultats dépend d’un plan d’échantillonnage géographique pour assurer une interprétation correcte des résultats. L’un des enjeux de cette méthode est de retrouver les ménages lors de la phase post-intervention. Dans les pays où l’adressage des rues est inexistant, il faut avoir recours à des GPS et s’assurer que la géolocalisation est correcte et bien enregistrée. Dans les milieux urbains denses, certaines perturbations du signal brouillent les positions enregistrées dans les GPS et complexifient la possibilité de retrouver les ménages enquêtés en phase de pré-intervention. Lors de l’enquête auprès des populations il faut s’assurer d’enregistrer le numéro de téléphone de la personne enquêtée afin de servir d’alternative pour retrouver le ménage. Ne pas retrouver le ménage de l’enquête initiale est la principale faiblesse de la méthode sur le plan de sa mise en œuvre dans les pays à plus bas revenu. Les autres faiblesses sont relatives à la méthode en elle-même qui ne permet d’analyser qu’une variable à la fois, limitant ainsi la prise en compte d’autres variables pouvant être considérées comme des facteurs de confusion. Toutefois, il existe d’autres méthodes géographiques qui combinent plusieurs variables et seraient complémentaires (régressions géographiquement pondérées GWR) aux évaluations statistiques.
L’accès à ces méthodes est aujourd’hui facilité par la disponibilité de logiciels de Systèmes d’Informations Géographiques libres comme QGIS. Ils permettent de cartographier la géolocalisation des ménages d’une enquête, mais aussi de réaliser un échantillonnage géographique. Associés aux outils libres « GéoDa » développés par Luc Anselin, la réalisation des LISA est également facilitée.
Références
Anselin, L., (1995). Local indicators of spatial association – LISA. Geographical Analysis, 27(2), 93-115.
Bailly A. S. (1999). Pumain D. et Saint-Julien T., L’analyse spatiale T. 1. Annales de Géographie, (605), 105.
Bertin, J. (1967). La sémiologie graphique : les diagrammes, les réseaux, les cartes. La Haye ou Paris : Mouton ou Gauthier-Villars.
Caloz, R. et Collet, C. (2011). Analyse spatiale de l’information géographique (1e éd.). Lausanne : Presses polytechniques et universitaires romandes
Cliff, A. D. et Ord, K. J. (1969). The problem of spatial autocorrelation. Dans A. J. Scott (dir.), Papers in Regional Science, Studies in Regional Science (vol. 1, p. 25-55). Londres: Pion.
Moran, P. A. (1948). The interpretation of statistical maps. Journal of the Royal Statistical Society: Series B, 10(2), 243-251.
Observatoire des populations de Ouagadougou, Projet Wellcome Trust 2008-2013. (2013). Rapport scientifique sur la caractérisation sociologique des quartiers de l’OPO. Repéré à http://www.issp02.issp.bf/opo/Publications/Rapport-scientifique-juin2013-Caracterisation-des-quartiers-Axe-qualite.pdf
Oliveau, S. (2010). Autocorrélation spatiale : leçons du changement d’échelle. L’Espace Géographique, 39(1), 51-64.
Résumé / Abstract / Resumen
Ce chapitre présente une analyse spatiale d’une intervention qui vise à évaluer si des valeurs similaires d’un résultat sont plus susceptibles de former des grappes dans une zone d’étude. Cette méthode appelée « indicateurs locaux d’association spatiale » (local indicators of spatial association – LISA) permet d’identifier les zones où les valeurs sont spatialement dépendantes les unes des autres. LISA a été utilisé pour évaluer l’effet d’une intervention communautaire visant à contrôler le moustique responsable de la propagation de la dengue Aedes aegypti dans deux quartiers de Ouagadougou, capitale du Burkina Faso. L’évaluation finale de l’intervention à l’aide de cette méthode a montré que les groupes de larves ont disparu dans le quartier qui a reçu l’intervention alors qu’ils persistaient dans le quartier témoin.
***
This chapter present a spatial analysis of an intervention which aims at assessing whether similar values of an outcome are more likely to form clusters in a study area. This method called local indicators of spatial association (LISA) enable to identify areas where values are spatialy dependant with one another. LISA has been used to evaluate the effect of a community-based intervention which aims at controlling the mosquito responsable for spreading Dengue, Aedes aegypti in two neighborhoods of Ouagadougou the capital city of Burkina Faso. The final evalutation of the intervention using this method showed that larva clusters disappeared in the neighborhood which received the intervention while they persisted in the control neighborhood.
***
Este capítulo presenta un análisis espacial de una intervención para evaluar si los valores similares de un resultado tienen más probabilidades de formar grupos en un área de estudio. Este método, denominado « indicadores locales de asociación espacial » (LISA), identifica áreas en las que los valores dependen espacialmente unos de otros. LISA se utilizó para evaluar el impacto de una intervención comunitaria para controlar al mosquito responsable de la propagación del dengue Aedes aegypti en dos barrios de Uagadugú, la capital de Burkina Faso. La evaluación final de la intervención utilizando este método mostró que los grupos de larvas desaparecieron en el área que recibió la intervención mientras persistían en el área de control.
***
Emmanuel Bonnet est géographe de la santé et chargé de recherches à l’IRD (Institut de Recherche pour le Développement). Il a mené de nombreuses recherches en Afrique de l’Ouest et possède une expérience internationale dans les domaines de la surveillance des épidémies, des technologies géomatiques, des systèmes d’informations géographiques et de l’analyse spatiale.
Samiratou Ouédraogo est épidémiologiste et chercheure en santé publique avec une expérience internationale en évaluation. Elle travaille sur de nombreux projets de recherche au Canada et en Afrique.
Diane Saré est médecin de santé publique. Elle possède une expérience professionnelle clinique tant en milieu communautaire qu’en milieu hospitalier. Elle possède également une expérience en mise en œuvre et en évaluation d’intervention communautaire.
Citation
Emmanuel Bonnet, Samiratou Ouédraogo et Diane Saré. (2019). L’analyse spatiale. Un cas d’intervention communautaire de lutte contre le moustique Aedes aegypti au Burkina Faso. In Évaluation des interventions de santé mondiale. Méthodes avancées. Sous la direction de Valéry Ridde et Christian Dagenais, pp. 333-351. Québec : Éditions science et bien commun et Marseille : IRD Éditions.
- Pour plus d'information, voir le site http://www.equitesante.org/dengue-interventions-communautaires/ ↵

