9 Les méthodes quasi-expérimentales
L’effet de l’âge légal minimum sur la consommation d’alcool chez les jeunes aux États-Unis
Tarik Benmarhnia et Daniel Fuller
| Définition de la méthode Le terme « quasi-expérimental » fait référence à une « expérimentation avec une intervention donnée, des résultats de santé mesurés et au moins deux unités expérimentales (groupe recevant l’intervention et groupe contrôle), mais sans recours à la randomisation pour créer les conditions d’inférence causale » (Cook, Campbell et al. 1979) |
| Forces de la méthode
Les méthodes quasi-expérimentales constituent un excellent devis d’étude alternatif aux essais contrôlés randomisés lorsque ces derniers sont difficiles ou impossibles à mener. En effet, ces méthodes permettent, en se basant sur des situations observées où il n’y a pas eu de répartition délibérée et aléatoire des groupes d’intervention et de contrôle, de se baser également sur la notion de contrefactuel pour estimer des effets de nature causale |
| Défis de la méthode
Chaque méthode quasi-expérimentale nécessite de respecter des hypothèses de travail supplémentaires. Parfois ces hypothèses sont impossibles à vérifier empiriquement. Les effets qui sont estimés peuvent varier en ce qui concerne les populations concernées et tout comme pour les essais contrôlés randomisés, il est important de distinguer validité interne et validité externe. |
L’évaluation des effets des politiques publiques sur la santé des populations est un domaine qui s’est particulièrement développé dans les dernières années. L’évaluation des effets se distingue d’autres types d’évaluations telles que l’évaluation d’implantation (Sabatier et Mazmanian 1980; Belaid et Ridde 2012) ou l’évaluation économique (Brousselle et Lessard 2011; Drummond, Sculpher et al. 2015, Brousselle, Benmarhnia et al. 2016). Évaluer les effets des politiques publiques sur la santé des populations est essentiel pour plusieurs raisons (Champagne, Contandriopoulos et al. 2009; Macintyre 2010). Cela permet i) de s’assurer que ces politiques contribuent à améliorer l’état de santé de la population, ce qui constitue un des mandats de la santé publique, ii) de s’assurer que des objectifs d’un programme de santé publique sont bel et bien atteints, iii) d’expérimenter de nouvelles interventions et de décider quant au maintien, à la modification ou à l’arrêt d’interventions existantes et iv) de s’assurer que les ressources publiques sont utilisées de manière efficace. Dit simplement, l’objectif principal de ce type d’évaluation est d’attribuer des changements à une intervention en particulier quant à un indicateur de santé spécifique. Autrement dit, il est question d’attribuer un effet causal à une intervention sur un indicateur de santé dans un contexte particulier.
La notion d’inférence causale est centrale dans de nombreuses disciplines aujourd’hui, incluant l’économétrie, la psychologie sociale ou l’épidémiologie. L’un des modèles les plus souvent utilisés pour identifier des effets de nature causale est basé sur la notion de contrefactuel (Susser 2001; Pearl 2009; Naimi et Kaufman 2015). Par exemple, pour évaluer si des changements de résultats de santé sont directement attribuables à une intervention, on cherchera à les comparer au sein d’un groupe observé (que l’on appellera factuel) à un groupe hypothétique semblable ou interchangeable (que l’on appellera contre-factuel) qui ne se distingue que par une seule caractéristique, à savoir le fait de ne pas avoir reçu l’intervention. Ainsi, on mesurera l’effet causal par le contraste entre le groupe factuel et le groupe contre-factuel. Le Problème fondamental de la causalité (Holland 1986; Kaufman 2007) est que, par définition, ce groupe contre-factuel n’est pas directement observable. Ainsi, la randomisation a été proposée comme solution pour pallier ce problème, tout en permettant de maintenir l’interchangeabilité et la substitution entre les groupes exposés à l’intervention ou non, et permettant de s’assurer de ne pas enfreindre des hypothèses permettant l’inférence causale, de façon à ce que l’intervention ne puisse avoir un effet sur les résultats de santé que du groupe factuel uniquement, par exemple. La randomisation permet notamment de pallier l’enjeu capital qu’est la prise en compte des facteurs de confusion mesurés ou non (Bonell, Hargreaves et al. 2011). C’est ainsi que les essais contrôlés randomisés (ECR) ont été introduits et utilisés en médecine et en sciences sociales : un groupe est assigné aléatoirement à l’intervention (ou au traitement) et un groupe ne l’est pas. Cette répartition aléatoire permet ainsi de s’assurer qu’il n’y a pas de différence entre les deux groupes avant l’intervention, autrement dit qu’il n’y a pas de biais de confusion, mesurés ou non. Cependant, ce type d’expérimentation, où l’on choisit délibérément d’intervenir sur un groupe et non sur un autre (le groupe contrôle) n’est pas faisable dans de nombreuses situations, que ce soit pour des raisons de coût ou des raisons éthiques (Royall 1991; Hawe, Shiell et al. 2004; Moore et Moore 2011; Petticrew, Chalabi et al. 2011).
Les « expérimentations naturelles » constituent un excellent devis d’étude alternatif aux ECR, car elles permettent, en se basant sur des situations observées et sans répartition délibérée et aléatoire des groupes d’intervention et de contrôle, de se baser également sur la notion de contre-factuel pour estimer des effets de nature causale (Bor 2016). Pour cela, les méthodes quasi-expérimentales (MQE) ont été développées pour concevoir des groupes contre-factuels en se basant uniquement sur des données observées. Le terme de « quasi-expérimental » fait référence à une « expérimentation avec une intervention donnée, des résultats de santé mesurés et deux unités expérimentales (groupe recevant l’intervention et groupe contrôle), mais sans recours à la randomisation pour créer les conditions d’inférence causale » (Cook, Campbell et al. 1979 : 14); Shadish et Cook 2009). Ainsi, les MQE permettent d’imiter les résultats que produirait un ECR, tout en ne servant que de situations existantes. Plusieurs MQE ont été développées pour évaluer les effets des politiques publiques et commencent à être utilisées en santé publique.
Périmètre du chapitre
Ce chapitre vise à présenter deux principales méthodes quasi-expérimentales (MQE) et leur application dans une étude qui vise à évaluer l’effet de l’âge légal minimum sur la consommation d’alcool chez les jeunes. Ces MQE permettent de prendre en compte les facteurs de confusion non mesurés qui peuvent avoir un impact important sur la validité des estimations. Des méthodes qui permettent de prendre en compte uniquement les facteurs de confusion mesurés, comme des méthodes d’appariement utilisant un score de propension par exemple, sont parfois décrites comme MQE (Shadish, Luellen et al. 2006; Austin 2011). Cependant, dans ce chapitre, nous ne les aborderons pas. Nous nous focaliserons plutôt sur deux types de MQE : la méthode de « différence dans les différences » (DD), ainsi qu’un type particulier de variable instrumentale, à savoir l’approche de « régression avec discontinuité » (RD).
Les variables instrumentales pour évaluer l’effet des politiques publiques sont couramment utilisées en économétrie (Newhouse et McClellan 1998; Hernán et Robins 2006) où, par ailleurs, une terminologie distincte est utilisée. Dit simplement, une variable instrumentale est une variable qui sera fortement corrélée à la probabilité de bénéficier d’une intervention, mais qui ne sera aucunement liée à l’issue de santé d’intérêt. Ainsi, on pourra utiliser cette variable instrumentale pour pallier les potentiels biais de confusions (mesurés ou non) dans la relation entre la probabilité de bénéficier de l’intervention et d’éventuels changements de l’issue de santé d’intérêt (voir Angrist et Pischke 2008 et 2014). Des variables géographiques (frontières, altitude, pluviométrie…) ou génétiques pourront notamment être utilisées comme variables instrumentales. Nous n’aborderons pas le cas général des variables instrumentales dans ce chapitre. De même, nous n’aborderons pas les analyses de séries temporelles interrompues comme MQE pour évaluer les effets des politiques publiques (voir Fuller, Sahlqvist et al. 2012; Benmarhnia, Zunzunegui et al. 2014; Kontopantelis, Doran et al. 2015).
L’objectif général de ce chapitre est de décrire deux MQE, de les appliquer empiriquement à un exemple basé sur une simulation et de fournir tous les éléments, incluant les hypothèses préalables à vérifier, les différentes étapes à mener et la syntaxe pour mener les analyses avec les logiciels R et Stata. Ceci permettra aux lecteurs et lectrices de reproduire ce type d’analyses dans leur contexte d’évaluation.
Il est possible de retrouver en ligne toutes ces ressources informatiques, ainsi que toute la syntaxe permettant de les appliquer à d’autres questions de recherche, à l’adresse https://github.com/walkabilly/methode_evaluation. Il faut en profiter!
Présentation du contexte d’évaluation : les interventions pour réduire la consommation d’alcool chez les jeunes
Dans ce chapitre, nous prendrons comme exemple de politique publique le changement de l’âge légal minimum pour consommer de l’alcool afin de réduire la consommation chez les jeunes.
La consommation d’alcool est un contributeur important au fardeau de morbidité et mortalité chez les adolescent-e-s et jeunes adultes dans de nombreux pays (Rehm, Gmel et al. 2003). Il existe de nombreuses interventions visant à prévenir la consommation d’alcool chez les jeunes. Depuis de nombreuses décennies, plusieurs pays ont mis en place un âge légal minimum pour la consommation d’alcool (Carpenter et Dobkin 2011). Malgré ce cadre légal et de nombreuses autres interventions de santé publique visant à réduire la consommation d’alcool chez les jeunes, l’alcool continue d’être un contributeur important à la mortalité. Ainsi, plusieurs pays ont décidé d’augmenter cet âge légal de consommation d’alcool avec pour objectif de réduire la consommation d’alcool et prévenir les accidents attribuables à la consommation. Quelques études ayant évalué ce type de politique publique avec des MQE de type DD ou RD ont été publiées ces dernières années (Donald et Lang 2007; Carpenter et Dobkin 2009; Yörük et Yörük 2012). Ici, en nous basant sur des données simulées, nous présenterons comment appliquer deux approches permettant d’estimer les effets de ce type de politique publique sur la consommation d’alcool chez les jeunes.
Présentation et application des méthodes proposées
Méthode de « différence dans les différences »
Présentation générale de la méthode DD
La méthode dite de différence dans les différences (DD) se sert d’un ou plusieurs groupes contrôle pour approximer la trajectoire d’un groupe contre-factuel n’ayant pas reçu d’intervention qui serait interchangeable avec le groupe ayant reçu l’intervention. Par exemple, ce ou ces groupe(s) contrôle pourront être des pays ou régions n’ayant jamais reçu ce type d’intervention ou l’ayant reçu à un moment différent du groupe d’intervention considéré. L’hypothèse principale à considérer dans ce type d’approche est qu’en l’absence de l’intervention, les tendances du groupe contrôle sont une bonne approximation des tendances du groupe qui recevra l’intervention (Angrist et Pischke 2008; Dimick et Ryan 2014). Autrement dit, si l’intervention n’avait pas eu lieu, les tendances entre les deux groupes vis-à-vis de l’indicateur d’intérêt resteraient constantes.
Considérons schématiquement deux États dans le même pays, à quatre temps d’observation (2009 [t0], 2010 [t1], 2011 [t2], 2012 [t3]), un État implantant l’intervention en 2010 (t1) et l’autre État ne faisant rien. En assumant et/ou en vérifiant que les deux États sont interchangeables, on commencera par estimer la première différence qui sera par exemple, la différence de prévalence de consommation d’alcool chez les jeunes entre les deux États à toutes les périodes de temps confondues. Ensuite on estimera cette même différence en contrôlant l’effet du temps et de l’État. L’hypothèse nulle (l’intervention n’a pas d’effet sur la consommation d’alcool chez les jeunes) impliquerait que ces deux différences demeurent égales dans le temps. Ainsi, si les deux États sont interchangeables et que l’hypothèse de DD est respectée, alors toute différence entre ces deux différences pourra être interprétée comme l’effet de l’intervention sur la consommation d’alcool chez les jeunes dans l’État ayant reçu l’intervention.
Description des données
L’objectif de cette étude est d’estimer l’impact sur la consommation d’alcool d’une politique publique organisée en 2011 et ayant augmenté l’âge légal pour la consommation d’alcool de 18 à 19 ans dans 10 États du pays.
Afin de présenter l’application de la méthode de différences dans les différences, nous avons créé une base de données simulée qui contient des données semblables à un recensement national. Nous présumons 20 000 répondants âgés de 16 à 25 ans échantillonnés dans 20 États. La probabilité de sélection chez les répondant-e-s est égale pour chaque État. Nous présumons une probabilité égale de sélection pour éviter le besoin de pondération. Cependant, il est tout à fait possible d’inclure les pondérations dans l’application de cette méthode.
Le recensement contient les variables suivantes :
- étatID : l’identificateur unique pour les États.
- individuID : l’identificateur unique pour les répondant-e-s.
- connaissance : une variable individuelle de connaissance au sujet de l’alcool. Une augmentation de la valeur indique une connaissance plus importante au sujet de l’impact négatif de l’alcool.
- effetTemps : indique l’année avec des valeurs entre 2009 et 2012 inclusivement.
- loi : variable binaire qui indique si l’état a adopté ou non la loi augmentant l’âge de consommation de 18 à 19 ans (c’est-à-dire la politique publique).
- âge : une variable qui indique l’âge du répondant ou de la répondante.
- consParSem : nombre de consommation d’alcool par semaine du répondant ou de la répondante.
Ainsi, nous avons les données nécessaires pour faire une analyse de différences dans les différences. La base de données simulée présentée ici est typique pour une analyse de DD. Celle-ci inclut des données sur plusieurs années (deux au minimum), différents États, une politique implantée de manière différentielle à différentes années entre les États. Ces conditions sont nécessaires afin de construire le contre-factuel et mener l’analyse de DD.
Construire un contre-factuel
Le contre-factuel est représenté par une condition inobservable où la politique publique n’est pas implantée. Dans le cas où le contre-factuel est valide, nous ne présumons aucune modification de la consommation d’alcool dans les États où la politique n’a pas été implantée, donc pas d’effet de la politique publique. Nous avons inclus les ajustements par temps, État, âge et connaissances des effets négatifs de l’alcool sur la santé, afin de créer le contrefactuel le plus plausible possible. Afin que l’hypothèse principale de la méthode DD soit validée, nous devons aussi présumer que la pente de consommation par semaine dans le temps suit la même trajectoire dans les États d’intervention et de contrôle (voir Figure 1).
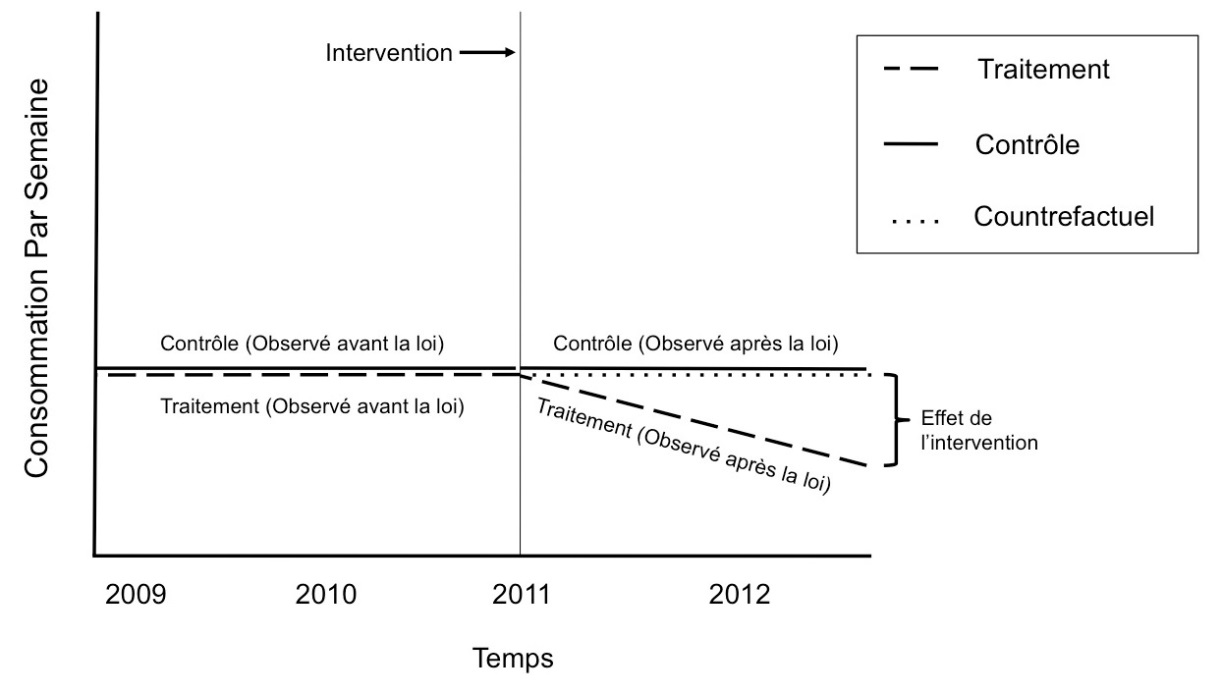
Estimer l’effet de la politique publique
Avant de poursuivre l’estimation de l’effet de la politique publique, les procédures standard de nettoyage de données sont requises. Nos données simulées ne contiennent ni données manquantes ni données aberrantes. Étant donnée la distribution de notre variable d’intérêt (nombre de consommation d’alcool par semaine), nous allons utiliser un modèle de type binomial négatif (pour plus de détails, voir Hilbe 2011).
Afin d’estimer l’effet de la loi sur la consommation d’alcool en utilisant la méthode de DD, nous allons procéder en quatre étapes.
Étape 1 : La première étape consiste à inclure la variable d’intervention (loi) qui indique si un État a adopté ou non la loi augmentant l’âge de consommation d’alcool de 18 et 19 ans. Le Modèle 1 (Tableau 1) présente le résultat de l’inclusion de variable loi dans le modèle. L’effet de la loi est une réduction d’environ une unité de consommation d’alcool par personne chez les 16-25 ans (Beta : -1,11, IC 95 % -1.08 à -1,13). La variable loi est une comparaison brute entre le groupe traitement et le groupe contrôle, celle-ci ne contrôle pas deux facteurs importants, soit l’effet du temps et les différences entre les États.
Étape 2 : Le Modèle 2 (Tableau 1) ajoute un effet fixe pour la variable temps. Pour cela, nous avons inclus une variable catégorielle pour chaque année. L’inclusion de cette variable contrôle l’effet séculaire de la consommation d’alcool dans le temps, ceci sans contrainte linéaire sur l’effet du temps. L’effet estimé pour la variable loi sur notre variable d’intérêt reste semblable à l’étape précédente avec une réduction d’environ une unité de consommation d’alcool par personnes chez les 16-25 ans (Beta : -1,08, IC 95 % -1.08 à -1,03).
Étape 3 : Le Modèle 3 (Tableau 1) ajoute un effet fixe pour les États. Nous avons inclus une variable catégorielle pour chaque État. L’inclusion de cette variable permet de contrôler pour toute caractéristique spécifique au niveau de l’État observable et non observable qui est invariant dans le temps. L’inclusion des effets fixes pour le temps (cf. étape 2) et l’État nous permet d’estimer l’effet intra-État avant et après la loi entre les États avec traitement, ceux qui organisent la loi, et les États contrôle, ceux qui ne l’organisent pas. Dans le Modèle 3, l’effet estimé pour la variable loi sur notre variable d’intérêt reste statistiquement significatif, mais l’ampleur de l’association est réduite (-0,32, IC 95 % -0.39 à -0,24).
Étape 4 : Dans le Modèle 4 (Tableau 1), nous ajoutons les deux variables individuelles, le niveau de connaissance et l’âge des individus. L’inclusion de ces variables ne change pas notre estimation de l’effet de la loi sur la consommation (-0,32, IC 95 % -0.39 à -0,24).
Conclusion
Nous avons pu estimer, en utilisant la méthode de DD, l’effet d’une politique publique visant à changer l’âge légal sur la consommation d’alcool chez les 16-25 ans. Nous avons trouvé que cette politique publique contribuait à réduire la consommation d’alcool dans le groupe d’âge visé.
Ainsi, en utilisant les contrastes entre les États quant à la date d’implantation de cette politique publique, nous avons pu construire des contre-factuels qui nous ont permis de comparer les changements observés vis-à-vis de la consommation d’alcool chez les 16-25 ans à ce qui se serait passé sans l’implantation de cette politique.
| Model 1 Beta (IC 95 %) |
Model 2 Beta (IC 95%) |
Model 3 Beta (IC 95%) |
Model 4 Beta (IC 95%) |
|
|
Intercept |
2.23 (2,21 à 2.24) | 2.21 (2,19 à 2.24) | 2.12 (2,07 à 2.18) | 2.14 (2,02 à 2.25) |
|
Loi |
||||
|
Non |
1 | 1 | 1 | |
|
Oui |
-1,11 (-1,08 à -1,13) | -1,11 (-1,13 à -1,08) | -0,32 (-0,39 à -0,24) | -0,32 (-0,39 à -0,24) |
|
Années |
||||
|
2009 |
1 | 1 | ||
|
2010 |
0.04 (0,00 à 0.07) | 0.03 (-0,01 à 0.06) | 0.03 (-0,01 à 0.06) | |
|
2011 |
0.04 (0,00 à 0.07) | 0.04 (0,00 à 0.07) | 0.04 (0,00 à 0.07) | |
|
2012 |
-0.02 (-0,06 à 0.01) | -0,04 (-0,07 à 0.00) | -0,04 (-0,07 à 0.00) | |
|
Connaissance |
0.00 (-0,01 à 0.00) | |||
|
Âge |
0.00 (-0,01 à 0.00) |
* Il est commun de ne pas présenter les résultats de l’effet fixe pour les États. Nous ne représentons donc pas les coefficients pour chaque État. L’État 20 est exclu du modèle à cause de la colinéarité avec la loi et le temps.
La méthode de « régression avec discontinuité »
Présentation générale de la méthode de RD
La méthode dite de régression avec discontinuité (RD) peut être utilisée lorsqu’une intervention se base sur un seuil précis d’une variable continue pour déterminer l’éligibilité quant à cette intervention. Ce seuil peut être l’âge (comme dans notre exemple), un niveau de revenu (Andalón 2011) ou des marqueurs biologiques tels que les CD4, cellules du système immunitaire impactées par le VIH (Bor, Moscoe et al. 2014) par exemple. Tous les individus d’un côté du seuil recevront l’intervention tandis que tous ceux de l’autre côté de ce seuil ne la recevront pas. L’idée générale de cette approche est de considérer comme interchangeables les individus très proches d’une part et de l’autre de ce seuil, considérant le choix du seuil à sa valeur précise comme aléatoire. Le groupe contrefactuel est ainsi construit à partir d’une situation dans laquelle il n’y aurait aucune discontinuité au niveau du seuil d’éligibilité de l’intervention. Ainsi, il sera possible d’inférer qu’une différence dans les issues de santé entre les deux groupes sera la cause de la mise en place de ce seuil. Plusieurs étapes sont nécessaires pour mener à bien une analyse de type RD afin de vérifier plusieurs hypothèses quant à l’interchangeabilité entre les deux groupes, et le choix des modèles de régressions. Ces sept étapes sont détaillées ci-dessous.
Description des données
L’objectif de notre étude est d’estimer l’impact de l’âge légal sur la consommation d’alcool chez les jeunes. Afin de présenter l’application de la méthode de régression avec discontinuité, nous avons créé une base de données simulée. La base de données simulée contient des données pour 1 000 personnes âgées de 19 à 23 ans. De la même manière que pour l’analyse DD, aucune pondération n’a été incluse dans les analyses ici, mais cela demeure toutefois possible.
Nous avons une variable d’intérêt qui est la consommation d’alcool. Nous avons des données pour 1 000 personnes âgées de 19 à 23 ans.
La base de données contient les cinq variables suivantes :
- id : l’identificateur unique pour les répondant-e-s.
- âge : une variable qui indique l’âge du répondant ou de la répondante.
- propAlcJour : nombre de consommation d’alcool par jour du répondant ou de la répondante.
- fruit : consommation de fruits et légumes par semaine.
- cigarette : consommation de cigarettes par semaine.
Application de la méthode RD en sept étapes
1. Définir le seuil
Les données requièrent un seuil dans la probabilité de consommation par rapport à une variable continue d’attribution. Dans notre exemple, l’âge est la variable d’attribution. Ici, l’âge de majorité est 21 ans. Donc, avant 21 ans la consommation d’alcool n’est pas légale et après 21 ans elle est légale. Ceci constitue une rupture nette à l’âge de 21 ans.
2. Vérifier qu’il n’y a pas de biais ou erreur de mesure pour la variable d’intérêt par rapport au seuil
Un biais ou erreur de mesure pour la variable d’intérêt par rapport au seuil créera un biais systématique dans les estimations par la méthode RD. Par exemple, si la consommation d’alcool est sous-estimée chez les participant-e-s âgés de moins de 21 ans, soit parce que les répondant-e-s ne donnent pas des réponses réelles (ou refusent de répondre) puisque le comportement est illégal, l’estimé RD est biaisé de façon systématique (Imbens and Lemieux 2008). Dans notre cas, nous présumons qu’il n’y a pas de biais ou erreur de mesure pour la variable d’intérêt.
3. Vérifier que la variable d’attribution est continue et mesurée précisément
Dans la troisième étape, nous visualisons un histogramme, un graphique « Q-Q », et nous menons un test Shapiro-Wilk afin de nous assurer que la variable d’attribution continue est uniformément distribuée. Une variable d’attribution qui n’est pas continue posera problème dans le contexte de la méthode régression avec discontinuité, puisqu’il est possible que plusieurs seuils existent. Ainsi, si la variable d’attribution et plusieurs seuils existent, il n’est pas possible d’identifier un effet causal puisqu’un effet est possible à chaque seuil. La variable âge dans notre échantillon est uniforme.
4. Visualiser la variable d’attribution par la variable d’intérêt
Dans la quatrième étape, nous visualisons la variable d’attribution sur l’axe X avec les variables d’intérêts sur l’axe Y. La figure 2 présente ces relations. Nous présentons les données complètes avant et après l’âge de 21 ans en utilisant des options de graphique particulières. Le « smoothing » loess est le graphique créé par défaut par la commande rdrobust avec « binning » (mimicking variance evenly–spaced method using spacings estimators) et « smoothing » avec un polynomial du 4iéme ordre. Il est recommandé de présenter un graphique avec les données « binned » (Calonico, Cattaneo et al. 2015).
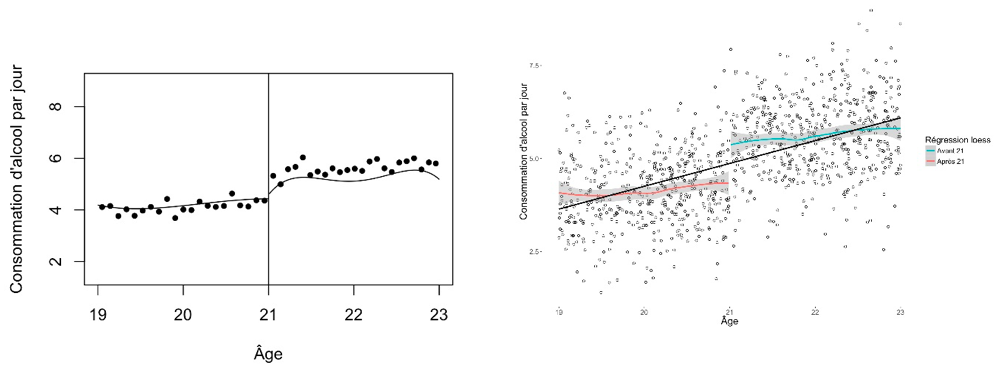
5. Comparaison de variable d’intérêt et co-variables
Dans la cinquième étape, nous voulons vérifier que les deux groupes sont interchangeables, sauf pour la variable sanitaire d’intérêt. Nous comparons la moyenne et l’écart-type de la variable d’intérêt avant et après 21 ans. Nous examinons aussi ceci pour deux co-variables que sont la consommation de fruits et légumes et la consommation de cigarettes (tableau 2). Étant donnée la prémisse que la politique influence seulement la consommation d’alcool, la politique ne devrait pas influencer d’autres comportements. L’idée de cette étape est de s’assurer qu’à part pour la consommation d’alcool, il n’y a pas d’autre discontinuité au même seuil (c’est-à-dire à 21 ans) pour d’autres variables dans l’échantillon.
|
|
Avant 21 ans |
Après 21 ans |
|
Alcool |
4.2 (1,0) |
5.6 (1,0) |
|
Fruit |
7.5 (4,5) | 7.6 (4,3) |
|
Cigarette |
39.0 (22,0) |
40.0 (23,0) |
6. Sélectionner l’étendue de l’échantillon sélectionné
Une prémisse importante de la méthode RD est que les groupes d’un côté et de l’autre du seuil sont interchangeables. Cela signifie qu’ils doivent être similaires pour toute autre caractéristique que la variable d’attribution (l’âge dans notre exemple) et la variable sanitaire d’intérêt. Il y a plusieurs méthodes proposées pour sélectionner le « bandwidth ». Le « bandwidth » définit l’étendue de l’échantillon sélectionné pour la régression. Il est très important puisqu’il définit la plausibilité que les groupes d’un côté et de l’autre du seuil soient interchangeables. Le « bandwidth » est typiquement estimé avec une estimation par noyau. Ici, nous proposons deux méthodes de sélections, à savoir MSE [Mean Square Error Optimal Bandwidth Selector] et CER [Coverage Error Rate Optimal Bandwidth Selector]) (Imbens and Kalyanaraman 2011, Calonico, Cattaneo et al. 2015) et trois différentes méthodes d’estimation par noyau (triangulaire, Epanechnikov et uniforme). Les méthodes de sélections de bandwidth sont disponibles avec le programme rdrobust pour R (Calonico, Cattaneo et al. 2015) et Stata (Calonico, Cattaneo et al. 2014).
Le choix de bandwidth peut avoir un impact sur la taille et l’échantillon afin de respecter le fait que les deux groupes d’un côté et de l’autre du seuil sont interchangeables. Dans notre exemple, notre échantillon de 1 000 répondant-e-s n’est pas affecté par le choix de bandwidth avec 484 droites et 516 gauches répondants inclus dans l’analyse pour une sélection bandwidth IK MSE avec une estimation par noyau triangulaire ou une sélection bandwidth CT avec une estimation par noyau uniforme (voir tableau 3 pour les résultats complets).
Dans notre cas, nous allons choisir la méthode MSE avec l’estimation par noyau triangulaire pour les analyses, c’est-à-dire la méthode par défaut sous R avec rdrobust. Quel que soit le choix, il est nécessaire de faire des analyses de sensibilité afin de s’assurer que le résultat n’est pas affecté par le choix du modèle.
7. Estimer l’effet de la politique publique par des modèles de régression
D’abord, nous estimons l’effet de la politique avec une régression linéaire sur l’échantillon complet. L’estimation pour la régression linéaire est une augmentation de la consommation d’alcool de 0,6 par semaine (IC 95 % 0.6 à 0,7). Avec l’échantillon complet, la prémisse que les groupes d’un côté et de l’autre du seuil sont interchangeables est moins plausible. Afin d’estimer un effet plausible, nous estimons la régression avec discontinuité avec la méthode MSE et l’estimation par noyau triangulaire. La régression inclut désormais 484 répondants à la gauche (avant 21 ans) et 516 répondants à la droite (après 21 ans) (tableau 4). La régression est estimée avec une régression locale linéaire et correction locale quadratique. L’estimation n’est pas influencée par la méthode de sélection du « bandwidth », ce qui indique que le résultat est robuste.
| Bandwidth MSE | Bandwidth CER | |
| Beta (IC 95 %) | Beta (IC 95 %) | |
| Conventional | 0.88 (0,2 à 1,5) | 0.80 (0,0 à 1,6) |
| Bias-Corrected | 0.80 (0,2 à 1,4) | 0.75 (-0,0 à 1,5) |
| Robuste | 0.80 (0,0 à 1,6) | 0.75 (-0,1 à 1,6) |
Les résultats montrent que le fait d’appartenir au groupe d’âge ayant le droit de consommer de l’alcool augmente d’environ une unité de consommation d’alcool par semaine (IC 95 % 0,2 à 1.5). Les analyses de sensibilité (CER avec correction pour le biais et robuste) démontrent qu’il est possible que l’estimation soit sensible au choix de modèle. Le chercheur ou la chercheuse doit être prudent-e dans l’interprétation et la communication des résultats.
Conclusion
Nous avons pu estimer, en utilisant la méthode de RD, l’effet de l’âge légal minimum de consommation d’alcool sur la consommation d’alcool chez les 19-23 ans. Nous avons trouvé que la consommation d’alcool augmente d’une unité de consommation par semaine quand l’on passe de 20 à 21 ans, ce qui montre que cette politique publique a un effet sur la consommation d’alcool chez les 19-23 ans.
En utilisant les contrastes entre les 19 à 20 et les 21 à 23 ans, nous avons pu construire un contre-factuel qui nous a permis de comparer les changements observés vis-à-vis de la consommation d’alcool chez les 19-23 ans avec ce qui serait passé sans la mise en place de cette politique publique.
Discussion
Dans ce chapitre, nous avons présenté deux méthodes quasi-expérimentales dans le contexte d’évaluation des effets de politiques publiques sur la santé. Nous avons montré que ces approches pouvaient constituer de bonnes solutions lorsque des essais contrôlés randomisés sont impossibles à mener. Nous avons principalement présenté deux approches, soit la méthode de différence dans les différences et l’approche de régression avec discontinuité. Ces deux approches permettent d’exploiter des situations d’expérimentations naturelles différentes. Nous avons, dans un premier temps, utilisé pour la méthode de différence dans les différences la date d’implantation de l’intervention pour comparer les changements concernant des indicateurs de santé avec le groupe contrôle. Dans le cas de l’approche de régression avec discontinuité, nous avons plutôt exploité un caractère spécifique de l’intervention, à savoir l’âge légal de consommation d’alcool. Ces deux approches visent à répondre à la même question, mais la différence principale réside dans l’effet qui est estimé et la population à laquelle ces résultats peuvent être généralisés. Dans le premier cas, nous quantifions un effet moyen total (Average Treatment Effect) qui prend la population dans son ensemble (il est important de noter qu’il est aussi possible de quantifier l’effet sur des sous-groupes de la population). Dans le second cas, nous quantifions un effet moyen total local (Local Average Treatment Effect) au sein de la population incluse dans l’analyse (à savoir les personnes aux âges 19-23 ans) si bien que les résultats ne sont pas extrapolables aux autres groupes d’âge notamment.
L’ensemble des étapes nécessaires pour conduire ce type d’analyse ainsi que les hypothèses à vérifier ont été décrites. Ces approches, particulièrement développées dans le domaine de l’économétrie, ont beaucoup été utilisées pour évaluer l’efficacité d’interventions sur la santé dans des pays à bas et moyen revenus, notamment en ce qui concerne des programmes de transferts de fonds (conditionnels ou non) (Andalón 2011) ou de programme d’accès aux soins (Dimick et Ryan 2014). Il est important de préciser qu’il est possible de conduire ce type d’évaluation en utilisant des données déjà collectées dans les pays à bas et moyen revenus, permettant ainsi la conduite de nombreuses recherches dans le futur.
Dans ce chapitre, nous avons abordé uniquement un type d’évaluation, à savoir l’évaluation des effets ou des impacts d’une politique publique, mobilisant la notion d’inférence causale. Inévitablement, ce type d’évaluation est complémentaire d’autres types, telles que les évaluations d’implantation qui mobilisent des méthodologies différentes. Enfin, nous avons abordé ici l’impact sanitaire de politiques publiques sur une population d’étude dans son ensemble. Pourtant, il est possible, voire systématique que les effets d’une politique publique ne soient pas distribués de manière homogène au sein de plusieurs sous-groupes d’une population. Cet aspect, à travers la notion d’équité, est ainsi abordé dans le chapitre suivant.
Références clés
Angrist, J. D. et Pischke, J.-S. (2014). Mastering metrics : The Path from Cause to Effect. Lieu d’édition : Princeton University Press.
Cet ouvrage est une excellente introduction aux méthodes quasi-expérimentales et autres approches couramment utilisées en économétrie et en épidémiologie. Il constitue une version plus accessible que l’ouvrage Mostly harmless econometrics: An empiricist’s companion (Princeton University Press, 2008) par les mêmes auteurs, plus détaillé mais plus difficile d’accès.
Bor, J. (2016). Capitalizing on natural experiments to improve our understanding of population health. American Journal of Public Health, 106(8), 1388.
Cet article, très court et facile d’accès, constitue un très bon résumé de la notion d’expérimentations naturelles et comment leur exploitation peut constituer d’excellentes alternatives aux essais contrôlés randomisés.
Deaton, A. et Cartwright, N. (2017). Understanding and misunderstanding randomized controlled trials. Social Science et Medicine, volume(numéro), p.-p.
Cet article résume de nombreux travaux des dernières années visant à expliciter ce que sont et surtout ne sont pas les essais contrôlés randomisés. Cet article, et les nombreux commentaires l’accompagnant, sont à lire pour comprendre les limites et les avantages de ce type d’approche qui est malheureusement trop souvent mal compris et mobilisé.
Références
Andalón, M. (2011). Oportunidades to reduce overweight and obesity in Mexico? Health economics, 20(S1), 1-18.
Angrist, J. D. et Pischke, J.-S. (2008). Mostly harmless econometrics: An empiricist’s companion. Princeton : Princeton University Press.
Angrist, J. D. et Pischke, J.-S. (2014). Mastering metrics : The path from cause to effect. Princeton : Princeton University Press.
Austin, P. C. (2011). An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivariate behavioral research, 46(3), 399-424.
Belaid, L. et Ridde, V. (2012). An implementation evaluation of a policy aiming to improve financial access to maternal health care in Djibo district, Burkina Faso. BMC pregnancy and childbirth, 12(1), 1.
Benmarhnia, T., Zunzunegui, M.-V., Llácer, A. et Béland, F. (2014). Impact of the economic crisis on the health of older persons in Spain: research clues based on an analysis of mortality. SESPAS report 2014. Gaceta Sanitaria. 28, 137-141.
Bonell, C. P., Hargreaves, J., Cousens, S., Ross, D., Hayes, R., Petticrew, M. et Kirkwood, B. (2011). Alternatives to randomisation in the evaluation of public health interventions: design challenges and solutions. Journal of Epidemiology and Community Health, 65(7): 582-587.
Bor, J. (2016). Capitalizing on natural experiments to improve our understanding of population health. American Journal of Public Health, 106(8), 1388.
Bor, J., Moscoe, E., Mutevedzi, P., Newell, M.-L. et Bärnighausen, T. (2014). Regression discontinuity designs in epidemiology: causal inference without randomized trials. Epidemiology, 25(5), 729-737.
Brousselle, A., Benmarhnia, T. et Benhadj, L. (2016). What are the benefits and risks of using return on investment to defend public health programs?. Preventive Medicine Reports, 3, 135-138.
Brousselle, A. et Lessard, C. (2011). Economic evaluation to inform health care decision-making: promise, pitfalls and a proposal for an alternative path. Social science et medicine,72(6), 832-839.
Calonico, S., Cattaneo, M. D. et Farrell, M. H. (2015). On the effect of bias estimation on coverage accuracy in nonparametric inference. Journal of the American Statistical Association, 113(522), 767-779.
Calonico, S., Cattaneo, M. D. et Titiunik, R. (2014). Robust data-driven inference in the regression-discontinuity design. Stata Journal, 14(4), 909-946.
Calonico, S., Cattaneo, M. D. et Titiunik, R. (2015). Optimal data-driven regression discontinuity plots. Journal of the American Statistical Association, 110(512), 1753-1769.
Calonico, S., Cattaneo, M. D. et Titiunik, R. (2015). rdrobust: An r package for robust nonparametric inference in regression-discontinuity designs. R Journal,7(1), 38-51.
Carpenter, C. et Dobkin, C. (2009). The effect of alcohol consumption on mortality: regression discontinuity evidence from the minimum drinking age. American Economic Journal: Applied Economics, 1(1), 164-182.
Carpenter, C. et Dobkin, C. (2011). The minimum legal drinking age and public health. The Journal of Economic Perspectives, 25(2), 133-156.
Champagne, F., Contandriopoulos, A.-P., Brousselle, A., Hartz, Z. et Denis, J.-L. (2009). L’évaluation dans le domaine de la santé : concepts et méthodes. In L’évaluation : Concepts et méthodes. Montréal : Presses de l’Université de Montréal.
Cook, T. D., Campbell, D. T. et Day, A. (1979). Quasi-experimentation : Design et analysis issues for field settings. Boston : Houghton Mifflin.
Dimick, J. B. et Ryan, A. M. (2014). Methods for evaluating changes in health care policy: the difference-in-differences approach. Jama, 312(22), 2401-2402.
Donald, S. G. et Lang, K. (2007). Inference with difference-in-differences and other panel data. The review of Economics and Statistics, 89(2), 221-233.
Drummond, M. F., Sculpher, M. J., Claxton, K., Stoddart, G. L. et Torrance, G. W. (2015). Methods for the economic evaluation of health care programmes. Lieu d’édition : Oxford University Press.
Fuller, D., Sahlqvist, S., Cummins, S. et Ogilvie, D. (2012). The impact of public transportation strikes on use of a bicycle share program in London: interrupted time series design. Preventive medicine, 54(1), 74-76.
Hawe, P., Shiell, A. et Riley, T. (2004). Complex interventions: how “out of control” can a randomised controlled trial be?. Penelope, 328, 1561-1563.
Hernán, M. A. et Robins, J. M. (2006). Instruments for causal inference: an epidemiologist’s dream?. Epidemiology, 17(4), 360-372.
Hilbe, J. M. (2011). Negative binomial regression. Cambridge : Cambridge University Press.
Holland, P. W. (1986). Statistics and causal inference. Journal of the American statistical Association, 81(396), 945-960.
Imbens, G. et Kalyanaraman, K. (2011). Optimal bandwidth choice for the regression discontinuity estimator. The Review of economic studies, 79(3), 933-959.
Imbens, G. W. et Lemieux, T. (2008). Regression discontinuity designs: A guide to practice. Journal of Econometrics, 142(2), 615-635.
Kaufman, J. S. (2007). Making causal inferences about macrosocial factors as a basis for public health policies. Macrosocial Determinants of Population Health, chapter 17, 355-373.
Kontopantelis, E., Doran, T., Springate, D. A., Buchan, I. et Reeves, D. (2015). Regression based quasi-experimental approach when randomisation is not an option: interrupted time series analysis. British Medical Journal, 350, h2750.
Macintyre, S. (2010). Good intentions and received wisdom are not good enough: the need for controlled trials in public health. Journal of Epidemiology and Community Health, 65(7), 564-567.
Moore, L. et Moore, G. F. (2011). Public health evaluation: which designs work, for whom and under what circumstances?. Journal of Epidemiology and Community Health, 65(7), 596-597.
Naimi, A. I. et Kaufman, J. S. (2015). Counterfactual theory in social epidemiology: reconciling analysis and action for the social determinants of health. Current Epidemiology Reports, 2(1), 52-60.
Newhouse, J. P. et McClellan, M. (1998). Econometrics in outcomes research: the use of instrumental variables. Annual Review of Public Health, 19(1), 17-34.
Pearl, J. (2009). Causality. Cambridge : Cambridge University Press.
Petticrew, M., Chalabi, Z. et Jones, D. R. (2011). To RCT or not to RCT: deciding when ‘more evidence is needed’ for public health policy and practice. Journal of Epidemiology and Community Health, 66(5), 391-396.
Rehm, J., Gmel, G., Sempos, C. T. et Trevisan, M. (2003). Alcohol-related morbidity and mortality. Alcohol Research et Health, 27(1), 39-51.
Royall, R. M. (1991). Ethics and statistics in randomized clinical trials. Statistical Science, 6(1), 52-62.
Sabatier, P. et Mazmanian, D. (1980). The implementation of public policy: A framework of analysis. Policy Studies Journal, 8(4), 538-560.
Shadish, W. R. et Cook, T. D. (2009). The renaissance of field experimentation in evaluating interventions. Annual Review of Psychology, 60, 607-629.
Shadish, W. R., Luellen, J. K. et Clark, M. (2006). Propensity Scores and Quasi-Experiments: A Testimony to the Practical Side of Lee Sechrest. Dans R. R. Bootzin et P. E. McKnight (dir.), Strengthening research methodology: Psychological measurement and evaluation (p. 143-157). Washington, DC : American Psychological Association.
Susser, M. (2001). Glossary: causality in public health science. Journal of Epidemiology and Community Health, 55(6), 376-378.
Yörük, C. E. et Yörük, B. K. (2012). The impact of drinking on psychological well-being: Evidence from minimum drinking age laws in the United States. Social Science et Medicine, 75(10), 1844-1854.
Résumé / Abstract
Les méthodes quasi-expérimentales (MQE) sont des alternatives aux essais contrôlés randomisés, qui permettent, en se basant sur le modèle contre-factuel, d’évaluer les effets d’interventions en exploitant des expérimentations naturelles. L’objectif de ce chapitre est d’introduire deux MQE, à savoir la me la méthode de Différence dans les Différences (DD) ainsi que l’approche de Régression avec Discontinuité (RD). Leur application afin d’évaluer l’effet de l’âge légal minimum sur la consommation d’alcool chez les jeunes est ensuite présentée. Sont présentées toutes les étapes nécessaires et les codes statistiques (pour R et Stata) permettant de reproduire ce type d’analyse. Ces approches constituent de bonnes solutions lorsque des essais contrôlés randomisés sont impossibles ou difficiles à mener, permettant de s’assurer que des objectifs d’un programme de santé publique sont bel et bien atteints, de décider quant au maintien, à la modification ou à l’arrêt d’interventions existantes et de s’assurer que les ressources publiques sont utilisées de manière efficace.
***
Quasi-experimental methods have been developed to evaluate ‘natural experiments,’ an alternative design to randomized controlled trials that relies on the notion of the counterfactual to estimate causal effects. The objective of this chapter is to describe quasi-experimental methods, apply them empirically to an example, and provide all elements of the evaluation, allowing the reader to reproduce these analyses (in R and Stata) in their given context. The main objective of this type of policy evaluation is to attribute a causal effect of an intervention on a health indicator. We apply these methods to estimate the impact of a policy raising minimum legal drinking on alcohol consumption among young people. Two types of quasi-experimental methods are used in this evaluation: the Difference in Differences (DD) method and the discontinuous regression (RD) approach. We show that these approaches can be good solutions to evaluate policies when randomized controlled trials are impossible. These evaluation tools can be used to ensure that policies contribute to the improvement of population health, to inform and decide whether to maintain, modify or discontinue existing interventions and to ensure public resources are used effectively.
***
Se han desarrollado métodos cuasi-experimentales para evaluar los « experimentos naturales », un diseño alternativo a los ensayos controlados aleatorios que se basa en la noción de lo contrafactual para estimar los efectos causales. El objetivo de este capítulo es describir métodos cuasi-experimentales, aplicarlos empíricamente a un ejemplo y proporcionar todos los elementos de la evaluación, permitiendo al lector reproducir estos análisis (en R y Stata) en su contexto dado. El objetivo principal de este tipo de evaluación de políticas es atribuir un efecto causal de una intervención a un indicador de salud. Aplicamos estos métodos para estimar el impacto de una política que aumenta el consumo mínimo legal de alcohol en el consumo de alcohol entre los jóvenes. En esta evaluación se utilizan dos tipos de métodos cuasiexperimentales: el método de la Diferencia de Diferencias (DD) y el enfoque de regresión discontinua (RD). Demostramos que estos enfoques pueden ser buenas soluciones para evaluar las políticas cuando los ensayos controlados aleatorios son imposibles. Estas herramientas de evaluación pueden utilizarse para garantizar que las políticas contribuyan a mejorar la salud de la población, para informar y decidir si se mantienen, modifican o interrumpen las intervenciones existentes y para garantizar que los recursos públicos se utilicen de manera eficaz.
***
Tarik Benmarhnia est Professeur Assistant d’épidémiologie à l’Université de Californie à San Diego au sein de l’Institut d’océanographie Scrippset de l’école de médecine. Il a complété son doctorat en épidémiologie à l’Université de Montréal et à l’Université Paris Sud. Il est également chercheur associé au Chili et en France et membre du comité éditorial de Environmental Health Perspectives. Sa recherche porte sur les impacts des événements extrêmes sur la santé avec un focus sur les populations vulnérables et les implications en termes de politiques publiques. Il développe également des approches méthodologiques pour évaluer l’effet des politiques environnementales sur la santé comme les mesures d’adaptation aux changements climatiques et mesures de contrôle de la pollution atmosphérique.
Daniel Fuller est titulaire d’une Chaire de recherche du Canada en activité physique populationnelle à l’Université Memorial de Saint-Jean de Terre-Neuve. Ses recherches portent sur les technologies portables afin d’étudier l’activité physique, les interventions en transports et l’iniquité dans les espaces urbains. Son travail méthodologique vise les méthodes d’expérimentation naturelle et l’apprentissage-machine. Dan est titulaire d’une maitrise en kinésiologie de l’Université de Saskatchewan, d’un doctorat en santé publique de l’Université de Montréal, et a effectué de la recherche postdoctorale au Département de santé communautaire et d’épidémiologie de l’Université de Saskatchewan. Daniel est co-directeur de l’équipe Neighbourhood Factors du Canadian Urban Environmental Health (CANUE) Research Consortium et chercheur principal de l’équipe INTERACT.
Citation
Tarik Benmarhnia et Daniel Fuller. (2019). Les méthodes quasi expérimentales. L’effet de l’âge légal minimum sur la consommation d’alcool chez les jeunes aux États-Unis. In Évaluation des interventions de santé mondiale. Méthodes avancées. Sous la direction de Valéry Ridde et Christian Dagenais, pp. 241-264. Québec : Éditions science et bien commun et Marseille : IRD Éditions.

