11 La mesure de l’équité
Un exemple d'intervention de gratuité des soins obstétricaux
Tarik Benmarhnia et Britt McKinnon
| Définition de la méthode Nous définissons l’équité des effets d’une intervention en fonction de l’identification d’une hétérogénéité dans les bénéfices potentiels entre différents sous-groupes ou territoires d’une population. Une intervention sera évaluée comme équitable si les bénéfices sont plus importants au sein des sous-groupes ou territoires qui auront été définis comme les plus vulnérables ou ayant les besoins les plus importants. |
| Forces de la méthode
La méthode proposée permet de quantifier les inégalités de santé pour plusieurs configurations (groupes ordonnés ou non) sur une échelle absolue ou relative. |
| Défis de la méthode
Il est important de disposer d’un bon niveau de connaissance des populations vulnérables et de bien les étudier empiriquement et théoriquement. Pour certaines des méthodes proposées (par exemple, les analyses de décomposition…), il est parfois nécessaire d’avoir de grands échantillons pour identifier une hétérogénéité dans les bénéfices potentiels d’une intervention au sein de deux ou plusieurs groupes. |
L’équité en santé est largement identifiée comme un objectif auquel les politiques et activités de santé publique doivent répondre en priorité (Starfield 2007; Marmot, Friel et al. 2008; Blas et Kurup 2010). Toutefois, il existe une grande diversité dans les définitions de la notion d’équité en santé et de telles implications sont amplement discutées (Whitehead 1992; Braveman et Gruskin 2003; Braveman, Cubbin et al. 2005). Parfois, cette notion, souvent définie via son opposé qui est l’inéquité ou iniquité, se réfère à la description de différences évitables ou remédiables entre différents groupes de personnes (Whitehead 1992; Kawachi, Subramanian et al. 2002), incluant donc une dimension morale et éthique (Daniels 2006; Smith 2015). Parfois, elle fait référence aux conséquences d’une intervention de santé publique. En effet, dans cette dernière dimension, la notion d’inéquité implique une intervention qui viendra accroitre des inégalités de santé déjà existantes. Ces deux notions sont parfois fusionnées, mais souvent les implications et hypothèses sur le plan des théories de justice sociale sous-jacentes sont trop peu discutées (Smith 2015).
Dans ce chapitre, nous proposons une définition de l’équité en santé qui fait référence à la distribution des bénéfices des politiques publiques.
Cette définition implique, dans un premier temps, l’identification des sous-groupes ou territoires d’une population pour lesquels l’état de santé sera considéré comme plus négatif ou au sein desquels l’impact d’un déterminant de la santé sera plus important (notion épidémiologique de modification d’effet) en comparaison à un autre sous-groupe ou territoire de la même population. Nous appellerons ces sous-groupes d’une population « populations vulnérables », en comparaison avec des populations non vulnérables.
Ainsi, dans ce chapitre, nous définissons l’équité des effets d’une intervention en fonction de l’identification d’une hétérogénéité dans les bénéfices potentiels entre différents sous-groupes ou territoires d’une population. Une intervention sera évaluée comme équitable si les bénéfices sont plus importants au sein des sous-groupes ou territoires qui auront été définis comme vulnérables.
La notion d’équité en santé est discutée depuis plusieurs décennies, mais relativement peu mise en œuvre. Entendue dans le contexte d’une distribution inégale des effets d’interventions de santé publique, son évaluation est minoritaire en comparaison avec l’évaluation des effets sur toute une population. Pour illustrer cela, nous pouvons prendre deux exemples. Les évaluations des effets des politiques publiques de lutte contre le tabagisme sont massivement étudiées dans la littérature épidémiologique (Hoffman et Tan 2015) et se comptent par centaines. Cependant, la grande majorité de ces études portent principalement sur une population dans son ensemble (Frazer, Callinan et al. 2016) ou sur un sous-groupe de la population comme les adolescent-e-s (Gilman, Rende et al. 2009) ou certains professionnel-le-s (Farrelly, Nonnemaker et al. 2005). Les études qui évaluent les inégalités des effets d’une politique publique de lutte contre le tabagisme entre deux ou plusieurs sous-groupes d’une population sont bien plus rares (Brown, Platt et al. 2014a; Brown, Platt et al. 2014b) et concernent par exemple les inégalités selon le sexe, l’âge ou le niveau d’éducation. Le deuxième exemple porte sur les interventions de lutte contre la pollution atmosphérique en milieu urbain (Cartier, Benmarhnia et al. 2015). Dans une revue systématique (Benmarhnia, Rey et al. 2014), nous avons pu mettre en évidence que sur plus de 50 études publiées, seulement deux études ont formellement évalué l’hétérogénéité des effets de l’intervention au sein de différents sous-groupes et huit études permettaient une évaluation a posteriori entre les estimations stratifiées. Ces deux exemples mettent en évidence, d’une part, le faible nombre d’études ayant investigué cette question de recherche spécifique, malgré la grande disponibilité des données permettant de mener de telles études, et d’autre part, le manque de méthodes appropriées permettant d’évaluer l’équité en santé, la plupart des études basant leurs conclusions sur des comparaisons qualitatives entre différentes strates de population ou via un test d’interaction dans un modèle de régression.
Dans ce chapitre nous présentons différentes méthodes de mesures des inégalités de santé et leur application à l’évaluation des effets des interventions à travers l’exemple de l’effet de l’exemption du paiement des frais de soins sur l’accès aux soins obstétricaux dans le cadre d’un exemple simulé.
Nous présentons dans un premier temps le contexte d’évaluation en décrivant l’intervention considérée, les données étudiées et les justifications d’un potentiel effet hétérogène de cette intervention sur l’accès aux soins obstétricaux. Ensuite, nous présentons différentes méthodes pour mesurer les inégalités de santé et différentes approches pour les appliquer à l’évaluation des effets des interventions, donc à l’équité telle que définie dans ce chapitre.
Présentation du contexte d’évaluation de l’équité : l’exemple de l’exemption du paiement des frais de soins (gratuité des soins) et l’impact sur l’accès aux soins obstétricaux
L’accès aux soins de base demeure un enjeu fondamental dans de nombreux pays à faible et moyen revenus (Althabe, Bergel et al. 2008; Lagarde et Palmer 2008; Dzakpasu, Powell-Jackson et al. 2013; McKinnon, Harper et al. 2014; McKinnon, Harper et al. 2015). Dans le contexte de systèmes de santé largement sous-financés, ces pays se retrouvent face à un dilemme. D’une part, le paiement des frais de soins peut présenter une barrière financière à l’accès aux soins. D’autre part, une diminution des ressources financières des systèmes de santé peut contribuer à une baisse de la qualité des services de santé qui pourra aussi constituer des barrières financières à l’assistance qualifiée à l’accouchement. Certaines études ont montré que la mise en place du paiement des frais de soins contribue à augmenter les ressources au niveau local et à améliorer la qualité des services (Ellis 1987; Litvack et Bodart 1993). D’autres études ont montré des effets négatifs, notamment sur le plan de l’équité (Yoder 1989; Russell et Gilson 1997). De nombreuses campagnes internationales visant à promouvoir la gratuité des soins (par exemple l’exemption de la tarification des accouchements) ont été menées (Yates 2009; Ridde et Morestin 2011).
Dans ce contexte, nous proposons de prendre comme exemple d’intervention la mise en place de la gratuité des soins obstétricaux (c’est-à-dire l’exemption de la tarification des accouchements) et d’évaluer son impact et son équité quant à l’accès aux soins obstétricaux. Afin d’évaluer les effets vis-à-vis de l’équité, nous allons considérer deux dimensions quant à une potentielle hétérogénéité dans les bénéfices de cette intervention. Premièrement, nous allons considérer une dimension liée aux inégalités matérielles que nous allons mesurer par un indice de richesse (wealth index) souvent utilisé dans les enquêtes populationnelles internationales (Filmer et Pritchett 1999; Howe, Hargreaves et al. 2009). Deuxièmement, nous allons considérer une dimension liée aux inégalités sociales par la mesure du niveau d’éducation de la mère. Ce choix est justifié par les inégalités sociales et matérielles quant à l’accès aux soins obstétricaux dans un contexte de pays à faible et moyen revenus (Say et Raine 2007). Ainsi, nous définissons l’intervention comme équitable si elle contribue à réduire les inégalités matérielles et/ou sociales d’accès aux soins obstétricaux.
L’exemple que nous présentons ci-dessous provient de données simulées à partir d’enquêtes populationnelles et ne correspond pas à une situation réelle d’intervention. De nombreux exemples de ce type d’intervention existent (Lagarde et Palmer 2008). Nous nous concentrons sur les inégalités socio-économiques, mais la définition d’équité adoptée dans ce chapitre peut s’appliquer également à d’autres facteurs démographiques (âge, sexe, genre) ou territoriaux (urbain vs rural).
Méthodes pour mesurer les inégalités de santé
Un certain nombre d’indicateurs peuvent être utilisés pour mesurer les inégalités de santé. Toutefois, il n’existe pas de consensus quant à une mesure en particulier, notamment lorsqu’il s’agit de mesurer les variations d’inégalités dans le temps. Cette section commence par une discussion sur des enjeux importants quant à la mesure des inégalités, notamment sociales, en santé. Dans la section suivante, nous allons décrire différents indicateurs permettant de mesurer des inégalités de santé avec des exemples les illustrant.
Enjeux quant à la mesure des inégalités de santé
Inégalités absolues vs relatives
Il est important tout d’abord de bien distinguer les mesures d’inégalités relatives et absolues dans la mesure où elles fournissent toutes deux des informations importantes, mais fondamentalement différentes vis-à-vis de la présence et de l’ampleur d’inégalités. Les mesures absolues reflètent l’ampleur des différences de santé entre deux groupes. Par exemple, les taux de mortalité pour cause cardiovasculaire en 2014 étaient de 12 pour 1000 hommes et de 8 pour 1000 femmes, la mesure absolue d’inégalité serait de 4 pour 1000 x année. En parallèle, les mesures relatives reflètent une différence proportionnelle de santé entre deux groupes. Dans l’exemple précèdent, elle représenterait le ratio des deux taux, à savoir 12/8 = 1,5. Parce que ces deux mesures peuvent conduire à des conclusions distinctes vis-à-vis de l’ampleur et des changements concernant les inégalités, il est important de rapporter les deux échelles pour présenter un portrait complet des inégalités (Lynch, Smith et al. 2006; Houweling, Kunst et al. 2007; Harper, King et al. 2010).
Classifier les groupes sociaux
Certains groupements sociaux ont « naturellement » deux groupes (homme/femme, urbain/rural), tandis que d’autres groupes possèdent plusieurs niveaux (niveau d’éducation, ethnicité). Pour les groupements sociaux à plusieurs groupes, le choix des indicateurs d’inégalités à adopter se fera en fonction du fait que les groupes sont organisés selon une structure ordonnée ou non. Le niveau d’éducation ou le niveau d’indice de richesse constituent par exemple des groupements ordonnés, tandis que l’ethnicité ou des caractéristiques géographiques ne sont pas a priori ordonnées. Des comparaisons par paire peuvent systématiquement être menées entre deux groupes pour n’importe quel type de variable sociale. De plus, l’ampleur des inégalités sociales pour plusieurs groupes (ordonnés ou non) peut être mesurée à partir d’indicateurs plus complexes comme l’indice d’inclinaison des inégalités (slope index of inequalities) ou l’indice de Theil.
Mesures des inégalités de santé
Les indicateurs simples d’inégalités (comparaison par paires)
Les mesures standards pour comparer l’état de santé entre deux groupes sociaux sont la différence et le ratio. Ces deux mesures sont complémentaires. Si l’indicateur de santé est exprimé en taux (par exemple la mortalité par cancer pour 100 000 personnes par an), les mesures absolues et relatives correspondent respectivement à une différence de taux et un ratio de taux, comparant deux groupes sociaux d’intérêt.
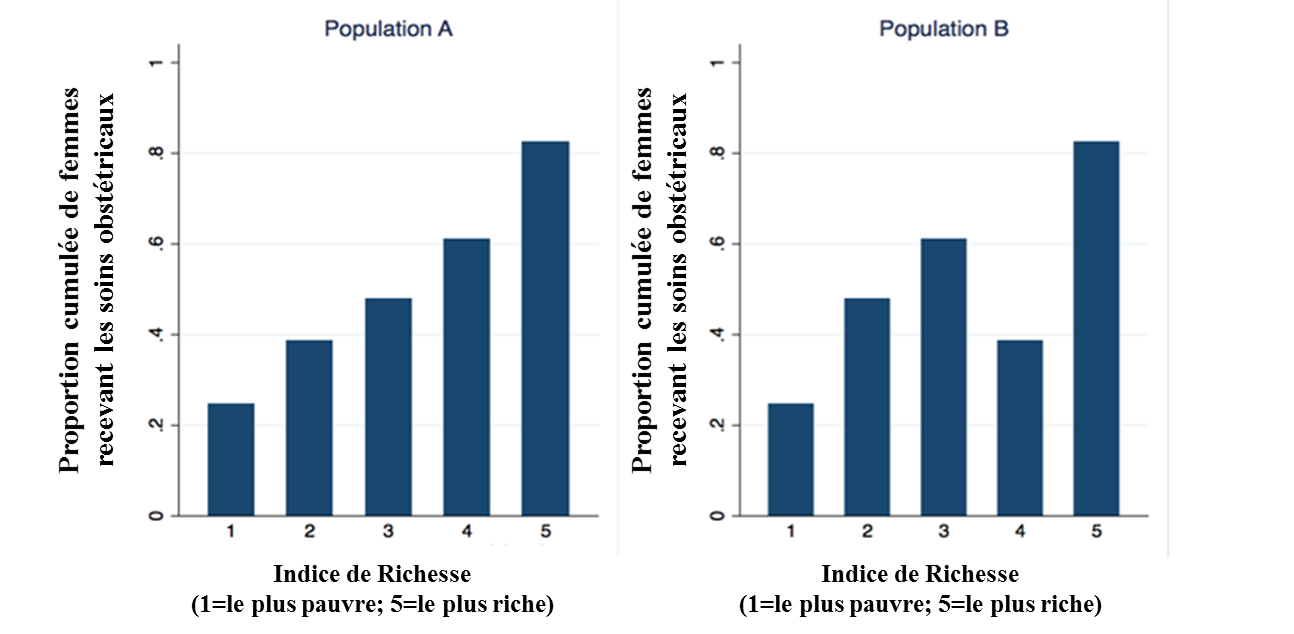
Pour les groupes sociaux ordonnés via le niveau d’éducation par exemple, les comparaisons par paires se font en général par la comparaison des groupes aux extrémités. Par exemple, si l’on considère un indice de richesse stratifié en quintiles, il s’agira de comparer le quintile le plus riche au quintile le plus pauvre. Pourtant, ce type de comparaison ignore l’état de santé des trois autres quintiles, qui peut fournir une information importante vis-à-vis d’inégalités au sein de la population. La figure 1 présente la proportion de femmes ayant reçu des soins obstétricaux auprès d’un-e professionnel-le qualifié-e par quintile d’un indice de richesse pour deux populations hypothétiques. Les deux populations ont les mêmes valeurs de différence ou de ratio en comparant les deux quintiles extrêmes, tandis que le portrait au sein des trois autres quintiles est différent. C’est la raison pour laquelle des mesures d’inégalités plus complexes, considérant l’ensemble des groupes, sont généralement préférées.
L’indice d’inclinaison des inégalités et l’indice de concentration sont deux mesures souvent utilisées pour mesurer le gradient de santé au sein de groupes sociaux ordonnés. Contrairement aux mesures simples présentées ci-dessus, ces indices prennent en compte la taille relative de chaque groupe.
L’indice d’inclinaison des inégalités
L’indice d’inclinaison des inégalités mesure la différence absolue par rapport à des valeurs prédites entre les groupes les plus hauts et les groupes les plus bas de la distribution de la position sociale pour des groupes ordonnés (éducation, indice de richesse, etc.) (Pamuk 1985). Cet indice est estimé à partir du modèle de régression approprié à la mesure de santé considérée (par exemple, une régression linéaire pour une mesure continue, et une régression logistique pour une mesure de santé binaire). Il est possible de calculer cet indice en utilisant l’indice de richesse en continu par exemple, en allant des plus pauvres (rang=0) aux plus riches (rang=1). La mesure de santé est ensuite incluse dans un modèle de régression en incluant, comme prédicteur, le rang de chaque individu au sein de la distribution cumulative de richesse. Ainsi, le coefficient correspondant à ce rang représentera la différence de santé estimée entre les plus pauvres et les plus riches individus de la population.
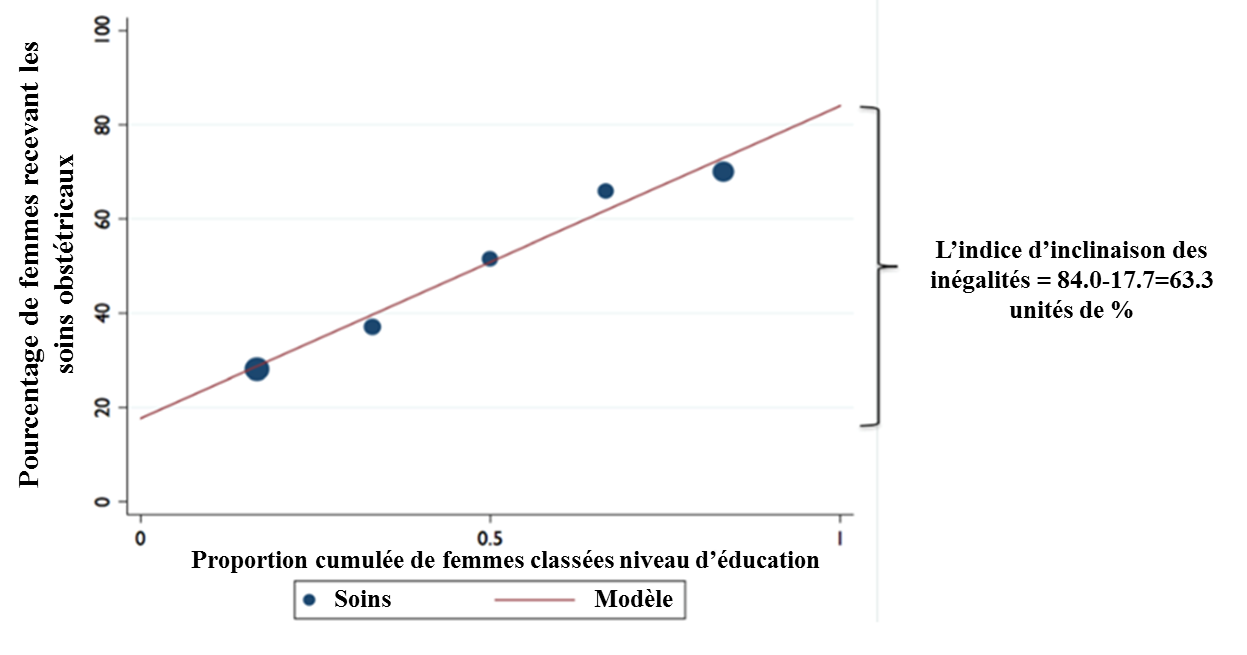
La figure 2 est une représentation graphique de cet indice, montrant la valeur prédite de l’issue de santé (ici le fait de recevoir des soins obstétricaux par un-e professionnel-le qualifié-e) en fonction de la proportion cumulée du rang par rapport au niveau d’éducation. La valeur prédite de prévalence de réception de soins obstétricaux (par un-e professionnel-le qualifié-e) parmi les femmes avec le plus bas niveau d’éducation (rang=0) est de 17,7%. Parmi les femmes avec le plus haut niveau (rang=1), cette valeur est de 84%. Ainsi, la valeur de cet indice sera de 84-17.7 = 66,3 en %, ce qui signifie que les femmes au plus haut de la distribution du niveau d’éducation ont 63% plus de chance de recevoir des soins obstétricaux par un-e professionnel-le qualifié-e en comparaison avec les femmes au plus bas de cette distribution.
Lorsque les individus sont classés des plus défavorisés au moins défavorisés, des valeurs positives de cet indice indiquent que la prévalence de la mesure de santé est plus importante au sein des individus les moins défavorisés alors qu’une valeur négative indique que cette prévalence est plus importante au sein des plus défavorisés. Une valeur de 0 signifie une égalité au sein du gradient social. Une mesure relative de cet indice peut également être estimée en calculant le ratio entre les valeurs prédites des deux extrémités de la distribution. Selon la figure 2, cet indice sur l’échelle relative serait de 84/17,7=4,7, signifiant que la réception de soins obstétricaux par un-e professionnel-le qualifié-e est 4,7 fois plus élevée au sein du groupe le plus favorisé en comparaison au groupe le moins favorisé.
L’indice de concentration
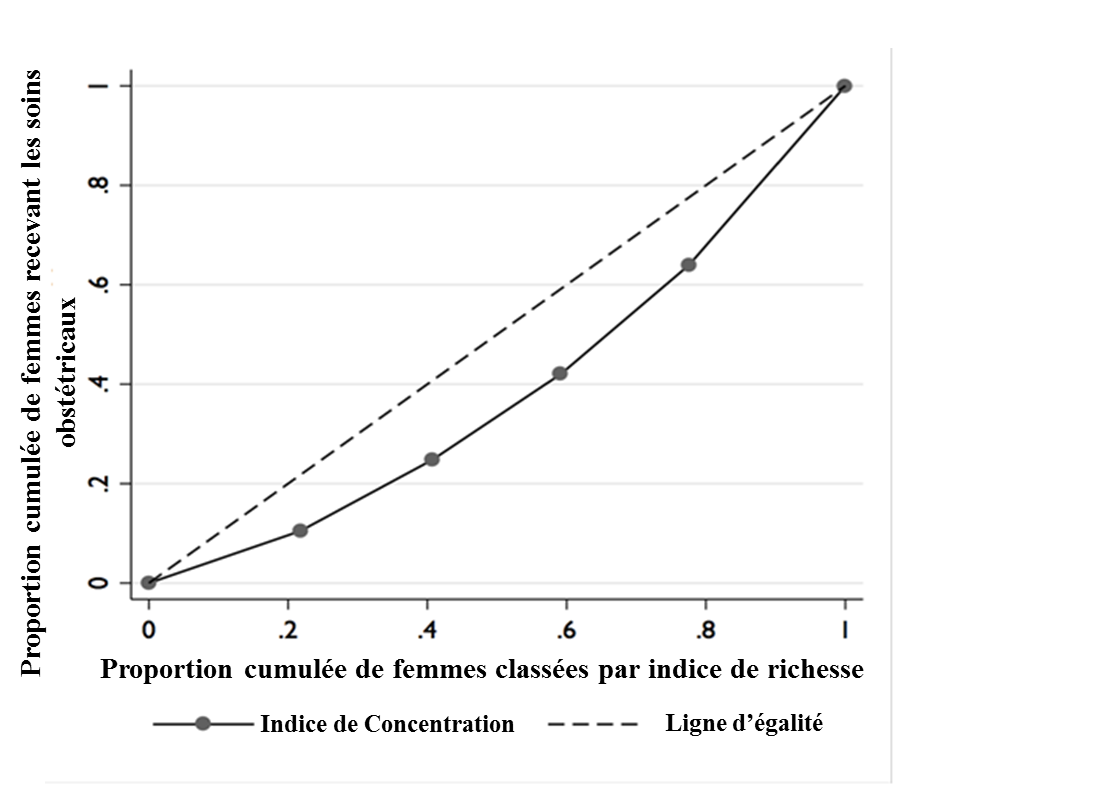
L’indice de concentration est une mesure relative des inégalités basée sur la courbe de concentration, une figure représentant la proportion cumulée d’individus classés par rang de santé sur l’axe X avec la proportion cumulée sur l’axe Y. La figure 3 représente la courbe de concentration avec les inégalités de richesse vis-à-vis de soins obstétriques utilisant les données présentées dans le tableau 1. La ligne à 45° représente la ligne d’égalité lorsque les ressources sont distribuées également au sein de la population. La courbe de concentration est située en dessous de cette ligne d’égalité, indiquant une inégalité défavorable aux femmes les plus pauvres. Par exemple, on peut observer que les 40% des femmes les plus pauvres ne bénéficient que de 25% à peu près du total des visites obstétricales.
|
Indice de Richesse |
Nombre de femmes |
Proportion de femmes |
Proportion cumulée de femmes |
Nombre de femmes recevant les soins |
Proportion de femmes recevant les soins |
Proportion cumulée de femmes recevant les soins |
| 1 | 1167 | 0,217 | 0,217 | 288 | 0,105 | 0,105 |
| 2 | 1017 | 0,190 | 0,407 | 394 | 0,143 | 0,248 |
| 3 | 990 | 0,184 | 0,592 | 475 | 0,172 | 0,420 |
| 4 | 989 | 0,184 | 0,776 | 604 | 0,219 | 0,640 |
| 5 | 1203 | 0,224 | 1,0 | 992 | 0,360 | 1,0 |
L’indice de concentration est défini comme le double de l’aire située entre la courbe de concentration et la ligne d’égalité (Wagstaff, Van Doorslaer et al. 1991). Cet indice peut se situer entre -1 et 1, avec 0 représentant une égalité complète. Des valeurs positives signifient des inégalités au détriment des plus pauvres pour une mesure de santé positive (comme dans cet exemple). Pour des données regroupées par quintile par exemple, comme dans le tableau 2, l’indice de concentration se calcule grâce à la formule suivante :
![]()
où pt est le pourcentage cumulé de l’échantillon classé par indice de richesse pour le groupe t, et Lt correspond la valeur de répartition de la mesure de santé par quintile (O’Donnell et Wagstaff 2008). Le tableau2 utilise les données de la courbe de concentration présentée ci-dessus et la dernière colonne présente le calcul de l’indice de concentration. Ici cet indice est de 0,224.
|
Indice de Richesse (t) |
Proportion cumulée de femmes par quintile de richesse (pt) |
Proportion cumulée de femmes recevant les soins (Lt) |
Indice de Concentration |
| 1 | 0,217 | 0,105 | 0,011 |
| 2 | 0,407 | 0,248 | 0,025 |
| 3 | 0,592 | 0,420 | 0,052 |
| 4 | 0,776 | 0,640 | 0,136 |
| 5 | 1,0 | 1,0 | 0,000 |
| 0,224 |
L’indice de concentration est une mesure d’inégalité relative, mais il est possible d’obtenir une version absolue de cet indice en multipliant l’indice de concentration obtenu par la moyenne de la mesure de santé. Il est aussi possible de calculer cet indice de concentration au niveau individuel en utilisant des approches basées sur des régressions[1]
Un enjeu important dans la recherche portant sur les inégalités de santé concerne la compréhension des facteurs qui contribuent le plus aux inégalités par rapport à une mesure de santé donnée. Un avantage de cet indice est qu’il peut être utilisé dans le cadre d’analyses de décomposition. Ce type d’analyses quantifie la contribution de différents facteurs quant à des inégalités sociales vis-à-vis d’une mesure de santé. Plusieurs exemples existent dans la littérature allant de la compréhension des déterminants des inégalités sociales de l’obésité au Canada (Hajizadeh, Campbell et al. 2014) à celle des inégalités sociales de mortalité infantile en Iran (Hosseinpoor, Van Doorslaer et al. 2006)[2].
Mesures complexes des inégalités avec groupes non ordonnés – l’indice de Theil
Les deux indices présentés ci-dessus sont valables uniquement lorsque les groupes sociaux sont ordonnés. Lorsque les groupes sociaux ne sont pas ordonnés, il est possible d’utiliser l’indice de Theil (Theil 1967). Les mesures d’inégalités absolues pour des catégories non-ordonnées incluent la méthode de variance (Harper, Lynch et al. 2008) entre groupes et l’indice de disparité (Pearcy et Keppel 2002) récemment étendue aux analyses de séries temporelles (Benmarhnia, Grenier et al. 2015).
L’indice de Theil est estimé à partir de la formule ![]() où pi est la proportion de la population dans le groupe social i et ri est le ratio de la moyenne de la mesure de santé dans le groupe i par rapport à la moyenne pour l’ensemble des groupes. Ainsi, si chaque groupe a une valeur moyenne de la mesure de santé égale à la moyenne pour tous les groupes, alors il n’y a pas d’inégalité relative et l’indice de Theil sera égal à 0. Cet indice est toujours positif. Plus sa valeur est grande, plus le niveau d’inégalité relative entre les groupes est important.
où pi est la proportion de la population dans le groupe social i et ri est le ratio de la moyenne de la mesure de santé dans le groupe i par rapport à la moyenne pour l’ensemble des groupes. Ainsi, si chaque groupe a une valeur moyenne de la mesure de santé égale à la moyenne pour tous les groupes, alors il n’y a pas d’inégalité relative et l’indice de Theil sera égal à 0. Cet indice est toujours positif. Plus sa valeur est grande, plus le niveau d’inégalité relative entre les groupes est important.
Les données dans le tableau 3 montrent comment calculer l’indice de Theil pour mesurer une inégalité relative d’accès aux soins obstétricaux au sein de cinq régions géographiques distinctes.
|
Région |
Soins obstétricaux (%) |
Proposition de population (pi) |
Ratio de % de soins dans la région par rapport à la population totale (ri) |
ln(ri) |
Indice de Theil |
| A | 45,8 | 0,29 | 0,90 | -0,11 | -0,028 |
| B | 55,7 | 0,12 | 1,09 | 0,09 | 0,011 |
| C | 48 | 0,18 | 0,94 | -0,06 | -0,010 |
| D | 82,5 | 0,22 | 1,62 | 0,48 | 0,175 |
| E | 22,8 | 0,19 | 0,45 | -0,81 | -0,067 |
| Toutes régions | 51,0 | 0,081 |
Dans cette section, nous avons présenté un portrait de différentes mesures d’inégalités de santé. Il ne s’agit ni d’une liste exhaustive des mesures existantes pour mesurer les inégalités de santé, ni d’une discussion approfondie des enjeux conceptuels. Pour ce dernier point, nous recommandons les travaux de Kawachi et Kennedy (1997), Mackenbach et Kunst (1997) et Regidor (2004). Toutefois, nous avons pu présenter plusieurs cas de figure qui pourront ensuite être utilisés pour évaluer la distribution des effets d’interventions de santé publique tels que décrits dans la section suivante.
Application aux études d’évaluation des effets
Dans cette partie, nous allons présenter comment appliquer les méthodes de mesures des inégalités présentées ci-dessus à l’évaluation des effets d’une intervention de santé publique.
Nous présentons deux types d’approches : une approche d’évaluation simple permettant d’illustrer facilement les méthodes présentées ci-dessus et qui nous permettra également d’introduire les tests d’hétérogénéité et une approche basée sur les designs quasi-expérimentaux. Les détails des méthodes d’évaluation, particulièrement quant aux approches quasi-expérimentales, sont présentés dans le chapitre précédent.
Approches simples de type avant/après
Une première approche simple permettant d’évaluer si les bénéfices d’une intervention (ici la mise en place de la gratuité des soins obstétricaux) sont équitables est de comparer si les inégalités d’accès aux soins obstétricaux entre différents groupes sont modifiées avant et après la mise en place de l’intervention. Nous pouvons prendre comme exemple la comparaison du premier quintile de l’indice de richesse au cinquième quintile de cet indice. Ainsi en calculant la différence ou le ratio entre ces deux groupes, d’une part, avant la mise en place de l’intervention et, d’autre part, après sa mise en place, nous pouvons obtenir deux mesures (sur l’échelle absolue ou relative) d’inégalités d’accès aux soins obstétricaux. Il suffit ensuite de mener un test d’hétérogénéité entre ces deux mesures pour évaluer si les bénéfices ont été distincts entre les deux groupes et dans quelle direction. Il existe de nombreux tests d’hétérogénéité qui peuvent être menés dans ce contexte. Nous proposons comme exemple le Cochran Q test (Kaufman et MacLehose 2013). Ce test peut être conduit sur des mesures absolues ou relatives. Ce test d’hétérogénéité est construit de la manière suivante. Si l’on considère par exemple l’échelle relative et le ratio de prévalence (RP) comme mesure d’association, nous devons estimer un RP qui représente l’effet de l’intervention pour chacun des groupes (ratio de la prévalence d’accès aux soins obstétricaux avant et après l’intervention) RP1 et RP2 et pour les deux groupes ensemble (RPp). Ensuite, il suffit de calculer l’estimé Cochran Q suivant :
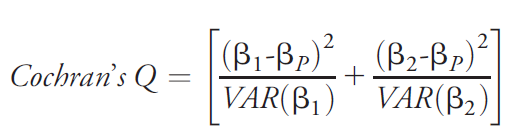
Dans cette formule, β1 représente le logarithme naturel de RP1 et β2 représente le logarithme naturel de RP2 et VAR représente la variance. βp représente le logarithme naturel de RPp qui est l’effet pour les deux groupes ensemble. Une fois que cet estimé Cochran Q est calculé, il suffit de mener un test de χ2 (Kaufman et MacLehose 2013) avec un nombre de degrés de liberté égal au nombre de strates moins un.
Ainsi, si RP1 représente l’effet de l’intervention sur le premier quintile de l’indice de richesse (le plus pauvre) et RP2 l’effet de l’intervention sur le cinquième quintile (le plus riche), et RPp pour les deux groupes ensemble, on estimera que l’intervention est équitable si : i) il y a présence d’un effet hétérogène de l’implantation de l’exemption des frais de soins sur l’accès aux soins obstétricaux et ii) cet effet est plus important pour le premier quintile que pour le cinquième.
Nous avons présenté une approche très simple pour évaluer une potentielle hétérogénéité dans les bénéfices d’une intervention. Cette approche peut être étendue à la prise en compte de facteurs de confusion mesurés dans un contexte d’évaluation des effets d’une intervention. Pour cela, il sera possible de mener, par exemple, des analyses d’appariement (c’est-à-dire le fait de comparer des individus traités et non traités ayant des caractéristiques observables similaires) en utilisant un score de propension (Shadish, Luellen et al. 2006). Une fois le score de propension estimé et l’appariement effectué (détails non discutés dans ce chapitre), il sera possible de mener la même approche d’évaluation de l’hétérogénéité via le Cochran Q test.
Cependant, dans un contexte non expérimental, il est souvent préférable d’avoir recours à des approches de type quasi-expérimental qui sont présentées en détail dans le chapitre précédent, afin d’évaluer les effets d’une intervention. Dans la section suivante, nous proposons différentes approches permettant d’évaluer l’hétérogénéité des effets d’une intervention en utilisant des méthodes quasi-expérimentales.
Approches quasi-expérimentales
L’utilisation des méthodes quasi-expérimentales s’est largement développée ces dernières années en santé publique puisqu’elles présentent des avantages certains du point de vue de l’inférence causale : elles permettent la prise en compte de facteurs de confusion non mesurés. Cette prise en compte peut parfois avoir une importance considérable en comparaison avec les approches de type avant/après, allant jusqu’à modifier la direction de l’association représentant l’effet d’une exposition (Grabich, Robinson et al. 2015). Il existe plusieurs méthodes, par exemple la méthode dite de différence dans les différences (DD) et l’approche de discontinuité dans la régression qui est un cas particulier d’analyse de variable instrumentale, toutes deux présentées dans le chapitre précédent. Ici nous allons nous concentrer sur l’approche de type DD.
Hormis l’évaluation des effets sur une population dans son ensemble (Benach, Malmusi et al. 2011) ou sur un sous-groupe de la population comme les femmes, l’évaluation de l’équité via l’utilisation de méthodes quasi-expérimentales demeure rare. Ici, nous proposons trois approches distinctes permettant d’évaluer l’hétérogénéité dans la distribution des effets d’une intervention avec l’exemple de l’approche DD. Pour illustrer, de manière délibérément simplifiée, comment serait organisée l’évaluation de l’exemption du paiement des frais de soins sur l’accès aux soins obstétricaux en utilisant une approche de type DD, nous pouvons considérer la situation suivante. Entre 2000 et 2010, nous mesurons chaque année la prévalence de l’accès aux soins obstétricaux pour des femmes au sein de deux différents pays (pays A et B) similaires. En 2005, le pays A décide d’organiser l’exemption du paiement des frais de soins (exemption de la tarification des accouchements) tandis que le pays B continue d’appliquer des frais pour les accouchements. On suppose que les pays sont échangeables (voir chapitre précédent pour cet aspect) et que le pays B constitue un contrefactuel valide pour représenter ce qui se serait passé dans le pays A sans la mise en place de l’intervention. L’effet causal de l’intervention sur l’accès aux soins obstétricaux sera mesuré par la comparaison de la différence entre les deux pays après 2005 avec la différence entre les deux pays avant 2005. Nous rappelons que cet effet est mesuré dans les modèles de régression par un terme d’interaction entre une variable qui indique la période post-intervention et une variable qui indique le pays avec intervention (Dimick et Ryan 2014). Pour évaluer la répartition des effets entre différents sous-groupes, nous considérons les quintiles de l’indice de richesse.
Analyses stratifiées combinées à un test d’hétérogénéité.
Une première approche consisterait à mener l’analyse de type DD séparément pour les femmes appartenant au premier quintile de richesse et pour les femmes du cinquième quintile. On obtiendrait deux estimations DD de l’effet de l’intervention : une pour les femmes les plus pauvres et une pour les femmes les plus riches. Ensuite, il suffit de mener un test d’hétérogénéité (tel que décrit précédemment) pour évaluer si l’effet de l’intervention sur l’accès aux soins obstétricaux est hétérogène entre les deux groupes[3]. Si cet effet est hétérogène entre les groupes, d’une part, et que, d’autre part, il est plus important au sein du premier quintile de richesse, alors il sera possible de conclure que la répartition des bénéfices de cette intervention est équitable
Analyses avec double interaction ou analyses de type différences dans les différences dans les différences (DDD)
Une deuxième approche consisterait à évaluer une double interaction. Tel que rappelé précédemment, l’estimation de l’effet d’une intervention via une analyse de type DD se fait au travers d’un terme d’interaction. Ici, il s’agirait d’évaluer la présence d’une double interaction du terme DD avec un indicateur du quintile de richesse. Dit autrement, il s’agit d’évaluer sur le terme DD varie en fonction du niveau de richesse. Ici, l’équité sera évaluée par la significativité de cette interaction et sa direction. Dans notre exemple, comme le premier quintile représente le niveau de richesse le plus bas, ce terme d’interaction doit être négatif pour que la répartition des bénéfices de cette intervention soit jugée comme équitable. Cette approche peut s’apparenter à une analyse de différences dans les différences dans les différences (DDD). Il est possible de trouver des exemples de cette approche dans les écrits en santé publique, avec une approche individuelle (Harper, Strumpf et al. 2014) ou une approche mixée à des analyses de séries temporelles (Benmarhnia, Bailey Z et al. 2016).
Analyses avec méthodes de décomposition
Dans la section précédente ont été présentées différentes mesures d’inégalités, allant des approches simples comparant deux groupes, aux approches comparant plusieurs groupes (ordonnés ou non) comme l’indice de concentration par exemple.
Les méthodes de décomposition ont été développées dans le champ de l’économétrie et initialement utilisées pour expliquer, par exemple, les écarts de revenus selon le sexe (par exemple selon l’âge, le secteur d’activité, le niveau d’expérience). Ces méthodes peuvent être appliquées à la comparaison entre deux groupes où la méthode dite d’Oaxaca Blinder (Oaxaca 1973; O’Donnell et Wagstaff 2008) pourra être utilisée. Ces méthodes peuvent également être appliquées à des mesures d’inégalités plus avancées comme l’indice de concentration (O’Donnell et Wagstaff 2008) tel que discuté plus haut.
Toutefois, leur application à l’évaluation des effets et au travers des méthodes quasi-expérimentales demeure rare également. Ici, nous allons décrire simplement comment appliquer ces méthodes de décomposition à une analyse de type DD.
Les méthodes de décomposition consistent à modéliser quelle serait la diminution des inégalités entre deux ou plusieurs groupes si des expositions étaient ramenées à des niveaux équivalents. Ainsi, dans notre contexte, il suffira de mener des analyses de décomposition entre deux ou plusieurs groupes de richesse par exemple et d’analyser particulièrement le terme d’interaction DD. L’interprétation de ce terme à l’issue de l’analyse de décomposition indiquera si les bénéfices de l’intervention contribuent à réduire les écarts entre les groupes de richesse ainsi que l’amplitude et la direction de cette réduction, ce qui permettra d’évaluer si la répartition des bénéfices de cette intervention peut être jugée comme équitable.
Conclusion
Dans ce chapitre, nous avons présenté la notion d’équité en santé publique, ainsi que plusieurs méthodes pour mesurer les inégalités de santé et différentes approches pour évaluer l’hétérogénéité des effets d’une politique publique. Il est important d’avoir à disposition plusieurs approches méthodologiques correspondant à différentes situations de recherche, où l’on pourra par exemple être intéressé parfois par la comparaison entre deux groupes ou par la compréhension d’un gradient social vis-à-vis d’un indicateur de santé. Chacune des méthodes proposées peut s’inscrire dans différentes approches de santé publique (Benach, Malmusi et al. 2011; Benach, Malmusi et al. 2013) quant à la manière d’aborder une intervention de santé publique, que ce soit via des approches populationnelles ou des approches à universalisme proportionné notamment.
L’évaluation de l’équité en santé publique est importante pour s’assurer que, d’une part, des interventions ne contribuent pas à augmenter les inégalités de santé lorsqu’il s’agit d’approches populationnelles, et, d’autre part, qu’elles répondent aux objectifs énoncés dans le cadre d’interventions visant à réduire les inégalités de santé, notamment en permettant que les bénéfices soient plus importants au sein des sous-groupes ou territoires qui sont identifiés comme les plus vulnérables ou dont les besoins sont les plus importants.
Naturellement, cette évaluation n’est qu’une étape parmi d’autres dans la compréhension de la distribution des effets d’une politique publique et des inégalités de santé plus généralement. Avant toute évaluation de l’équité, il est nécessaire de bien connaitre le contexte d’intervention afin de formuler clairement des hypothèses du point de vue de l’hétérogénéité des effets d’une politique publique. Ensuite, il est également important d’étudier les mécanismes qui entrent en jeu dans la variabilité des bénéfices des interventions de santé publique, afin de maintien (?), à la modification de politiques existantes et la formulation d’expérimentations visant la réduction des inégalités de santé.
Références clés
O’Donnell, O. A. et A. Wagstaff (2008). Analyzing health equity using household survey data: a guide to techniques and their implementation, World Bank Publications.
Cet ouvrage en libre accès (https://openknowledge.worldbank.org/handle/10986/6896) est un excellent moyen de découvrir les différentes approches de mesures des inégalités de santé, ainsi que les méthodes permettant de comprendre les déterminants de ces inégalités et de leurs changements au cours du temps, notamment en lien avec une intervention spécifique.
Harper, S., N. B. King, S. C. Meersman, M. E. Reichman, N. Breen and J. Lynch (2010). Implicit value judgments in the measurement of health inequalities. Milbank Quarterly 88(1): 4-29.
Cet article est incontournable au sein de la littérature des inégalités de santé dans la mesure où, au fil de plusieurs exemples, il met en évidence l’importance du choix de la méthode de mesure des inégalités sur les conclusions. Il détaille également les valeurs implicites qui peuvent guider le choix de certaines méthodes plutôt que d’autres.
Benach, J., D. Malmusi, Y. Yasui, J. M. Martínez and C. Muntaner (2011). « Beyond Rose’s strategies: a typology of scenarios of policy impact on population health and health inequalities. » International Journal of Health Services 41(1): 1-9.
Cet article propose de résumer les différentes approches permettant de structurer des interventions en santé publique, avec une perspective historique intéressante et une évaluation systématique des impacts de chacune de ces approches sur les inégalités de santé.
Références
Althabe, F., Bergel, E., Cafferata, M. L., Gibbons, L., Ciapponi, A., Alemán, A., … et Palacios, A. R. (2008). Strategies for improving the quality of health care in maternal and child health in low‐and middle‐income countries: an overview of systematic reviews. Paediatric and perinatal epidemiology, 22(Suppl. 1), 42-60.
Benach, J., Malmusi, D., Yasui, Y. et Martínez, J. M. (2013). A new typology of policies to tackle health inequalities and scenarios of impact based on Rose’s population approach. Journal of epidemiology and community health, 67(3), 286-291.
Benach, J., Malmusi, D., Yasui, Y., Martínez, J. M. et Muntaner, C. (2011). Beyond Rose’s strategies: a typology of scenarios of policy impact on population health and health inequalities. International Journal of Health Services, 41(1), 1-9.
Benmarhnia, T., Bailey, Z., Auger, N., Kaiser, D., King, N. et K. JS. (2016). A difference-in-differences approach to assess the effect of a heat action plan on mortality and equity in Montreal, Quebec. Environmental Health Perspectives, 124(11), 1694-1699.
Benmarhnia, T., Grenier, P., Brand, A., Fournier, M., Deguen, S. et Smargiassi, A. (2015). Quantifying vulnerability to extreme heat in time series analyses: a novel approach applied to neighborhood social disparities under climate change. International Journal of Environmental Research and Public Health, 12(9), 11869-11879.
Benmarhnia, T., Rey, L., Cartier, Y., Clary, C. M., Deguen, S. et Brousselle, A. (2014). Addressing equity in interventions to reduce air pollution in urban areas: a systematic review. International journal of public health, 59(6), 933-944.
Blas, E. et Kurup, A. S. (2010). Equity, social determinants and public health programmes. Geneva: World Health Organization.
Braveman, P. et Gruskin, S. (2003). Defining equity in health. Journal of epidemiology and community health, 57(4), 254-258.
Braveman, P. A., Cubbin, C., Egerter, S., Chideya, S., Marchi, K. S., Metzler, M. et Posner, S. (2005). Socioeconomic status in health research: one size does not fit all. Jama, 294(22), 2879-2888.
Brown, T., Platt, S. et Amos, A. (2014). Equity impact of interventions and policies to reduce smoking in youth: systematic review. Tobacco control, 23(e2), e98-e105.
Brown, T., Platt, S. et Amos, A. (2014). Equity impact of population-level interventions and policies to reduce smoking in adults: a systematic review. Drug and alcohol dependence, 138, 7-16.
Cartier, Y., Benmarhnia, T. et Brousselle, A. (2015). Tool for assessing health and equity impacts of interventions modifying air quality in urban environments. Evaluation and program planning, 53, 1-9.
Daniels, N. (2006). Equity and population health: toward a broader bioethics agenda. Hastings Center Report, 36(4), 22-35.
Dimick, J. B. et Ryan, A. M. (2014). Methods for evaluating changes in health care policy: the difference-in-differences approach. Jama, 312(22), 2401-2402.
Dzakpasu, S., Powell-Jackson, T. et Campbell, O. M. (2013). Impact of user fees on maternal health service utilization and related health outcomes: a systematic review. Health policy and planning, 29(2), 137-150.
Ellis, R. P. (1987). The revenue generating potential of user fees in Kenyan government health facilities. Social science et medicine, 25(9), 995-1002.
Farrelly, M. C., Nonnemaker, J. M., Chou, R., Hyland, A., Peterson, K. et Bauer, U. E. (2005). Changes in hospitality workers’ exposure to secondhand smoke following the implementation of New York’s smoke-free law. Tobacco Control, 14(4), 236-241.
Filmer, D. et Pritchett, L. (1999). The effect of household wealth on educational attainment: evidence from 35 countries. Population and development review, 25(1), 85-120.
Frazer, K., Callinan, J. E., McHugh, J., van Baarsel, S., Clarke, A., Doherty, K. et Kelleher, C. (2016). Legislative smoking bans for reducing harms from secondhand smoke exposure, smoking prevalence and tobacco consumption. Cochrane Database of Systematic Reviews, (2), p.-p.
Gilman, S. E., Rende, R., Boergers, J., Abrams, D. B., Buka, S. L., Clark, M. A., … et Lipsitt, L. P. (2009). Parental smoking and adolescent smoking initiation: an intergenerational perspective on tobacco control. Pediatrics, 123(2), e274-e281.
Grabich, S. C., Robinson, W. R., Engel, S. M., Konrad, C. E., Richardson, D. B. et Horney, J. A. (2015). County-level hurricane exposure and birth rates: application of difference-in-differences analysis for confounding control. Emerging themes in epidemiology, 12(1), 1.
Hajizadeh, M., Campbell, M. K. et Sarma, S. (2014). Socioeconomic inequalities in adult obesity risk in Canada: trends and decomposition analyses. The European Journal of Health Economics, 15(2), 203-221.
Harper, S., King, N. B., Meersman, S. C., Reichman, M. E., Breen, N. et Lynch, J. (2010). Implicit value judgments in the measurement of health inequalities. The Milbank Quarterly, 88(1), 4-29.
Harper, S., Lynch, J., Meersman, S. C., Breen, N., Davis, W. W. et Reichman, M. E. (2008). An overview of methods for monitoring social disparities in cancer with an example using trends in lung cancer incidence by area-socioeconomic position and race-ethnicity, 1992–2004. American journal of epidemiology, 167(8), 889-899.
Harper, S., Strumpf, E. C., Burris, S., Smith, G. D. et Lynch, J. (2014). The effect of mandatory seat belt laws on seat belt use by socioeconomic position. Journal of policy analysis and management, 33(1), 141-161.
Hoffman, S. J. et Tan, C. (2015). Overview of systematic reviews on the health-related effects of government tobacco control policies. BMC public health, 15(1), 744-754.
Hosseinpoor, A. R., Van Doorslaer, E., Speybroeck, N., Naghavi, M., Mohammad, K., Majdzadeh, R., … et Vega, J. (2006). Decomposing socioeconomic inequality in infant mortality in Iran. International journal of epidemiology, 35(5), 1211-1219.
Houweling, T. A., Kunst, A. E., Huisman, M. et Mackenbach, J. P. (2007). Using relative and absolute measures for monitoring health inequalities: experiences from cross-national analyses on maternal and child health. International journal for equity in health, 6(1), 1.
Howe, L. D., Hargreaves, J. R., Gabrysch, S. et Huttly, S. R. (2009). Is the wealth index a proxy for consumption expenditure? A systematic review. Journal of epidemiology and community health, 63(11), 871-877.
Kakwani, N., Wagstaff, A. et Van Doorslaer, E. (1997). Socioeconomic inequalities in health: measurement, computation, and statistical inference. Journal of econometrics, 77(1), 87-103.
Kaufman, J. S. et MacLehose, R. F. (2013). Which of these things is not like the others?. Cancer, 119(24), 4216-4222.
Kawachi, I. et Kennedy, B. P. (1997). The relationship of income inequality to mortality: does the choice of indicator matter?. Social science et medicine, 45(7), 1121-1127.
Kawachi, I., Subramanian, S. et Almeida-Filho, N. (2002). A glossary for health inequalities. Journal of epidemiology and community health, 56(9), 647-652.
Lagarde, M. et Palmer, N. (2008). The impact of user fees on health service utilization in low-and middle-income countries: how strong is the evidence?. Bulletin of the World Health Organization, 86(11), 839-848C.
Litvack, J. I. et Bodart. C. (1993). User fees plus quality equals improved access to health care: results of a field experiment in Cameroon. Social science et medicine, 37(3), 369-383.
Lynch, J., Smith, G. D., Harper, S. et Bainbridge, K. (2006). Explaining the social gradient in coronary heart disease: comparing relative and absolute risk approaches. Journal of epidemiology and community health, 60(5), 436-441.
Mackenbach, J. P. et Kunst, A. E. (1997). Measuring the magnitude of socio-economic inequalities in health: an overview of available measures illustrated with two examples from Europe. Social science et medicine, 44(6), 757-771.
Marmot, M., Friel, S., Bell, R., Houweling, T. A., Taylor, S. et Commission on Social Determinants of Health. (2008). Closing the gap in a generation: health equity through action on the social determinants of health. The Lancet, 372(9650), 1661-1669.
McKinnon, B., Harper, S. et Kaufman, J. S. (2015). Who benefits from removing user fees for facility-based delivery services? Evidence on socioeconomic differences from Ghana, Senegal and Sierra Leone. Social Science et Medicine, 135, 117-123.
McKinnon, B., Harper, S., Kaufman, J. S. et Bergevin, Y. (2014). Removing user fees for facility-based delivery services: a difference-in-differences evaluation from ten sub-Saharan African countries. Health policy and planning, 30(4), 432-441.
O’Donnell, O. A. et Wagstaff, A. (2008). Analyzing health equity using household survey data: a guide to techniques and their implementation. Washington D.C.: World Bank Publications.
Oaxaca, R. (1973). Male-female wage differentials in urban labor markets. International economic review, 693-709.
Pamuk, E. R. (1985). Social class inequality in mortality from 1921 to 1972 in England and Wales. Population studies, 39(1), 17-31.
Pearcy, J. N. et Keppel, K. G. (2002). A summary measure of health disparity. Public health reports, 117(3), 273-280.
Regidor, E. (2004). Measures of health inequalities: part 2. Journal of epidemiology and community health, 58(11), 900-903.
Ridde, V. et Morestin, F. (2011). A scoping review of the literature on the abolition of user fees in health care services in Africa. Health policy and planning, 26(1), 1-11.
Russell, S. et Gilson, L. (1997). User fee policies to promote health service access for the poor: a wolf in sheep’s clothing?. International Journal of Health Services, 27(2), 359-379.
Say, L. et Raine, R. (2007). A systematic review of inequalities in the use of maternal health care in developing countries: examining the scale of the problem and the importance of context. Bulletin of the World Health Organization, 85(10), 812-819.
Shadish, W. R., Luellen, J. K. et Clark, M. (2006). Propensity scores and quasi-experiments: A testimony to the practical side of lee sechrest.
Smith, M. J. (2015). Health equity in public health: Clarifying our commitment. Public Health Ethics, 8(2), 173-184.
Starfield, B. (2007). Pathways of influence on equity in health. Social Science et Medicine, 64(7), 1355-1362.
Theil, H. (1967). Economics and information theory.
Wagstaff, A., Van Doorslaer, E. et Paci, P. (1991). On the measurement of horizontal inequity in the delivery of health care. Journal of health economics, 10(2), 169-205.
Wagstaff, A., Van Doorslaer, E. et Watanabe, N. (2003). On decomposing the causes of health sector inequalities with an application to malnutrition inequalities in Vietnam. Journal of econometrics, 112(1), 207-223.
Whitehead, M. (1992). The concepts and principles of equity and health. International journal of health services, 22(3), 429-445.
Yates, R. (2009). Universal health care and the removal of user fees. The Lancet, 373(9680), 2078-2081.
Yoder, R. A. (1989). Are people willing and able to pay for health services? Social science et medicine, 29(1), 35-42.
Résumé / Abstract / Resumen
L’équité en santé est largement identifiée comme un objectif auquel les politiques et activités de santé publique doivent répondre en priorité, mais dont la définition varie considérablement. Dans ce chapitre, nous proposons une définition de l’équité en santé qui fait référence à la distribution des bénéfices des politiques publiques. Dans ce chapitre nous présentons différentes méthodes de mesures des inégalités de santé, leur application à l’évaluation des effets des interventions à travers l’exemple de l’effet de l’exemption du paiement des frais de soins sur l’accès aux soins obstétricaux dans le cadre d’un exemple simulé. Ces mesures incluent notamment l’indice de concentration et l’indice de Theil. Enfin, nous proposons différentes approches pour les appliquer à l’évaluation des effets des interventions donc à l’équité incluant une approche simple et une base sur l’utilisation de méthodes quasi-expérimentales. L’évaluation de l’équité en santé publique est importante pour s’assurer que, d’une part, des interventions ne contribuent pas à augmenter les inégalités de santé et qu’elles répondent aux objectifs énoncés dans le cadre d’interventions visant à réduire les inégalités de santé.
***
Health equity is considered a priority for public health interventions and policies, but the concept of an equitable intervention varies in definition. We define an equitable intervention as one that has heterogeneity in its effects, and provides greater benefits for subgroups or territories of a population that have been defined as vulnerable. In this chapter, we assess the impact of an intervention establishing free obstetric care (childbirth costs excluded) on increasing equity and access to care. We notably present the concentration index and the Theil Index. Simulated data from population surveys is used to discuss important issues regarding measurement of inequalities and different indicators that can be used in evaluating the equitability of an intervention. Lastly, two evaluation strategies are discussed: a simple evaluation approach to illustrate the application of inequality measurement methods and an approach based on quasi-experimental designs. These tools to assess public health equity is important to ensure that interventions meet objectives to reduce inequalities and prevent them from contributing to increasing health disparities.
***
La equidad en salud es ampliamente identificada como un objetivo al que las políticas y actividades de salud pública deben responder como una prioridad, pero cuya definición varía considerablemente. En este capítulo proponemos una definición de equidad en salud que se refiere a la distribución de los beneficios de las políticas públicas. En este capítulo se presentan diferentes métodos para medir las desigualdades en salud, su aplicación a la evaluación de los efectos de las intervenciones a través del ejemplo del efecto de la exención de las tasas de atención sanitaria sobre el acceso a la atención obstétrica en un ejemplo simulado. Estas medidas incluyen el índice de concentración y el índice de Theil. Finalmente, proponemos diferentes enfoques para aplicarlos a la evaluación de los efectos de las intervenciones y, por lo tanto, a la equidad, incluyendo un enfoque simple y una base sobre el uso de métodos cuasi-experimentales. La evaluación de la equidad en salud pública es importante para garantizar que, por una parte, las intervenciones no contribuyan a aumentar las desigualdades en salud y, por otra parte, que cumplan los objetivos establecidos en las intervenciones para reducir las desigualdades en salud.
***
Tarik Benmarhnia est Professeur assistant d’épidémiologie à l’Université de Californie à San Diego au sein de l’Institut d’océanographie Scrippset de l’école de médecine. Il a complété son doctorat en épidémiologie à l’Université de Montréal et à l’Université Paris Sud. Il est également chercheur associé au Chili et en France et membre du comité éditorial de Environmental Health Perspectives. Sa recherche porte sur les impacts des évènements extrêmes sur la santé avec un focus sur les populations vulnérables et les implications en termes de politiques publiques. Il développe également des approches méthodologiques pour évaluer l’effet des politiques environnementales sur la santé comme les mesures d’adaptation aux changements climatiques et les mesures de contrôle de la pollution atmosphérique.
Britt McKinnon est chercheuse au centre de Santé mondiale à l’hôpital des Enfants malades et professeure assistante à l’École de santé publique Dalla Lana de l’Université de Toronto. Elle a obtenu son doctorat en épidémiologie à l’université McGill et fait un postdoctorat au sein de L’Institut des politiques sociales et de Santé de McGill. Sa recherche se concentre en en santé mondiale sur la santé maternelle et des enfants, en épidémiologie sociale et l’évaluation des politiques publiques et programmes en santé.
Citation
Tarik Benmarhnia et Britt McKinnon. (2019). Les mesures de l’équité. Un exemple d’intervention de gratuité des soins obstétricaux. In Évaluation des interventions de santé mondiale. Méthodes avancées. Sous la direction de Valéry Ridde et Christian Dagenais, pp. 283-309. Québec : Éditions science et bien commun et Marseille : IRD Éditions.
- Pour plus d’information, voir Kakwani, Wagstaff et al. (1997) et O'Donnell et Wagstaff (2008). ↵
- Pour plus d’informations sur les analyses de décomposition de l’indice de concentration, voir Wagstaff, Van Doorslaer et al. (1991), Wagstaff, Van Doorslaer et al. 2003 et O'Donnell and Wagstaff (2008). ↵
- Ce test peut être mené sur plusieurs groupes également, à condition d’adapter le Cochran Q test. ↵

