La recherche en mathématiques a actuellement atteint un niveau incroyablement élevé pour le commun des humains que la diversité des résultats obtenus, les théories, les concepts. Bref, le vocabulaire mathématique a fait l’objet de dictionnaires issus de différentes collections. L’Encyclopædia Universalis « se veut ainsi le reflet du foisonnement et de l’enchevêtrement de diverses disciplines mathématiques » (Dictionnaire des mathématiques, 1997 : 8). La notion d’interdisciplinarité est vivante dans le domaine des mathématiques. « Comme le soulignait souvent Jean Dieudonné, c’est cette interdisciplinarité interne qui fait la force et l’originalité des mathématiques contemporaines. » (Dictionnaire des mathématiques, 1997 : ibid.). Dans leur développement, les mathématiques se sont ouvertes aux autres disciplines à travers des interactions dont le mode opératoire et le mécanisme fonctionnel sont singuliers pour chaque domaine (Greenwald & Thomley, 2012).

Principe d’adaptation du modèle mathématique avec le monde réel

Des interactions existent entre les ramifications des différentes branches des mathématiques et entre les mathématiques et les autres disciplines. Dans le second cas de figure qui est plus observable aujourd’hui, les chercheur·e·s travaillant dans les autres disciplines étudient ce que Descartes appelle le « monde réel »; celui-ci, par essence, est opposé au monde mathématique qui, lui, est intelligible et est fait majoritairement de notions abstraites comme les angles, les fonctions, les points, les nombres… Hurley (1980 : 493-495) consacre quelques pages aux interactions entre les mathématiques et les autres disciplines. Selon lui, les chercheur·e·s désirent établir, dans leur domaine de travail, des lois qui puissent expliquer ou régir les informations et les données qu’ils récoltent lors de leurs travaux, réalisés dans le monde réel. De telles lois prennent la forme d’énoncés mathématiques (équations, théorèmes, formules, propriétés, règles) relativement à un modèle mathématique conséquent avec des paramètres reflétant, dans la mesure du possible, le phénomène réel étudié : son mécanisme de fonctionnement, sa dynamique dans l’espace et dans le temps, entre autres. Ce modèle est souvent un système mathématique abstrait contenant, autant que faire se peut, toutes les variables essentielles existant dans l’arrière-plan (Hurley, 1980).

Ensuite, par un travail purement mathématique sur ce modèle, les mathématiciens et les mathématiciennes peuvent obtenir des résultats à condition qu’ils/elles disposent des outils adéquats pour y parvenir. L’interprétation de ces résultats, dans le monde réel, peut permettre de faire des prédictions sur le comportement ultérieur du phénomène. La comparaison de ces prémonitions avec les résultats empiriques permet de mesurer alors le degré avec lequel le modèle mathématique capte l’essence de la situation réelle du phénomène étudié. Selon Hurley (1980), deux cas de figure se présentent :

Si les prédictions correspondent presque parfaitement aux résultats expérimentaux, alors le modèle sera adopté et ses résultats seront appelés lois^[1] du champ externe. Si les prévisions sont faiblement corrélées avec les résultats expérimentaux, alors un modèle révisé ou affiné peut être construit, sous réserve peut-être d’être encore affiné après une nouvelle expérimentation^[2]. (Hurley, 1980 : 394)

Ainsi, si les résultats prévisionnels sont en corrélation parfaite avec les résultats expérimentaux, alors ce modèle mathématique sera adopté par les chercheurs et les chercheuses de la discipline concernée. Dans le cas où la corrélation entre les deux types de résultats est faible, un autre modèle plus élaboré et plus fin doit être construit en multipliant davantage les expériences.

Hurley (1980) résume les deux situations à travers le schéma ci-après.

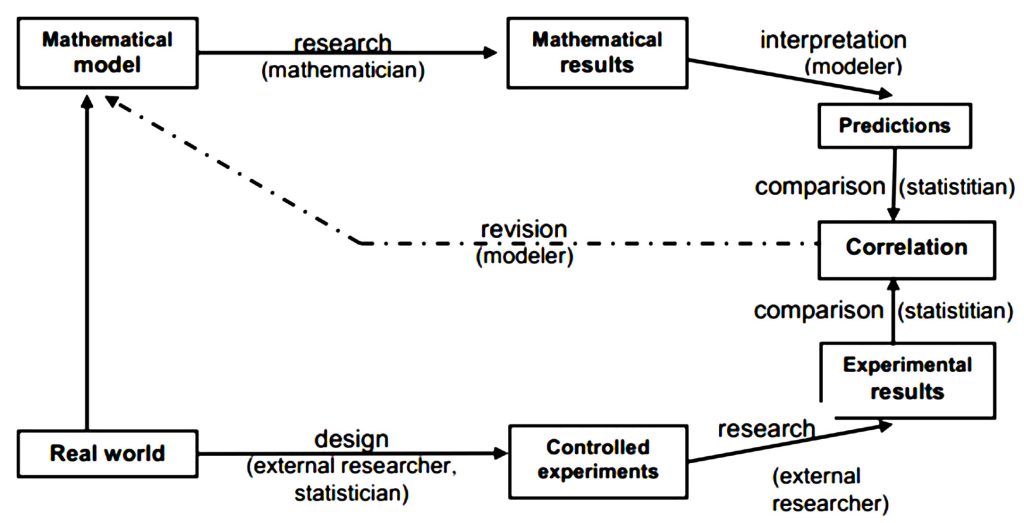
Cette représentation schématique présente un intérêt capital pour la MCA dans la mesure où elle établit des liens solides entre le modèle mathématique et le monde réel. Cependant, un aspect semble être écarté par Hurley. L’idée qu’une faible adéquation entre les résultats du modèle et la réalité peut conduire à une compréhension erronée selon laquelle l’élaboration et la prolifération des théories se font de manière isolée. Or, il faut appréhender ces relations en termes de perfectionnement, d’amélioration, d’effacement des « lacunes » du modèle (Khun, 1972). Nous pensons donc qu’il faut insister sur les liens, les filiations épistémologiques entre différents théories et modèles. Sans cet aspect, on perdrait une part importante d’informations sur la construction des connaissances et le développement cognitif : les savoirs mathématiques ne naissent pas d’eux-mêmes, ce sont des constructions de l’esprit humain. Il convient également de présenter avec précision les éléments qui entrent en jeu dans les interactions, notamment le monde réel, dans lequel les observations du phénomène étudié sont faites, et le modèle mathématique, qui relève du monde intelligible. Le modèle mathématique étant construit à partir des informations issues du phénomène du monde réel, il serait plus intéressant de disposer en interaction, d’une part, les deux ensembles (monde réel et monde intelligible); et d’autre part, les objets appartenant à chacun des deux ensembles (phénomène réel et modèle mathématique). De plus, le schéma de Hurley (1980) nous laisse visiblement dans une impasse lorsqu’il y a corrélation parfaite entre les prédictions et les résultats expérimentaux. Il serait important d’indiquer un emplacement (cadre) qui montre le résultat (modèle) final qui fera office de loi dans le domaine réel. Il convient de remarquer qu’ici, le développement des modèles mathématiques a créé un meilleur cadre de réflexion qui, à son tour, a permis la synthétisation des lois, leur regroupement et la trouvaille d’une certaine unité entre elles.

Par ailleurs, l’inadéquation entre le modèle mathématique et le monde réel ne se résout pas toujours par l’édification de nouveaux modèles mathématiques. En effet, on peut partir de la mise en pratique des paramètres du modèle en réexaminant leur fonctionnement dans le monde réel. Le cheminement pourrait donc être représenté sous la forme d’une bifurcation qui a pour point de départ le monde réel, puis l’élaboration du modèle mathématique, suivie des résultats obtenus; arrivée à ce niveau, deux chemins se fraient : soit le retour vers le modèle (Hurley, 1980), soit le retour au monde réel. Notre proposition consiste à considérer prioritairement ce dernier chemin. De manière concrète, en recourant à ce chemin, cela nous permet de résoudre des problèmes tels que la mauvaise formulation d’un problème, l’omission d’un paramètre, etc.

En reprenant les grands traits du schéma de Hurley, nous proposons ci-dessous une configuration enrichie de nos propres expériences.

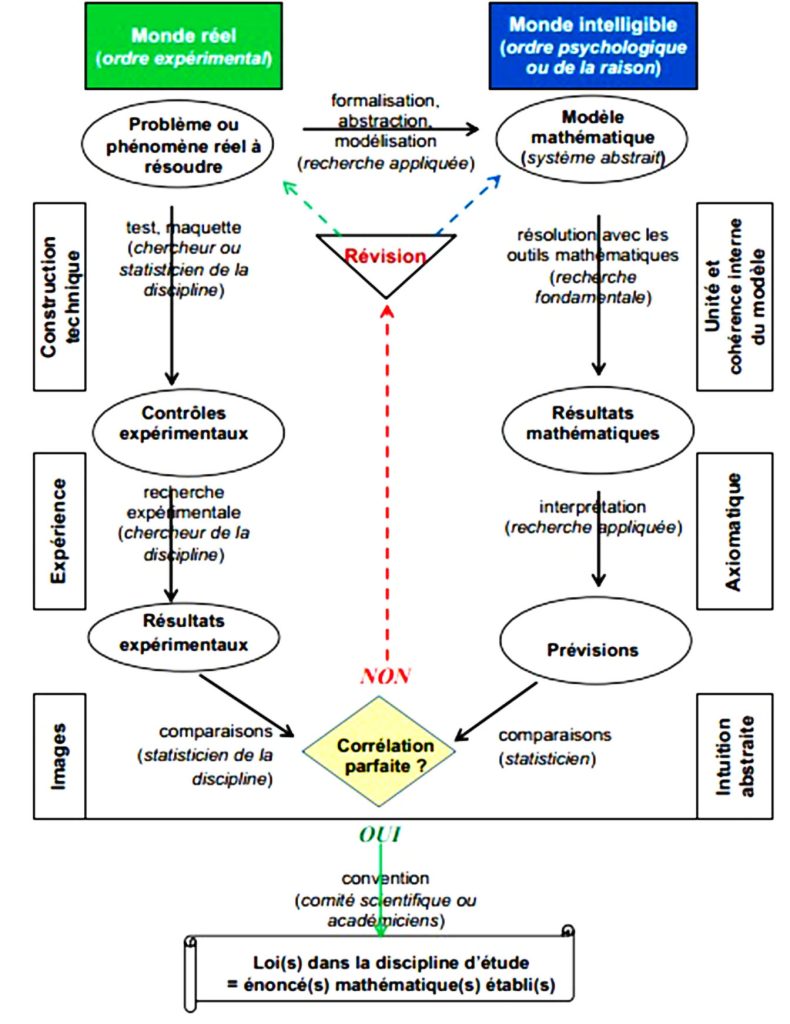
Ce schéma montre que le mécanisme interactionnel est fait d’actions bien planifiées aussi bien dans le monde réel que dans le monde intelligible. Dans le monde réel, on commence par des constructions techniques à travers des tests, puis l’expérience à l’aide des protocoles contrôlés débouchant sur des résultats expérimentaux, et enfin, l’image se crée à travers les comparaisons. Tandis que dans le monde intelligible, on commence par assurer la cohérence et l’unité interne du modèle, puis l’axiomatique aboutit aux prédictions et l’intuition permet de discerner ces prédictions.

Mais il peut arriver que le mathématicien ou la mathématicienne trouve plusieurs modèles relatifs à un même phénomène réel. Le choix du meilleur modèle devient alors crucial. Chaque modèle donne des prédictions sur le comportement du phénomène et nous pouvons nous demander lequel des ensembles de prévisions correspond le mieux à l’expérience menée. Dans certains cas, tel modèle est parfaitement adéquat. Dans d’autres, un autre modèle est préférable. Ainsi, le choix du modèle à utiliser ne dépend plus seulement des facteurs mathématiques, mais également des facteurs environnementaux; bref, des facteurs extérieurs ayant directement des effets sur le phénomène réel étudié.

Processus d’interactions des mathématiques avec d’autres disciplines

En nous inspirant du schéma du processus d’adaptation du modèle mathématique dans les autres disciplines élaboré par Hurley (1980 : 494) et des travaux de Wieruszewski (1994), nous proposons la schématisation suivante, qui à la fois simplifie le processus pour les apprenant·e·s du secondaire tout en l’enrichissant par l’ajout d’opérations à mettre en place.

Le problème réel est d’ordinaire posé dans la langue courante et dans des situations de communication quotidienne. Le problème exprimé en dehors du raisonnement formel semble dépouillé d’un ensemble de contraintes et d’éléments sous-jacents : les non-dits, les implicites, les sous-entendus qui engendrent nécessairement des erreurs et des malentendus^[3]. Il se traduit ensuite en langue mathématique qui doit établir des lois ou des règles permettant de décrire explicitement des faits observables et identifiables. Cette langue qui se différencie des langues naturelles tend donc à effacer certains paramètres susceptibles de connaitre des variations, notamment les paramètres du contexte d’énonciation : le sujet parlant, ses sentiments, le temps, l’espace^[4]. Ensuite, le problème est résolu selon les méthodes et techniques spécifiques. Enfin, les résultats éventuels trouvés sont vérifiés et réinterprétés en langue naturelle.

À titre d’illustration, nous présentons dans le tableau ci-dessous des exemples de rapports analogiques simples qu’on pourrait faire entre une vision philosophique et une vision mathématique de quelques formulations de sujet dans des domaines de recherche ou de travail donnés.

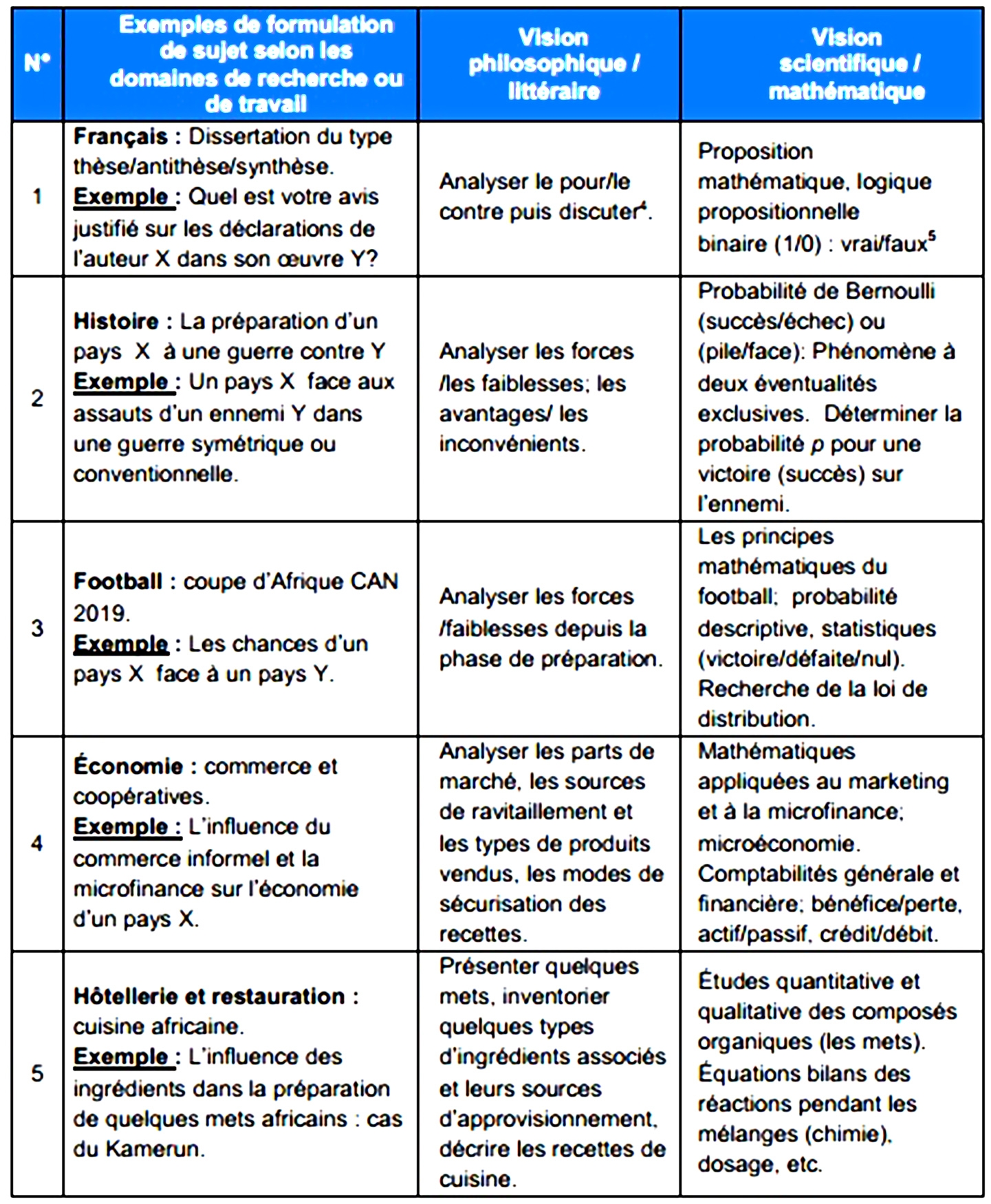
Ce tableau fait ressortir deux manières d’envisager les problèmes et de les résoudre. Il met aussi en évidence les relations entre les mathématiques et les études littéraires. Ceci constitue l’un des enjeux de la MCA qui ambitionne d’appréhender l’apprentissage des mathématiques en corrélation avec les activités humaines. Les exemples foisonnent dans divers secteurs.

Nous rappelons que les mathématiques appliquées traitent du monde réel où les critères absolus (vrai/faux, un/zéro…) qui relèvent des mathématiques fondamentales et notamment de la logique formelle, classique, binaire ou booléenne ne sont plus tout à fait appropriés. Très souvent, aucun modèle n’est absolument correct. Dès lors, il devient plutôt intéressant de savoir et faire savoir lequel parmi les modèles proposés donne la meilleure approximation du comportement observé pendant l’expérience. En outre, les critères deviennent relatifs, de l’ordre de la logique plurivalente ou logique floue (Godjevac, 1999) d’autant plus que dans la réalité humaine, la notion de vérité est plus aléatoire. La logique floue est en effet une extension de la logique classique qui permet alors de modéliser et de simuler des complexités des données de la réalité humaine. Elle se rapproche, dans une certaine mesure, de la flexibilité du raisonnement humain. Elle permet de traiter des variables non exactes dont la valeur peut varier entre 0 et 1. Ses applications sont nombreuses, allant des systèmes de jeux vidéo aux pilotes automatiques en passant par les microondes, la décision du montant du pourboire à l’issue d’un repas au restaurant en fonction de la qualité ressentie du service ou de la qualité de la nourriture (Kono, 2014). Il faut souligner que le problème ne se pose pas seulement en termes de modélisation, mais aussi en termes de simulation de temps de calcul. À ce propos, on pourrait par exemple questionner la qualité d’un modèle métrologique qui ferait des prédictions sur deux jours alors que les calculs en machine prendraient trois jours.

À l’observation, toutes ces expériences montrent l’étendue des relations réciproques qu’entretiennent les mathématiques avec les autres disciplines; des corrélations aussi nombreuses que diverses existent, comme le montrent les exemples que nous allons examiner.

Les mathématiques se révèlent véritablement aujourd’hui comme une science de services, c’est-à-dire une science qui met ses outils à la disposition des autres disciplines. Pourtant, Von Neumann fait observer que la dimension utilitaire des travaux mathématiques n’est pas toujours perceptible immédiatement.