Les propositions évoquées ci-dessus pourraient davantage convaincre la jeunesse à retourner à l’école pour ceux et celles qui ont abandonné leurs études, à s’intéresser aux mathématiques pour ceux et celles qui nourrissent une désaffection à l’égard de cette discipline, à mieux prendre conscience du sérieux qu’elle devrait consacrer à la construction de son avenir, à s’intéresser et s’appliquer davantage dans la pratique et l’expérimentation quotidienne des mathématiques dans toutes ses actions. Par conséquent, nous pouvons reprendre à notre compte, mutatis mutandis, l’assertion de Jaspers à propos du caractère indispensable de la philosophie : « L’homme ne peut se passer de la [mathématique]. Aussi est-elle présente partout et toujours, répandue dans le public… » (1981 [1950] : 10). On la retrouve dans les pratiques marchandes traditionnelles, dans les formules de gestion courante de la fortune et aires culturales, dans les pratiques opératoires conventionnelles. Russell, quant à lui, met en garde toute personne qui aspire à être philosophe  : « celui qui veut devenir philosophe a tout avantage à acquérir une vaste connaissance des mathématiques » (Russell, 2005 : 6); une acquisition de connaissances basée sur une approche historique afin d’être au fait des grandes lignes des théories mathématiques, pour se familiariser avec le raisonnement hypothético-déductif et pour minimiser les erreurs de jugement de tout genre.

Autrement dit, les mathématiques ne sont pas l’apanage d’une catégorie de personnes. Elles constituent toute une culture, une façon de penser opératoire et opérationnelle susceptible d’être reçue par tout le monde à travers les générations. Les mathématiques élémentaires, grâce à leur démarche (réfléchie, logique, systématique…) et quand elles sont débarrassées de leurs signes, symboles et autres figures géométriques, sont donc une activité populaire. Celles-ci n’exigent aucune restriction fondamentale pour ceux et celles qui désirent l’exercer, la pratiquer. Il est aisé de constater que dans l’imagerie populaire le simple fait d’évoquer le mot « mathématique » fait tout de suite penser, dans la plupart des cas, aux signes, aux symboles et aux figures abstrait·e·s; reléguant de ce fait la démarche au second plan. L’idée, ici, c’est d’inverser cet ordre en priorisant la méthode mathématique dont les vertus en matière de rigueur et de cohérence sont reconnues. C’est d’ailleurs là le tremplin pour toute phase d’apprentissage. Des enfants aux adultes, aucun n’échappe aux mathématiques dans la gestion quotidienne de sa vie.

En réalité, la pratique des mathématiques peut être consciente ou inconsciente. C’est le cas de ce jeune qui répare aisément un téléphone portable high-tech sans avoir achevé avec succès ses études de mathématiques et d’informatique du cycle primaire. A contrario, on a également des cas d’intellectuel·le·s et d’ingénieur·e·s de haut niveau qui peuvent raisonner et discourir sur la constitution et le fonctionnement de cet appareil sans en avoir jamais vu l’intérieur. On distingue ainsi, la connaissance de l’appareil et la connaissance sur l’appareil. C’est ce qu’explique le philosophe du langage Auroux quand il prend l’exemple de l’intégrateur. Il fait une distinction entre la connaissance de ce qui se passe dans la machine appelée intégrateur et le discours sur cet intégrateur. Tout en reconnaissant que la connaissance de l’intégrateur est en relation avec le discours sur l’intégrateur, il précise que les deux connaissances n’ont de relation que sur la base de postulat ou d’hypothèse. Ainsi, on peut être en mesure de discourir et de raisonner sur l’intégrateur sans jamais avoir vu l’appareil lui-même : « c’est le cas d’un mathématicien qui n’a jamais vu d’intégrateur! Il pourra en dire quelque chose du genre : toute machine intégratrice devra considérer deux variables, les variations de l’une dépendront de la valeur instantanée de l’autre. » (Auroux, 1992 : 44).

Les mathématiques occupent une place de choix parmi les disciplines scientifiques en ce qu’elles offrent un modèle de recherche empirique ou inférentiel de la vérité scientifique exempte de toute transgression ou contradiction. Avec l’évolution de la recherche, on peut, en tout lieu et en toute circonstance, se demander aujourd’hui où on n’utilise pas les mathématiques? Dans quels secteurs d’activité n’utilise-t-on pas les mathématiques? Cette omniprésence des mathématiques dans la vie des hommes et des femmes contraste avec l’attitude de rejet qui s’observe chez ces mêmes personnes. Un tel paradoxe ne peut s’expliquer que par l’ignorance et les considérations stéréotypées dont les origines se trouvent dans des malentendus qui se sont généralisés au fil du temps. La démarche du pédagogue consisterait ainsi à agir de sorte à modifier ces idées « anti-mathématiques » pour les transformer en des idées favorables à cette discipline. Nous sommes là dans le droit fil de la stratégie de démystification des mathématiques : amener des personnes à reconsidérer leur désamour pour les mathématiques en leur apportant la preuve qu’ils pratiquent les mathématiques. Il est question de trouver les moyens d’agir positivement sur ce que pensent les gens à propos des mathématiques. Il est impératif de faire comprendre à l’opinion que les constructions mathématiques qu’elle pense être coupées de la réalité ont tout à voir avec les préoccupations de Monsieur et Madame Tout-le-Monde qui a faim, qui n’a pas de logement, qui a des problèmes de santé… De manière pratique, cette personne a besoin de réfléchir sur son environnement (géométrie, algèbre), d’offrir ses services (lois de composition, morphismes de structures), obtenir de l’argent et savoir le gérer (théorie keynésienne sur la propension marginale à consommer). Comme on le voit, en écartant tout le travail d’abstraction et en mettant en avant la démarche, on peut facilement faire ressortir la relation entre mathématiques et réalité.

Par ailleurs, les scientifiques en général doivent également se remettre en question et agir prioritairement sur les besoins réels en vue d’améliorer la vie quotidienne des humains. Nous faisons donc un plaidoyer pour des mathématiques au service du développement, des mathématiques mieux contextualisées et plus ancrées dans les cultures humaines. Dans ce sens, Sladek fait une observation assez bouleversante et appelle les scientifiques à plus d’humanisme.

Le problème de la science contemporaine, c’est qu’elle fournit des réponses à toutes les mauvaises questions. Personne ne demande si le laser est oui ou non un faisceau d’énergie cohérente opérant dans les limites du spectre lumineux […]. Personne ne veut savoir si E égale vraiment mC². Il est grand temps que les scientifiques sortent de leur tour d’ivoire, cessent de jouer avec les microprocesseurs ou l’analyse transactionnelle et s’attaquent à quelques-uns des vrais mystères de notre époque. (Sladek, cité par De Pracontal, 1986, leçon 3)

De Pracontal, dans sa posture de journaliste scientifique, s’attaque à deux principaux problèmes que l’on rencontre dans le monde scientifique; le premier étant sa relation avec les préoccupations réelles des citoyen·ne·s. Les résultats des travaux scientifiques sur l’armement, le dopage, le clonage, le problème de Fermat, le problème des corps, etc. constituent-ils les priorités parmi les problèmes humains? Le second problème est cette espèce de barrière qui s’érige entre le scientifique et la société (« tour d’ivoire ») et qui fait penser que le scientifique est un être à part et que son discours, voire ses formules (par exemple E = mC²) ne sont pas sujettes à discussion. Il déplore ainsi le fait que les savants pensent avoir mieux à faire que de s’occuper de nos « petits » problèmes journaliers (logement, santé, alimentation, chômage, drogue, insécurité, terrorisme…). Il convient de rappeler que De Pracontal, titulaire d’une maîtrise de mathématiques et d’un doctorat en sciences de l’information sur la vulgarisation scientifique, n’est pas un journaliste ordinaire. Il s’intéresse surtout à notre manière de traiter l’information pour certain·e·s et de l’accueillir pour d’autres : « Disposons-nous d’un esprit critique face à la masse d’information véhiculée par les médias? Ou sommes-nous à la merci de la société d’information? ». Étant donné que pour les médias et le grand public, l’irrationnel est souvent plus sensationnel que le rationnel, De Pracontal « va tenter de nous faire mieux distinguer le vrai du faux dans cette culture surmédiatisée, régie par ‘la dictature du marché et de l’audimat’. Car il faut l’avouer, pour les médias, il est beaucoup plus intéressant de présenter l’irrationnel et toutes les merveilles qu’il en découle plutôt que la froide rigueur scientifique… » (Utilisateur supprimé, 2004, paragr. 6)^[8].

Pour ce qui concerne les mathématiques, l’insignifiance invraisemblable du degré de corrélation entre les « grands » résultats obtenus en laboratoire et leurs impacts observables sur les « petits » problèmes quotidiens de l’humain sème un doute au sein du grand public et le ramène à une résultante inéluctable : le refus de la science mathématique. Face à cette abondance d’informations et de désinformations sur l’importance des mathématiques pour la société, il convient de faire preuve d’un peu de discernement et surtout de beaucoup de bonne foi.

Dans le cas de l’Afrique, ce décalage entre le monde de la science (écoles, universités, instituts) et la société se trouve exacerbé par des facteurs d’un autre ordre : les croyances, les mythes et les attitudes physico-culturelles.

Sur les facteurs socioculturels : y a-t-il une disposition d’esprit favorable aux mathématiques?

L’histoire ainsi que les recherches démontrent que la différence entre les pays « pauvres » (d’Afrique en particulier) et les pays « riches » (d’Europe par exemple) n’est liée ni à une prédisposition défavorable quelconque ni à la race, encore moins à la couleur de la peau des peuples. Les travaux de Bessone (2013a; 2013b) sur le concept de race montrent que cette notion n’a aucun fondement biologique, mais elle est une construction sociale. De même, Gourou relève que les tests psychologiques utilisés pour montrer les différences d’intelligence « aboutissent toujours, quand les différences sont constatées entre les groupes, à révéler qu’elles sont liées à des conditions sociales. » (1959 : 143). En effet, des citoyen·ne·s d’Afrique considéré·e·s comme paresseux·euses dans leurs pays d’origine deviennent, lorsqu’ils et elles s’installent en toute légalité et dans des conditions favorables (en Afrique ou ailleurs), une puissance productive. Pour s’en convaincre, il suffit de voir les classements réguliers des jeunes entrepreneur·e·s africain·e·s. Dans le classement Forbes Magazine^[9] des 30 jeunes africain·e·s les plus prometteur·euse·s en 2018, on retrouve des Nigérians ayant créé des entreprises dans le domaine du numérique et faisant un chiffre d’affaires annuel de plus de trois millions de dollars, des Sud-africains ayant mis en place des entreprises opérant dans l’énergie solaire ou encore ce Nigérian de 24 ans qui est le plus grand vendeur de voitures dans son pays, etc.

La problématique de l’échec et du décrochage en mathématiques au primaire, au secondaire comme au supérieur suscite toujours, et dans sa complexité, un intérêt sans cesse croissant auprès des scientifiques de l’éducation. La qualité et la quantité des apprentissages dans cette discipline, et partant, des méthodes d’enseignement restent au centre des investigations. Au primaire et au secondaire, l’interdisciplinarité scolaire est une approche prometteuse. Au supérieur, les neuroscientistes affirment que des solutions idoines contre ces fléaux viendraient d’une approche transdisciplinaire qui permettrait de mieux comprendre les apprentissages. La neuroscience des mathématiques est une discipline hybride née d’une posture scientifique et intellectuelle, la transdisciplinarité, qui renvoie à l’interdisciplinarité scientifique, de Lenoir & Sauvé (1998).

Ce concept va au-delà du cloisonnement entre les mathématiques et les neurosciences (la biologie, la génétique, neurologie, médecine…) pour obtenir leur fusion totale. Pour l’OCDE, la transdisciplinarité est ce

concept par lequel des disciplines complètement différentes, fusionnant l’une avec l’autre, donnent naissance à une discipline nouvelle dotée de sa propre structure conceptuelle, qui permet de faire reculer les frontières des sciences et des disciplines ayant présidé à sa formation. (2007 : 275)

À propos des neurosciences, il faut reconnaitre que :

La neuroscience des mathématiques n’en est qu’à ses balbutiements, mais le domaine a beaucoup progressé ces dix dernières années. Les scientifiques ont commencé à mettre au jour des influences biologiques pertinentes – comme l’association entre nombres et espace – et leurs travaux peuvent être nourris par les progrès rapides de la génétique. De plus, les chercheurs commencent seulement à étudier les effets que l’apprentissage des mathématiques a sur le cerveau. Ce sujet doit être étudié d’un point de vue dynamique et développemental, afin que les multiples voies possibles soient définies. (OCDE, 2007 : 111)

Malgré les efforts en matière infrastructurelle et en ressources humaines réalisés par des États africains dans le secteur de l’enseignement aussi bien au niveau public que privé, comment expliquer que le phénomène de l’échec en mathématiques reste toujours perceptible dans certaines structures éducatives pourtant mieux organisées? Les neuroscientistes-mathématicien·ne·s expliquent qu’il existerait chez certains humains un facteur purement biologique qui causerait des entraves à l’apprentissage mathématique, « la dyscalculie ».

Certains enfants ont des difficultés en mathématiques alors que leur formation est suffisante : cela peut être dû à une dyscalculie, l’équivalent mathématique de la dyslexie^[10]. La dyscalculie est un trouble de la perception des nombres, de la compréhension des quantités numériques et de leurs rapports. (Landerl, Bevan et Butterworth, 2004, cités par OCDE, 2007 : 110)

Sans être en contradiction avec notre position selon laquelle les mathématiques se développent mieux à travers des apprentissages contextualisés dans un environnement nourri par une mentalité scientifique, ces résultats viennent renforcer l’idée des mathématiques comme création humaine, fruit d’une éducation culturelle millénaire : « la découverte de caractéristiques neurales atypiques associées à certains troubles mathématiques précis renforce l’idée que les mathématiques n’émergent pas uniquement d’un processus culturel. » (OCDE, 2007 : 110-111). Dès lors, le champ des préalables exigibles aux pratiquant·e·s et praticien·ne·s de cette discipline se voit ainsi augmenté : en plus de disposer et d’entretenir un état d’esprit de nature scientifique ouvert et fécond, il faut prédisposer d’un minimum de « bonne » structuration cérébrale spécifique : « certaines structures cérébrales, qui assurent les fondements conceptuels de l’apprentissage, doivent de plus être intactes et fonctionnelles. » (OCDE, 2007 : 111). Quand cette prédisposition biologique n’est pas naturelle comme chez les enfants précoces ou à haut potentiel en mathématiques (Camos, 2004), elle peut être acquise, pour les autres types d’enfant, par l’adoption d’une hygiène de vie assez spéciale dans un environnement de travail tout aussi spécial couplé à une bonne alimentation^[11]. Cette prédisposition allierait à la fois bien-être physique et intellectuel, aspects émotionnels et cognitifs, esprit analytique et capacités créatrices.

La neuroscience montre que la façon dont on nourrit et traite le cerveau joue un rôle crucial dans les processus d’apprentissage, et commence à déterminer quels sont les environnements les plus favorables à l’apprentissage. La plupart des façons d’améliorer le fonctionnement cérébral dépendent de facteurs simples et quotidiens – qualité de l’environnement social et des rapports humains, alimentation, exercice physique et sommeil – qui semblent tellement évidents qu’on a tendance à négliger leur importance. En prêtant attention à l’état du cerveau et du corps, il est possible de mettre à profit la plasticité cérébrale et de faciliter l’apprentissage. Il faut adopter une approche globale, qui tienne compte des liens étroits entre bien-être physique et intellectuel et ne néglige pas l’interaction entre aspects émotionnels et cognitifs. (OCDE, 2007 : 14)

Il est donc important de reconnaitre qu’en dehors des espèces humaines rares comme les « génies », l’organisation socioculturelle et l’environnement ont un impact significatif sur la construction des capacités mathématiques des apprenant·e·s. Nous pensons que ces dernières ont, de ce fait, des fondements biologiques (et non raciaux !), psychologiques, analytiques et neuroscientifiques. Ici encore, l’enseignant·e peut avoir de l’influence dans cette construction des capacités des apprenant·e·s.

Le récit suivant est un témoignage personnel sur le contexte assez équivoque de l’éducation mathématique en Afrique et la contribution attendue des enseignant·e·s au réveil et à la construction de potentiel mathématique des apprenant·e·s. Cette anecdote est mon histoire.

Pendant tout mon cycle secondaire au lycée mixte de Yokadouma (Est-Kamerun), j’ai toujours été, malgré mon caractère un peu timide, un bon élève sur le double plan de la discipline et du travail. Cependant, en juin 1987 j’ai raté mon Baccalauréat C. Et pour cause : je n’ai pas obtenu une bonne performance en mathématiques. D’ailleurs, je n’ai pas eu de notes au-dessus de la moyenne pendant toute l’année scolaire. C’est ainsi que j’ai repris la terminale l’année scolaire suivante. Heureusement, l’administration nous affecte un nouvel enseignant de mathématiques, Monsieur Tankeu. C’est un jeune enseignant très engagé, un peu effacé, mais un travailleur patenté et rigoureux. En une année scolaire, Monsieur Tankeu, grâce à son approche pédagogique avant-gardiste, assez originale et qui se démarquait visiblement de l’approche par les contenus ou par transmission en vigueur à cette époque, m’a aidé à vaincre mes peurs et à sortir de ma timidité. Il appliquait avec efficacité l’approche par objectifs (APO). Nous travaillions intensément les cours et les exercices d’application en présentiel. Chaque élève avait l’obligation de passer au tableau pour traiter (avec succès ou non) une question dans un exercice ou un exercice entier. Sa gestion de classe créait l’esprit de défi entre les élèves. Il utilisait ces expressions comme un refrain pendant les séances de cours ou d’exercices : « Laissez de côté le superflu! », « Attaquez le problème! », « Qu’est-ce qu’on connait? », « Quelles sont les hypothèses du problème? »,  « Qu’est-ce que tu cherches? », « À quoi ça sert? », etc. Il était si rigoureux qu’il rendait souvent son cours ennuyeux, puisqu’il accordait très peu ou presque pas de temps pour les blagues.

Chaque fin de chapitre était marquée par des exercices ou une recherche à faire à domicile et à remettre une ou deux semaines après, selon leurs degrés de difficultés. La plupart de ces exercices étaient des exercices d’approfondissement tirés des livres de Mathématiques – Terminale C (tomes 1 et 2) des collections Monge et/ou Queysanne-Revuz. Ses évaluations étaient toujours structurées en trois parties : une première partie consacrée aux questions de cours; une deuxième partie portant sur des exercices d’algèbre, d’analyse et/ou de géométrie suivant le niveau progression dans le programme annuel; et une troisième partie constituée d’un problème. C’est ainsi que ma note en mathématiques est passée, d’une année à l’autre, de 05,5/20 à 12,5/20 avec le nouvel enseignant. En juin 1988, je réussis mon Bac avec la mention « Assez bien » et une moyenne (note de l’écrit et note de l’oral) de 14/20 en mathématiques. Je crois pertinemment que j’aurais eu une mention plus élevée si j’avais suivi les cours de cet enseignant deux ou trois années plus tôt.

Pendant l’année scolaire, mon environnement socio-familial n’avait pas connu de changements importants. Je n’ai pas eu de répétiteur. Les seules nouveautés survenues dans mon environnement social étaient mon nouvel enseignant, avec sa méthode d’enseignement et d’évaluation, la discipline en termes de rigueur adoptée dans mon travail à l’école comme à la maison; et il y aussi la gestion stratégique de mes week-ends ponctués par les séances de football que je pratiquais régulièrement; c’était d’ailleurs mon passe-temps préféré. Mais l’histoire ne s’arrête pas là.

Trois mois après, nous sommes au mois d’octobre 1988, période des inscriptions à l’Université de Yaoundé 1, je rencontre Monsieur Tankeu, mon enseignant de maths, en séjour dans la cité capitale. Pendant nos échanges, il me demande la filière que j’ai choisie. Je lui réponds que j’aimerais faire les sciences économiques ou les sciences physiques, mais avec une préférence pour le second choix.

– Non Christophe! répliqua-t-il. Compte tenu de tes performances en mathématiques, tu gagnerais à t’inscrire en mathématiques. Je sors alors ma fiche d’inscription qui n’était pas encore remplie et je coche la filière « mathématiques ».

C’est ainsi que je m’inscris en mathématiques. Trois années plus tard, en juillet 1991, je suis major de ma promotion en licence de mathématiques avec mention « Assez bien ». J’obtiens ensuite une inscription à l’école doctorale dans la même institution et une admission au second cycle de l’école normale supérieure (ENS) de Yaoundé. Deux années plus tard, je sors de l’ENS nanti du diplôme de professeur des lycées d’enseignement général, second grade, option mathématiques. Je pense que Monsieur Tankeu était pour moi, plus qu’un simple enseignant, un conseiller, un guide^[12].

Cette histoire illustre à souhait l’évidence de l’effet de l’enseignant·e, c’est-à-dire l’influence de celui-ci ou de celle-ci sur le destin scolaire des apprenant·e·s en matière d’éducation et d’orientation scolaire et/ou professionnelle. Dans ces deux domaines, cette aptitude à s’intéresser à la vie scolaire des enfants, à diagnostiquer leurs capacités et leur potentiel mathématique, est une « valeur ajoutée » qui, parmi d’autres, semble manquer le plus à nombre d’enseignant·e·s de mathématiques en Afrique. En l’absence d’un module d’éducation à la compréhension en formation initiale dans les écoles normales supérieures, les enseignant·e·s se retrouvent une fois de plus seul·e·s face à cet autre défi professionnel.

De même que la culture mathématique, il faut noter que la culture entrepreneuriale qui ambitionne autant le développement est, elle aussi, plus marquée dans d’autres régions du monde.

En 2009, une enquête Eurobaromètre de la Commission européenne a interrogé l’attitude des citoyens à l’égard du travail indépendant et de la création d’entreprise. Il en ressort, entre autres choses, que 28 % des citoyens interrogés affirment « très/plutôt faisable » de prendre le statut de travailleur indépendant dans les cinq années à venir, chiffre qui reste inférieur toutefois à celui des États-Unis (36 %) ou de la Chine (49 %).

C’est justement au sein des deux cohortes les plus jeunes (15-24 ans et 25-39 ans) que l’optimisme quant à la création d’une entreprise est le plus marquant. (Campy, 2014 : 26)

La différence de perception semble résider fondamentalement dans la mentalité collective, l’attitude acquise par les peuples à travers l’éducation et la culture au cours de l’histoire. Fanon (1961) avait déjà montré comment la colonisation a pu entraîner une forme de dépersonnalisation par l’infantilisation, l’oppression, la déshumanisation, l’acculturation et l’aliénation des peuples colonisés. Pour l’Afrique, la nécessité d’une nouvelle rationalité s’impose : « la nouvelle rationalité qui permettra d’avancer dans la connaissance du réel, il faudra la bâtir pas à pas, en ayant une conscience aigüe de la difficulté et de la singularité du problème posé. » (Anta Diop : 180). Selon lui, le développement du continent africain repose en grande partie sur cette condition qui voudrait qu’après avoir identifié ses problèmes et défini les priorités, l’Afrique s’efforce à faire la science autrement, à la bâtir selon ses visions, pour mieux réussir son processus d’émergence.

Quoi qu’il en soit, cette émergence souhaitée par l’Afrique ne deviendra réalité que si elle s’appuie sur le type de motivation et les adversités à l’entrepreneuriat multisectoriel chez les jeunes scolaris·e·és et non scolarisé·e·s. Selon les priorités, voici quelques facteurs qui peuvent pousser les jeunes à entreprendre : la recherche d’une autonomie financière et par conséquent matérielle, le besoin d’augmenter ses revenus, le besoin de réalisation de soi, et enfin, la découverte d’une solution à sa pauvreté. Les freins à l’entrepreneuriat chez cette catégorie de personnes sont en général liés non seulement à un cadre législatif légal trop contraignant, à un environnement et à un climat des affaires souvent peu favorables, mais aussi à une insuffisance de créativité; celle-ci étant héritée de la pédagogie de répétition/restitution – et non pas de la pédagogie de questionnement/stratégie – au travers de laquelle elles ont été formées. Or, que ce soient les motivations ou les freins, ces facteurs tirent tous leur origine de la maîtrise ou non des éléments (outils et concepts) du projet à mener et du modèle sociétal existant (le contexte). Les jeunes Africain·e·s font ainsi face à une double difficulté : une difficulté d’ordre intellectuel en rapport avec les capacités mathématiques (Soriano, 1998; OCDE, 2007) et une difficulté d’ordre conjoncturel. L’organisation du secteur entrepreneurial reste très débattue en Afrique.

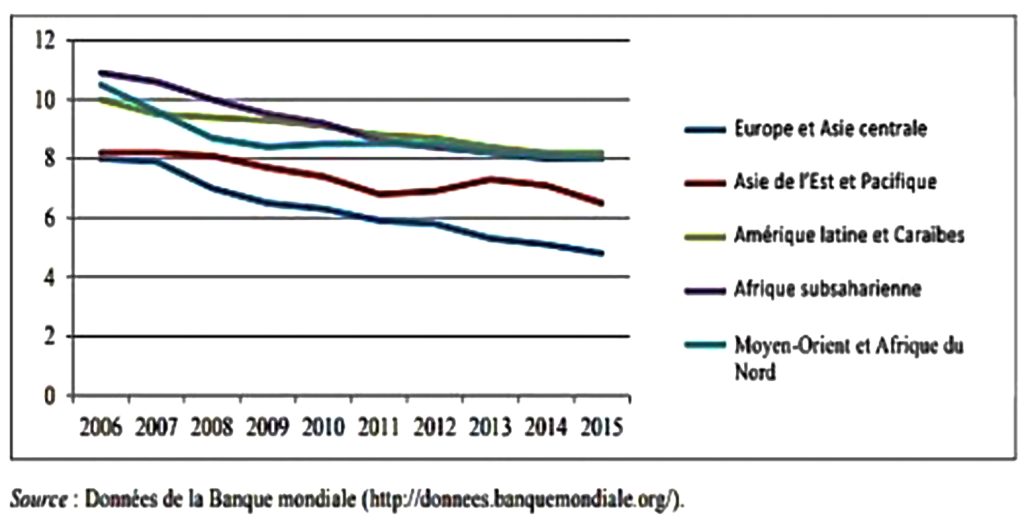
Le tableau ci-dessus montre qu’en Europe comme en Asie, les conditions de création d’une entreprise ont connu des allégements importants entre 2006 et 2015. Cependant, l’Afrique subsaharienne, malgré la grandeur de ses ambitions, reste un cadre peu propice en matière de création d’entreprise.

Aussi, la condition d’une émergence se trouve-t-elle dans un renversement de ces pesanteurs. Dans le cas spécifique des mathématiques, trop souvent, à la suite de quelques égoïsmes humains et des frustrations quant à leur bonne dévolution, elles engendrent des conflits de leadership (de nature non intellectuelle pour la plupart) et inspirent même parfois la méfiance dans les rangs des leaders et autres responsables de peu de foi. Ici, la contribution des responsables de l’éducation à cette transformation ne réside-t-elle pas dans un questionnement qui amènerait à s’interroger sur la nature, les principes et les motifs de l’enseignement des mathématiques?