De nombreux paramètres sont à prendre en compte lorsque l’on veut expliquer l’échec constaté chez les apprenant·e·s à la fois en classe de mathématiques et dans les filières mathématiques. Nous les regroupons en deux grandes catégories selon qu’ils prennent leurs sources à l’intérieur du système éducatif ou qu’ils proviennent des éléments extérieurs à ce système. Au début de l’année 2020, un élément inattendu, extérieur au système et sujet à de nombreuses controverses fait son apparition : la maladie à coronavirus (Covid-19). Cet élément a perturbé l’année scolaire par la fermeture complète de tous les établissements scolaires, universitaires et les autres structures d’éducation et de formation en présentiel. Nous nous devions alors de mesurer son impact sur les résultats scolaires. C’est ainsi qu’au regard des chiffres de 2020 relatifs aux performances des candidat·e·s en mathématiques à l’examen BEPC, indiquant un taux de réussite de 3,96 % sur un échantillon de 3 988 candidat·e·s (copies des candidat·e·s, salles de correction, nombre d’établissements…), nous constatons qu’au Kamerun comme dans la plupart des pays d’Afrique subsaharienne, après plus de quatre mois (de mi-mars à mi-juin) de confinement partiel, le niveau de performance en mathématiques des élèves candidat·e·s au BEPC est resté presque constant : 4,42 % en 2015, dans une situation normale sans incident important. Il s’agit là d’un indice à retenir^[1]. Les raisons fondamentales pouvant justifier l’échec dans cette matière pourraient se trouver bien au-delà de la qualité des activités de classe en présentiel, mais elles proviennent aussi et surtout de l’intérieur même du système éducatif.

Facteurs endogènes au système éducatif

Il s’agit des facteurs liés essentiellement à la gestion du système éducatif avec notamment la qualité des infrastructures, les ressources humaines, les programmes d’enseignement, la pédagogie de communication, de l’enseignement-apprentissage et l’expérimentation des mathématiques (Godot, 2005).

Le cadre structurel de l’enseignement et de l’apprentissage

Le décrochage scolaire, et partant l’échec en mathématiques est imputable à plusieurs facteurs. Parmi ceux-ci, on peut citer :

• les difficultés d’accès à un bon encadrement : les élèves des zones rurales sont très souvent enseigné·e·s par des non professionnels;

• l’organisation du travail par l’administration scolaire : les enseignant·e·s, qui sont déjà en nombre très insuffisant, sont pour la plupart submergé·e·s de travail et ne peuvent pas consacrer suffisamment de temps à chacun des apprenant·e·s comme on l’aurait souhaité;
• l’image négative attachée à cette discipline et répandue au sein d’un pan important de la société;
• la méconnaissance de l’impact direct ou indirect de cette discipline dans la gestion quotidienne des activités de tout homme en quête du mieux-être;

• une insuffisance d’initiatives d’émulation et de motivation à la fois chez les apprenant·e·s et les enseignant·e·s. Par exemple, l’emploi des critères peu rigoureux qui occultent le mérite comme outil de gouvernance scolaire et sociale est un choix très questionnable.

• les innombrables insuffisances qualitatives et quantitatives au niveau des équipements éducatifs, du matériel didactique, des infrastructures éducatives d’accueil (Greenwald & Thomley, 2012 : 28-31).

S’agissant de ce dernier facteur, le CONFEMEN l’évoque avec plus de détails et ajoute en même temps l’inadéquation entre les curricula et le matériel didactique dans certains pays.

L’état des lieux nous permet également de constater un déficit important de matériel didactique, dont les fournitures et les manuels scolaires. Non seulement les manuels sont rares au sein des écoles secondaires africaines, particulièrement dans les zones rurales, mais ils sont aussi mal partagés et mal gérés (volés, altérés, etc.), de sorte que le ratio livres/élève est bas. De plus, dans certains pays comme le Togo, une inadéquation entre les curricula et le matériel didactique est observée. (2008 : 41)

Par ailleurs, certain·e·s jeunes scolarisé·e·s manquent de livres de mathématiques au programme; d’autres n’ont pas du tout accès aux manuels de mathématiques pour diverses raisons : défaut de librairie dans leur localité et de bibliothèque dans leur établissement, prix relativement élevé du manuel sur le marché…

Comme le relève Perrin, l’on note également chez les enseignant·e·s du secondaire comme chez ceux et celles du supérieur, le peu d’intérêt accordé aux autres disciplines et une tendance à figer le mode de raisonnement lors des apprentissages.

Mais il y a aussi des points qui sont de notre ressort et qu’il est essentiel de prendre en compte. Je voudrais en citer deux.

D’abord, je crois que nous devons prêter plus d’attention que nous ne le faisons aux autres disciplines. Pour montrer que les mathématiques sont utiles, nous devons accorder plus de place dans nos enseignements aux activités de modélisation (et les discuter!). C’est ainsi que nous pouvons convaincre les autres, tous les autres, de l’importance des [sic] mathématiques.

Ensuite, s’agissant de l’apprentissage du raisonnement, il est important de ne pas le réduire à celui de la démonstration qui tourne souvent à l’exercice de style et dans lequel de nombreux élèves ont de la peine à rentrer. Il y a deux conditions pour cela. La première est de ne pas craindre d’étudier des problèmes ouverts (par exemple, en géométrie, les problèmes de lieux ou de constructions). La seconde est de disposer des bons outils pour faire des mathématiques. Par exemple, en géométrie encore, on peut penser que l’outil de transformations n’est pas le mieux adapté au niveau du collège et qu’il serait plus pertinent de lui préférer l’usage des invariants et des cas d’isométrie ou de similitude des triangles. (Perrin, 2004 : 20)

Certain·e·s jeunes, déçu·e·s par de mauvais résultats scolaires, découragé·e·s par des mathématiques trop exigeantes et contraignantes pour elles et eux, mis·e·s sous pression par certain·e·s enseignant·e·s qui ont maille à partir avec la pédagogie, abandonné·e·s à eux-mêmes et elles-mêmes par des parents trop occupé·e·s à autres choses, quittent l’école formelle pour entrer à l’école informelle ou s’installer dans la débrouillardise; une sorte de jungle humaine que les sociétés, mêmes modernes, n’ont toujours pas pu se défaire.

Aux raisons qui expliquent la désaffection des jeunes pour les mathématiques, Perrin en ajoute deux autres.

Il y a sans doute à cela des raisons sociales auxquelles nous sommes essentiellement étrangers : le statut de discipline dominante et de discipline sur laquelle se faisait la sélection a beaucoup nui aux mathématiques. De même, le développement de l’informatique, qui permet de faire sans peine des calculs autrefois réservés aux experts, a pu faire croire que les mathématiques étaient devenues inutiles.  (Perrin, 2004 : 20)

Sur le plan de la discipline en milieu scolaire, à force d’observer les comportements de plus en plus désorientés des jeunes et leurs moralités de moins en moins bonnes dans les formations scolaires, universitaires et même socioprofessionnelles, on a l’impression que la discipline qui fait partie de l’éthique et l’apprentissage des mathématiques ne sont pas compatibles. Un pan non négligeable de la jeunesse africaine actuelle est durement critiquable du fait de son penchant pour une délinquance marquée par la désobéissance, l’incivisme, la corruption^[2], etc. Ces comportements déshonorants, de déviance et de marginalité, entretenus par quelques-uns en son sein, sont-ils de nature à favoriser l’éclosion des sciences en général et des mathématiques en particulier dans leur milieu? Ces jeunes au rang desquels de jeunes inadaptés et de jeunes délinquants vrais devenus incontrôlables, quand ils sont interpellés par l’administration scolaire ou la police, s’organisent à résister face aux enseignant·e·s, parent·e·s et même la société entière qui, n’ont pas su, en temps opportun, leur indiquer les attitudes à adopter en tant que membres d’une communauté établie dans un environnement anomique^[3] en profonde mutation (Poitou, 1981; Demba et al., 2020). Une mutation manifeste dans un contexte d’inégalités et de violences, qui au demeurant, n’épargne pas la vie familiale et psychologique.

Une bonne part des comportements déviants résultent des conduites anomiques, témoignant de l’absence de normes consécutive à la déstructuration du groupe familial ou à l’éclatement de la cellule conjugale. (Poitou, 1981 : 114)

Cette déstructuration de la cellule familiale, plus observable en milieu urbain, vient renforcer le rôle déjà néfaste des conditions de la scolarisation dans le développement de la délinquance vraie dans ce milieu. La scolarisation à outrance (avec la multiplicité des institutions scolaires privées hors normes) semble très mal adaptée, étant donné la qualité de ses produits sur le marché de l’emploi, à la réalité africaine au sud du Sahara. Les « métis culturels » qu’elle génère paraissent à la fois déracinés et impuissants à s’intégrer dans le circuit économique moderne, faute de qualification adéquate et de débouchés suffisants (Poitou, 1981). Dans les zones urbaines, la présence quasi systématique des points de loisirs à proximité des institutions scolaires développe chez les apprenant·e·s un faible pour des fléaux tels que l’alcoolisme, la toxicomanie, la prostitution, le proxénétisme, les jeux de hasard, etc., gages des comportements déplacés et répréhensibles. Le passage de la délinquance primaire sans réelle gravité à une délinquance vraie est désormais plus facile.

Les causes véritables de la délinquance, toutes et étant complexes et contrastées en qualité comme en quantité, sont la résultante des conditions structurelles essentielles imposées par une situation d’anomie, consécutive à des changements sociétaux assez rapides et face auxquels les jeunes ont de la peine à s’adapter.

Les principaux facteurs de délinquance sont à rechercher d’abord dans la situation économique et dans les problèmes de la famille, dans les insuffisances du système scolaire et dans les frustrations créées par les conditions d’urbanisation des nouveaux citadins. (Poitou, 1981 : 122)

Le problème se pose aujourd’hui avec acuité, car les agents primaires de socialisation de l’enfant, à savoir le groupe familial et le système éducatif, ne sont plus capables de remplir entièrement leur fonction d’encadrement. C’est ainsi qu’une recrudescence des violences individuelles et collectives est enregistrée dans les milieux scolaires. Ce phénomène se manifeste par de multiples refus de respect et transgressions des règles sociales établies au sein des institutions scolaires et consignées dans un document spécial dénommé règlement intérieur. Feuzeu (2020) s’appuyant sur six (6) cas atypiques de violences recensés dans des établissements scolaires au Kamerun sur une période de quatorze (14) mois, observe une cristallisation des violences en milieu scolaire dans ce pays, avec des causes variées et la responsabilité des acteurs et actrices partagées.

À voir de près, les actes incriminés sont perpétrés par divers acteurs.  On dénombre les délinquants venus de l’extérieur de l’établissement, les élèves, les enseignants, les parents d’élèves, les hommes en tenue, l’administration scolaire et même l’autorité administrative. (Feuzeu, 2020 : 2136)

Des actes d’incivilité, agressions et accrochages sont fréquents entre les jeunes scolarisé·e·s ou non; et ce sont les enseignant·e·s et/ou les parent·e·s qui en payent parfois les frais^[4]. Ce genre de fait divers qui vient souvent perturber la quiétude des apprenant·e·s pourrait influencer directement ou indirectement les enseignements ou les performances en mathématiques de ceux ou celles-ci, surtout quand il survient entre deux ou plusieurs élèves, en salle de cours ou en dehors, pendant une leçon ou une évaluation de mathématiques. Le petit moment d’arrêt d’activités qui, en pareille circonstance, s’impose généralement aux acteurs didactiques en présence leur fait perdre un peu le fils de leurs idées.

En outre, s’agissant de la délinquance authentique, aujourd’hui dans les milieux carcéraux, la majorité des individus en détention provisoire ou préventive prolongée se recrute parmi les jeunes y compris les adolescents. Le cas des pays africains situés au sud du Sahara comme le Niger et le Nigeria (Poitou, 1981), le Gabon (Demba et al., 2020), le Kamerun (Feuzeu, 2020) et notamment celui de Madagascar est assez typique.

Dans les pays d’Afrique subsaharienne, la détention provisoire est utilisée de manière excessive et à titre de châtiment. En juin 2019, 28 045 personnes étaient détenues dans les prisons de Madagascar, qui dispose d’une capacité nationale totale de 10 360 places. Plus de 75 % des 977 adolescents détenus se trouvaient en détention préventive. (Muchena, 2020, paragr. 5)

Dans les milieux scolaires, un nombre non négligeable de jeunes garçons et filles, quand ils ou elles ne s’autocensurent pas en abandonnant l’école ou les cours de mathématiques volontairement, ils ou elles sont souvent, pour diverses raisons, exclu·e·s temporairement ou définitivement des établissements avant même la fin de l’année scolaire^[5]. Et quand parmi ces présumé·e·s délinquant·e·s figurent un·e élève qui travaille mieux en mathématiques en classe, le groupe de travail dont il ou elle faisait partie connaîtra inéluctablement un vide dû à son absence. Toutefois, d’autres élèves se montrent plus entreprenant·e·s dans les activités post et périscolaires. Ici encore, les taux d’adhésion dans les clubs à caractères scientifique et technologique restent très faibles, presque dans les mêmes proportions que les taux d’inscriptions dans les filières correspondantes. Les jeunes ne semblent-ils/elles pas plus intéressé·e·s par le sport, la danse, les voyages et les clubs de photographie ou des amis invisibles? Il s’agit des milieux dans lesquels ils ou elles mènent des activités qui, pensent-ils ou elles, n’ont rien à voir avec les mathématiques et ses exigences.

Sans toutefois effectuer un travail de sociologue, il nous semble opportun de souligner un fait social qui pourrait sans doute exercer une influence quelconque avec le sujet qui nous préoccupe. Ce fait se traduit par ce que nous appelons jeunesse de façade politicienne. Il s’agit de cette catégorie de jeunes qui nait et se développe aux côtés des archétypes socioéducatifs. Des jeunes Africain·e·s qui, sans être militant·e·s, se regroupent dans des mouvements ou autres associations à caractère socioculturel et/ou politique, à l’effet de soutenir un leader social, modèle de leurs rêves. Ces jeunes qui désertent pour des raisons diverses les milieux scolaires et universitaires pour rentrer, soit dans ces sortes de « fans clubs », soit dans la rue, ne se livrent-ils/elles pas à toutes formes de déviances qui sont susceptibles de compromettre leurs performances scolaires ou universitaires, et par suite leur avenir? D’autres s’investissent soit dans les salles de jeux de hasard, gaspillant de l’argent reçu ou dérobé subtilement à leurs proches ou parent·e·s, soit ils ou elles se livrent à la petite délinquance, décourageant et déroutant ainsi certain·e·s parmi leurs pairs qui n’aspirent qu’à aller normalement à l’école. Les conséquences de ce fait sont rattachables aux causes des échecs de la jeunesse, dans divers secteurs y compris l’école moderne et « ses » mathématiques.

Aujourd’hui, les jeunes trouvent leurs modèles et leurs idoles en dehors des secteurs d’activités qui nécessitent un certain type d’intellect. C’est ainsi qu’un nombre important de jeunes s’intéresse davantage aux sports, à la musique ou au cinéma, multipliant des challenges dans ces domaines; ceux-ci, à quelques exceptions près, brassent beaucoup d’argent et font régner le principe du pot-de-vin. Beaucoup sont sollicités à temps partiel par de grandes firmes commerciales pour participer à des ventes promotionnelles de certains produits, à des caravanes et autres spectacles interminables de musiques au cours desquels les jeunes filles et garçons sont souvent soumis à toutes formes de harcèlements. Notre propos n’est pas de dire que les métiers de divertissement sont dépourvus de valeurs, mais plutôt de questionner les choix, les profils et les motivations qui conduisent les jeunes à embrasser de telles activités (Sako, 2010). Si l’on interroge ceux-ci et celles-ci sur leur projet de vie, ils sont très peu à vouloir porter leur premier choix sur ces métiers. Beaucoup y vont par mimétisme et se retrouvent souvent piégé·e·s. Il faut toutefois noter que la précarité dans laquelle certain·e·s jeunes se retrouvent ne leur laisse pas beaucoup d’options. Ils doivent pouvoir affronter de telles difficultés et aller de l’avant.

Dans nos écoles, l’on constate facilement qu’un certain nombre de jeunes font les mathématiques sans engouement, simplement parce que tel qu’elles sont enseignées, elles n’exercent pas d’attrait sur ces enfants; elles leur semblent imposées par le système. Pour ceux et celles qui s’en sortent mieux en mathématiques, des automatismes de calcul s’installent au cours de la pratique régulière des exercices, leur permettant de construire des schémas de problèmes. Tout se passe comme si l’apprenant·e et l’enseignant·e avaient construit chacun et chacune une mémoire des problèmes déjà rencontrés, ainsi que des savoir-faire de résolution associés. Cette forme de mémoire s’organise grâce à un certain catalogage et un recours à des problèmes prototypiques représentatifs de chaque catégorie de problèmes déjà rencontrés. L’apprenant·e peut alors être capable de mobiliser à bon escient le modèle le plus adapté pour résoudre le problème posé lors d’une évaluation de connaissances ou de compétences. Bien que ce soit positif, l’élève développe le plus souvent des itinéraires techniques, c’est-à-dire des procédures toutes faites sans originalité particulière, héritées d’un système éducatif visant essentiellement à rappeler, restituer les connaissances acquises plutôt qu’à penser parfois autrement face à des problèmes fussent-ils isomorphes (Van Nieuwenhoven, 2014).

Ainsi, nous avons pu observer que des éléments tels que la qualité des infrastructures, des enseignant·e·s, les méthodes d’enseignement/apprentissage et d’encadrement des apprenant·e·s, ainsi que les types d’évaluation sont susceptibles d’affecter négativement la réussite scolaire, particulièrement en mathématiques. Sur les trois derniers éléments sus-cités, la CONFEMEN fait observer qu’

en Afrique subsaharienne, le nombre d’enseignants qualifiés est insuffisant pour répondre à la demande croissante des établissements d’enseignement secondaire provoquant ainsi l’embauche massive d’enseignants sans formation adéquate. (2008 : 41)

Cependant, il existe des éléments relevant notamment du dispositif d’enseignement/apprentissage qui contribuent à une situation d’échec : les leçons de mathématiques de certain·e·s enseignant·e·s titulaires, qualifié·e·s et non qualifié·e·s, permanent·e·s ou vacataires semblent encore et toujours en rupture avec les autres activités de la classe, non contextualisées et dépourvues de liens interdisciplinaires. Ce qui conduit, assez souvent, à une ambiance de classe particulière, faite d’exigences, de méthode, d’ordre, de rigueur, de vocabulaire, de langue et de métalangue. Dès lors, les mathématiques représentent, aux yeux des apprenant·e·s, un domaine réservé, engendrant par la même occasion des comportements de rejet; attitude dont il devient difficile de se défaire à la longue.

Des indicateurs de performances médiocres

Les jeunes en âge scolaire au Kamerun comme dans plusieurs pays d’Afrique (CONFEMEN, 2008) renoncent, dans leur majorité, aux disciplines et secteurs socioprofessionnels dont la formation initiale exige une réflexion mathématique, aussi petite soit-elle, pour embrasser des filières qui, pensent-ils, n’ont rien à voir avec cette matière. D’après Berger (2005), Le Cam & Selles (2016), cette fuite de la jeunesse en âge scolaire, couplée aux échecs enregistrés dans cette discipline est assez notoire dans la plupart des pays africains subsahariens, et même dans certains pays en voie d’émergence. Ces indicateurs reviennent dans divers aspects sociaux en relation avec l’éducation en général. L’UNESCO, dans son Rapport mondial de suivi sur l’EPT^[6] de 2005, donne quelques chiffres assez parlants (Pilon, 2006). Pour ce qui concerne les taux de renonciation et d’échec en mathématiques, par exemple, la situation reste préoccupante. Sur le terrain, et en situation de classe notamment, il y a une sorte d’inertie qui caractérise très souvent les séances de leçons ou de travaux dirigés de mathématiques. Il y a également la persistance des difficultés liées à la bonne connaissance des outils fondamentaux en mathématiques par les apprenant·e·s et certain·e·s enseignant·e·s^[7]. Dans l’optique d’agir positivement sur ces indicateurs, plusieurs travaux sont conduits quotidiennement dans divers laboratoires de recherche en science de l’éducation depuis des décennies. Le thème fédérateur de ces travaux de réflexion concerne essentiellement l’amélioration des programmes, des enseignements, des apprentissages et la pratique des mathématiques en Afrique.

Pour Touré par exemple, les pays francophones doivent :

non seulement préparer leurs citoyens à comprendre et appliquer les mathématiques dans la vie de tous les jours, mais aussi, assurer la formation des mathématiciens utiles à leur développement économique, scientifique et technologique. (2002 : 6)

La solution proposée par Traoré et Barry est de partir d’une distinction fondamentale :

il existe des problèmes isomorphes (au sens des mathématiciens) dont les solutions diffèrent considérablement selon qu’ils sont posés en contexte scolaire ou en contexte de la vie quotidienne. (2007 : 3)

Enfin, Sokhna & Sarr ont proposé dans le cadre de l’Université virtuelle africaine de capaciter les enseignant·e·s de mathématiques en concevant des dispositifs de formation continue et à distance, ainsi que des ressources susceptibles de les aider dans leur profession. Ils inscrivent leur projet dans une dynamique qui ferait passer d’une « formation d’enseignants aux mathématiques » à une « formation d’enseignants de mathématiques » (2009 : 1). En d’autres termes, il est question d’amener les enseignant·e·s de mathématiques à réfléchir sur leurs pratiques d’enseignement-apprentissage-expérimentation et à concevoir des outils pédagogiques efficaces de sorte qu’on assiste plus à une simple juxtaposition d’automatismes coupés de la réalité. De manière globale, les résultats de ces travaux sont des œuvres partagées par une catégorie d’enseignant·e·s de mathématiques pétri·e·s d’expériences africain·e·s ou non, des inspecteurs et inspectrices de pédagogie, des chercheurs et chercheuses en science de l’éducation (Godot, 2005 : 137-212) et autres formateurs et formatrices chevronné·e·s faisant dans la formation initiale et continue des enseignant·e·s du primaire et du secondaire, et par quelques chercheur·se·s en didactique.

Dans les programmes actuels d’enseignement des mathématiques du secondaire de la plupart des pays africains, il ne figure pas de contenus explicites, aussi réduits soient-ils, sur l’histoire de cette discipline ni sur celle de ses diverses théories. Au Kamerun et à l’université de Ngaoundéré par exemple, un cours d’épistémologie des sciences a été supprimé des programmes d’enseignement du département des mathématiques et d’informatique de la faculté des sciences dans les années 2010. Dans les écoles normales supérieures, quelques thèmes sur le caractère transversal et l’interdisciplinarité des mathématiques avec d’autres sciences sont timidement abordés par des élèves-professeur·e·s de mathématiques dans leurs mémoires de fin de formation (Kono, 2014). Pourtant, les mathématiques, comme les autres sciences, sont une construction, une culture qui se perfectionne au fil de l’histoire et du temps. L’enseignement de l’histoire des mathématiques apporte une dimension culturelle indéniable aux processus de transmission et d’acquisition des savoirs de ce champ disciplinaire. Il permet à l’apprenant·e d’affronter les incertitudes « mathématisables » ou non avec beaucoup plus de conviction.

Certains étudiants peuvent avoir le sentiment que cet enseignement est inutile, car il ne donne pas un accès immédiat aux théories mathématiques modernes et efficaces. Cela est vrai, mais après tout, les mathématiques paraissent elles aussi souvent inutiles. Le but d’un enseignement d’histoire des sciences et de culture scientifique est le même que celui d’un enseignement de sciences traditionnel : il permet de transmettre l’expérience de nos prédécesseurs. L’histoire permet de prendre du recul par rapport aux évènements immédiats; la culture permet d’avoir des repères. (Baumann, 2004-2005 : 10)

L’utilisation d’éléments d’histoire des mathématiques dans l’enseignement en classe comme dans la formation initiale et continue des enseignant·e·s ne peut se faire qu’à travers une didactique des mathématiques adéquate (Clinard, 1993). Il n’est pas toujours aisé de se les approprier, de les maîtriser ou de les assimiler sans se remettre en question (Villani, 2010). Et la remise en question parait impérative pour tout type de discours qui se veut scientifique. À ce propos, Bachelard ne disait-il pas qu’« on connait contre une connaissance antérieure, en détruisant des connaissances mal faites. » (1398 : 14)?

Par ailleurs, l’inadéquation entre les profils des élèves et les épreuves auxquelles ils et elles sont soumis·e·s lors de certains examens et/ou concours pose un véritable problème d’ordre pédagogique. Au Kamerun par exemple, les effectifs réduits au second cycle des lycées d’enseignement technique pourraient résulter du fait que le faible nombre d’élèves titulaires d’un Certificat d’aptitude professionnelle (CAP) venant des premiers cycles du même ordre d’enseignement est obligé de passer un concours pour accéder au second cycle, au même titre que ceux et celles qui viennent de l’enseignement général. Paradoxalement, l’on constate, pour le déplorer, que parmi les épreuves écrites de ce concours ne figure aucune épreuve de matières professionnelles. Elles se limitent exclusivement aux trois matières que sont le français, l’anglais et les mathématiques. C’est ainsi qu’un nombre important de jeunes titulaires d’un CAP qui pour la plupart ne sont pas souvent brillants dans les matières d’enseignement général, et qui sont refusé·e·s, se retrouvent abandonné·e·s à leur sort et obligé·e·s de se lancer sans expérience dans la vie active ou dans la débrouillardise. Est-ce cette catégorie de technicien·e·s qui permettra à l’Afrique d’atteindre l’émergence? Une pédagogie différenciée aurait pu distinguer les profils et trouver des dispositifs d’évaluation (étude des cas ou des projets) qui soit en corrélation avec les spécialités, les prérequis et les pré-acquis de chacune des catégories de candidat·e·s à ce concours.

En outre, quel intérêt tire-t-on à présenter des statistiques équivoques aux examens certificatifs, avec à terme, à défaut du statu quo, plutôt qu’une dégénérescence généralisée et progressive de la vie scolaire et postscolaire dans presque tous les secteurs d’activités de la communauté?

Facteurs exogènes au système

Des pesanteurs systémiques sur le continent africain

Sans être exhaustif, les possibles pesanteurs non moins négligeables que connaissent les développements socioéducatif, économique et intellectuel de l’Afrique sont de plusieurs ordres :

Les marques profondes de la traite et de l’esclavage négriers transatlantiques ont arraché à l’Afrique noire ses valeurs et ressources humaines les plus valeureuses sur les plans à la fois intellectuel, physique et psychologique; laissant ainsi présents dans les esprits et les cœurs des Africain·e·s de multiples victimisations et des conséquences indélébiles et intergénérationnelles. Les séquelles actuelles telles que « la faible confiance en soi, la faible estime de soi, la hiérarchie de la couleur, le racisme interne. » (Tagodoé, 2011 : iii) dont souffrent les Afro–descendant·e·s seraient à l’origine d’un trauma congénital : « le syndrome ou trouble post-traumatique découlant de l’esclavage. » (Tagodoé, 2011 : 1-2). Le pressentiment de Tagodoé nous semble un peu excessif, questionnable et mérite d’être pris avec beaucoup de réserves. En effet, pour lui, des jeunes d’Afrique d’aujourd’hui connaitraient des difficultés en mathématiques parce qu’ils et elles sont l’objet d’un trouble post-traumatique issu de l’esclavage. Nous pensons que non! On ne peut pas expliquer rigoureusement les problèmes de la société africaine contemporaine par le recours à des faits historiques aussi lointains. Les Africain·e·s doivent avec plus de sérieux agir sans complaisance pour la construction de leur destin en dépassant ce genre de frustrations combien dévalorisantes pour la personne humaine.

L’Afrique est un continent anciennement ouvert au monde, mais toujours resté à la traîne dans presque tous les domaines porteurs de développement. De même, de longues années de famine, de maladie et de guerres renouvelées avec pour corollaires l’insécurité alimentaire, sanitaire et éducative : il y a encore des poches visibles et permanentes de la famine, des maladies (paludisme, sida, Ebola, etc.) et de la sous-scolarisation çà et là sur le continent. En plus, l’instabilité géopolitique : l’absence d’une paix permanente couplée à l’instabilité politique dans de nombreux pays. On observe des coups d’État récurrents, une insécurité permanente, des institutions politiques peu stables, la fuite des cerveaux et l’exode des jeunes vers d’autres horizons. La fuite des cerveaux qui engendre l’exode des ressources humaines aux qualités intellectuelles avérées s’est accentuée au fil du temps. Cependant, des pistes de solutions à cette dynamique sociale d’envergure existent (Gaillard A. & Gaillard J., 2006).

Dans une approche naïve, le lectorat peut se demander quelles relations l’apprentissage des mathématiques peut entretenir avec la traite négrière, la famine ou l’instabilité politique. Notre démarche vise à prendre l’enseignement/apprentissage des mathématiques comme un élément constitutif d’une société qui doit garantir dans son ensemble des conditions d’éclosion, de développement et de rayonnement des formes de savoirs et de savoir–faire. En effet, comment envisager une réussite à la fois intellectuelle et sociale dans un contexte où règnent des frustrations, des préjugés, des maladies, de l’instabilité en toute chose, etc.?  Notre propos est de dire que le visage que présente le continent africain actuellement n’est pas propice à son propre développement global. Des auteurs comme Vergnaud (1982) et Vellard (1988) n’ont-ils pas montré l’importance des facteurs psychologiques et cognitifs dans le processus d’apprentissage?

On observe un continent profondément inégalitaire et dépendant. L’accès à une bonne structure d’éducation en Afrique par la majorité des jeunes Africain·e·s est très difficile, voire différencié; les inégalités sociales sont facilement perceptibles.

L’Afrique reste l’une des régions du monde dans laquelle les inégalités sont les plus marquées, étant donné qu’elle abrite 10 des 19 pays les plus inégalitaires de la planète. Les niveaux d’inégalité élevés à travers le continent posent un sérieux défi à la réalisation de l’objectif primordial de « ne laisser personne de côté » à l’horizon 2030. (Odusola, Cornia, Bhorat & Conceição, 2017 : 23)

Par ailleurs, la très insuffisante audibilité de la pensée africaine^[8] constitue un véritable frein. Consécutive au néocolonialisme, cette audience lacunaire, pour de nombreux auteurs et autrices, est entretenue par des dispositifs inéquitables de production et de diffusion des savoirs. C’est ainsi que Piron parle d’une invisibilisation de certaines catégories de savoirs : « Au cours de mes recherches, j’ai découvert à quel point les savoirs des acteurs étaient pris dans les formes de pouvoir qui pouvaient invisibiliser d’autres formes de savoirs notamment ceux des femmes et ceux des pays du Sud. » (2019, en ligne). Cette action préjudiciable à la diversité des formes de savoirs aboutit le plus souvent, comme le montre d’ailleurs Piron, à une négation de la pensée des autres : « On nie la singularité des auteurs qui souffrent de ne pas pouvoir agir dans la société à travers leurs recherches et qui ne finissent par [sic] ne plus voir leurs responsabilités sociales. Or, un chercheur est toujours situé dans une langue, un pays, un genre, une histoire. » (2019, en ligne). Ce sont des écueils majeurs à l’expression de la pensée africaine.

Dans la même logique, à l’observation des politiques de relations internationales et de développement agricole adoptées par plusieurs pays de l’Afrique francophone au lendemain des années 60, Dumont en visionnaire mettait déjà en garde cette partie du continent africain, à travers un premier cri d’alarme dans son célèbre ouvrage, L’Afrique noire est mal partie (1962). En effet, dans une analyse assez critique des sociétés africaines qui tranche avec les considérations géopolitiques de l’époque, il avait présenté les problèmes de déséquilibre dans la qualité de l’éducation et les types de formations à donner à la jeunesse, montré les préjudices désespérants de ces problèmes pour l’Afrique noire et proposé des pistes salvatrices. Plus d’un demi-siècle après, au vu des niveaux d’éducation et de développement des pays de cette partie du monde, l’on peut affirmer qu’il avait vraiment des raisons sérieuses de s’inquiéter pour notre avenir. Le même auteur avait, avec Mottin, quelques années plus tard, tiré la sonnette d’alarme pour la seconde fois dans L’Afrique étranglée (1980). Les auteurs se demandent si l’Afrique pouvait encore échapper aux désastres socioéducatifs et socioéconomiques qui leur semblaient alors inéluctables. Senghor, alors président de la République du Sénégal, déclara à Dumont : « Je dois reconnaitre que, au début, je vous ai beaucoup critiqué. Aujourd’hui, je suis obligé d’admettre que j’ai eu tort : c’est vous qui aviez raison. Nous aurions dû suivre vos conseils. » (Dumont & Mottin, 1980 : 15). Cet aveu d’un décideur politique africain de choix, qui arrive plusieurs décennies après, aurait certainement eu toute son opportunité s’il était dit à date; il est évident que le Sénégal, et à travers ce pays, l’Afrique noire toute entière auraient connu pendant tout le temps galvaudé, une avancée significative en matière d’éducation et de développement multisectoriel par rapport à leur niveau actuel.

Comme on peut le constater, les écueils sont nombreux. Nous ne nous attarderons pas davantage sur cette question d’autant plus que de nombreux travaux de recherche ont été menés et d’autres encore sont en cours, dans lesquels des pistes de solution sont esquissées (Pourtier, 2010; Hot et al., 2014). Pour nous, la reconnaissance de l’existence de ces problèmes constitue déjà un premier pas vers leur résolution dans la durée. Cette résolution ne pourrait se départir à la fois d’un ancrage et d’un ressourcement aux valeurs fondamentales, éthiques et matérielles de l’Afrique.

Absence de considération des avantages intrinsèques de l’Afrique

Par avantages intrinsèques, nous entendons les ressources naturelles, les valeurs en termes d’atouts humains, socioculturels et environnementaux dont dispose le continent africain pour impulser et soutenir son développement. Ceux-ci sont nombreux et propices au redéploiement des sciences mathématiques.

On observe que :

• L’Afrique est dotée d’une bonne réserve de ressources humaines sur le continent comme dans sa diaspora. On note sur ce continent une forte croissance démographique^[9].

• Elle possède de grandes réserves naturelles du sol et du sous-sol non encore exploitées; de faibles fréquences de calamités naturelles : tremblements de terre, aléas climatiques (inondations, sécheresse…).

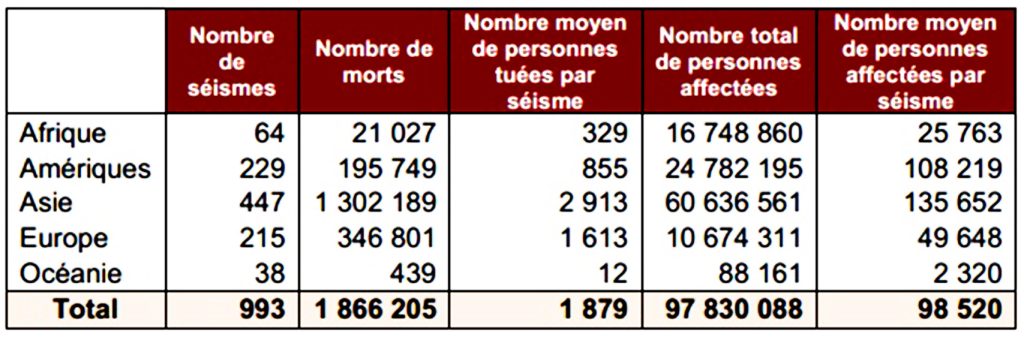
L’avant-dernière colonne à droite indique le nombre de personnes en état de besoin critique d’aide en nourriture, eau, abri, hygiène ou assistance médicale d’urgence. Ce tableau indique que l’Afrique occupe la deuxième position du classement des continents les moins secoués par les mouvements tectoniques. Enfin, des savoirs endogènes des peuples qui peuvent encore être codifiés et insérés dans les systèmes éducatifs^[10] afin que les finalités éducatives fixées cadrent avec l’idéologie de la pensée africaine.

L’Afrique dispose entre autres d’une population assez jeune : dans un contexte de bonne gouvernance, cette jeunesse, si elle est bien encadrée par une éducation de bonne facture, disons mathématique, elle sera très imaginative, ingénieuse et ouverte aux questions de développement. Bref, une jeunesse résiliente capable de vivre et de travailler dans des conditions parfois difficiles (conditions de scolarisation, conditions de formations initiale ou continuée, résistance quotidienne à diverses formes de pression et autres stress).

Sur ce point, Pourtier trouve que :

Le continent le plus pauvre est en effet le continent le plus jeune : les moins de quinze ans y représentent près de 45 % de la population, ce pourcentage frôlant les 50 % au Niger et en Ouganda. Par comparaison, cette catégorie d’âge ne compte que pour 15 % de la population de l’Europe. (Pourtier, 2010 : 102)

Contrairement à Pourtier, pour qui la structure démographique des pays subsahariens constitue un handicap pour leur accès rapide à l’éducation, nous pensons que la jeunesse de leurs populations est un avantage. Il est vrai que l’investissement pour leur formation représente un coût important qui, heureusement, peut être supporté par les revenus des produits du sol et du sous-sol de ces pays.

 Bref, l’Afrique est un continent en devenir qui aspire à l’émergence. Elle peut encore prétendre parler d’universalité scientifique, car des problématiques nouvelles y sont encore possibles et nombreuses en matière de recherche. Elle demeure un véritable chantier de réflexion et d’innovations technologiques, propice à la mise en œuvre de nouvelles pédagogies, à l’exemple d’une forme de pédagogie hybride que nous avons conçue et que nous nommons approche pédagogique par les capacités/compétences, la stratégie et l’inventivité (APCSI)^[11].