13 Análisis espacial

Análisis espacial

Definición del método Método de análisis para medir el grado de similitud de un lugar con sus vecinos

Fortalezas del método Los resultados de la cartografía pueden explicarse fácilmente a los decisores y al público en general

Desafíos del método No tiene en cuenta otros factores que pueden influir en los resultados de la intervención (por ejemplo, las características ambientales, el cambio de las precipitaciones y/o las condiciones atmosféricas, etc.). Es necesario integrar en el protocolo de evaluación la adquisición de datos geolocalizados de una muestra geográfica. Se requieren conocimientos básicos de análisis espacial.

El objetivo de los métodos de análisis espacial es determinar las características de la distribución espacial de las unidades geográficas (por ejemplo, los hogares) o sus valores (por ejemplo, el número de casos de dengue en el hogar). Estas características pueden analizarse globalmente, es decir, a gran escala, como una ciudad entera, para lo cual los métodos mostrarán la nube de puntos de las unidades geográficas, las relaciones espaciales entre los valores y los individuos (dependencia espacial), y las características geométricas (la organización de los valores en el territorio, como un gradiente norte-sur, por ejemplo) de la nube de puntos o los valores. Cuando los valores estudiados son cuantitativos, es posible analizar la distribución geográfica de los valores asociados a los individuos, examinando en particular si existe una relación con la proximidad entre estos individuos. El análisis adopta la forma de un índice que expresa si existe o no una correlación entre el valor de los individuos y su proximidad. Por ejemplo, permite caracterizar si los valores similares tienden a ser cercanos en el territorio o, por el contrario, están totalmente dispersos. Si se agrupan los valores, hablamos de una autocorrelación espacial positiva. Si se dispersan, hablamos de autocorrelación espacial aleatoria. Por lo tanto, este método tiene como objetivo caracterizar la dependencia espacial de los valores.

Muchas situaciones en la atención sanitaria no son homogéneas (también llamadas estacionales). Nos referimos particularmente en la concentración de casos de enfermedad en localidades muy específicas, unas pocas calles de un barrio, por ejemplo. Imaginemos un barrio cuyo borde está cerca de una presa. Los casos de paludismo existen en todas partes en esta zona, pero están más presentes y concentrados en la calle que bordea la presa. La distribución espacial ndel paludismo sería en este caso heterogénea a nivel del barrio. Sin embargo, las medidas globales de autocorrelación espacial, a escala de todo el vecindario, pueden enmascarar este fenómeno de concentración localizada cuando la autocorrelación varía de un lugar a otro. El índice de autocorrelación espacial obtenido podría significar que la distribución espacial de los casos de paludismo es homogénea en el vecindario, ya que el cálculo, aplicado a todo el territorio, podría minimizar la concentración identificada en la calle cercana a la presa. En esta situación se dice que hay asociaciones espaciales de valores locales significativos que no son detectables por la medida clásica de autocorrelación espacial global definida por Moran, por ejemplo.

Uno de los objetivos del análisis espacial es detectar formas o lugares singulares en los que se producen altas concentraciones locales de valores, también llamados agregados (de individuos o valores). Así pues, se dispone de métodos para realizar análisis locales muy precisos, lo que resulta útil para orientar determinadas acciones, por ejemplo. Luc Anselin (Anselin, 1995) ha desarrollado un índice para compensar el efecto de la ocultación de las autocorrelaciones locales por los índices globales: el Indicador local de asociación espacial (LISA) (Local indicator of spatial association).

El LISA mide si hay lugares cuyos valores locales están significativamente relacionados con la proximidad de esos lugares y si hay agrupaciones de valores muy altos o muy bajos entre esos lugares. Por lo tanto, estos indicadores miden la concentración de los valores numéricos medidos en un conjunto de puntos. El cálculo se basa en la autocorrelación global de Moran, como la media de los productos de los valores normalizados de los pares de puntos, ponderados por un peso espacial que se representa por la distancia. El análisis LISA se realiza en cada hogar, representado por un punto, y en las relaciones de cada hogar con sus vecinos. Consiste primero en calcular un índice para cada punto (hogar) de su vecindario. Los indicadores estadísticos expresan el grado de confianza y la importancia que se puede dar a la información adquirida. En el caso de unidades espaciales irregulares para las que sólo se tiene en cuenta la matriz de cercanía, el peso es igual a 1 cuando las unidades son contiguas y 0 para las demás. Así, alrededor del punto observado, el LISA local determina la extensión de una región (cluster) formada por puntos que tienen valores cercanos a los suyos. La suma de las LISAs locales es proporcional al indicador global. El indicador local se calcula de manera similar al índice de Moran. La interpretación de las LISA obtenidas se basa en supuestos estadísticos de normalidad. Por consiguiente, es necesario comprobar la importancia estadística de las estructuras de los clusters en la región. Se calcula un valor p para cada punto: cuanto más bajo es el valor p, más significativa es estadísticamente la existencia de cualquier cluster que forme con sus vecinos (Caloz y Collet 2011). Esto resulta en cinco casos. El primero es cuando el valor p no permite rechazar la hipótesis nula: el punto no se considera significativo para ser agregado a otro punto. En los otros cuatro casos, los índices LISA se utilizan para una tipología de cuatro cluster, según el valor del individuo y el valor del barrio. Estos cluster están representados en la tabla 1, con el color que se utiliza habitualmente para su cartografía (Oliveau 2010).

Por consiguiente, este tipo de método es adecuado, pero se utiliza raramente, para evaluar los efectos de una intervención en el espacio, a escalas geográficas muy finas, como la ubicación de los hogares, por ejemplo. Los valores analizados a nivel de hogar (coordenadas geográficas) pueden representar, por ejemplo, a varias personas afectadas por una enfermedad (datos cuantitativos). El LISA se calculará y mapeará antes y después de la intervención para evaluar los efectos.

Análisis espacial de los efectos de una intervención comunitaria de control del dengue en Uagadugú

Tras varias fases de aparición del dengue en Uagadugú (Burkina Faso), se decidió elaborar y aplicar una intervención de base comunitaria para controlar el mosquito Aedes aegypti, principal vector del dengue en las zonas urbanas.

El ámbito del estudio y los participantes

El estudio se llevó a cabo en dos barrios comparables de Uagadugú (Tampouy y Juvenat), seleccionados entre cinco zonas identificadas de la ciudad. En efecto, en los dos barrios hay perfiles socioeconómicos muy contrastados: hogares acomodados que viven en casas modernas de hormigón que se abastecen totalmente de las redes de agua y electricidad, pero también hogares con un nivel de vida muy bajo en casas construidas con arcilla, a veces sin servicios básicos (Observatoire des populations de Ouagadougou 2013). Estos barrios se caracterizan también por zonas en las que no se lleva a cabo regularmente la gestión de residuos y en las que se acumulan desechos en determinadas calles, lo que favorece la proliferación de mosquitos.

Tampouy, que se encuentra en la parte noroccidental de la ciudad, fue seleccionada al azar para recibir la intervención, mientras que Juvenat, en la parte oriental de la ciudad, fue elegida como distrito de “control”, para comparar situaciones. En cada barrio delimitamos una zona con un radio de un kilómetro alrededor del centro de salud primaria (considerado como un punto de referencia). En Tampouy, la intervención se llevó a cabo dentro de este perímetro. Se utilizaron las coordenadas geográficas de los hogares para dibujar 287 hogares en Tampouy y 289 hogares en Juvenat dentro de este perímetro (dibujar sin reemplazo) a fin de reunir los datos entomológicos (larvas y pupas de mosquitos) necesarios para evaluar el impacto de la intervención.

La teoría de la intervención

1. Movilización y organización: este paso permitió establecer contacto con los líderes comunitarios y las asociaciones formales e informales que trabajan en la zona de intervención de Tampouy para informarles de la situación del dengue en su barrio. Este paso promovió la concienciación de personas influyentes sobre la situación de esta enfermedad y su participación en la lucha contra ella.
2. Planificación operativa: consistió en un desarrollo participativo de la intervención con la intervención de personas influyentes y asociaciones dispuestas a participar.
3. Acción comunitaria: consistía en la realización de las actividades de intervención por parte de los miembros de la comunidad (facilitadores comunitarios y grupo de teatro) en beneficio de la comunidad. Esas actividades tenían por objeto alentar la participación efectiva de los hogares y la población.
4. Monitoreo/evaluación dirigida por la comunidad: esto permitió una mejor participación de la comunidad.

La interacción de estos diferentes componentes tuvo como efectos directos, el aumentar el conocimiento sobre el dengue y las enfermedades febriles transmitidas por vectores, fortalecer la capacidad de la comunidad en la zona de intervención y reducir los índices entomológicos. El presente capítulo no tiene por objeto describir estos resultados.

Los efectos distales previstos son el mantenimiento de la lucha contra los mosquitos, lo que dará lugar a una reducción de la población de vectores del dengue y el paludismo y, por consiguiente, a una disminución de los episodios y hospitalizaciones relacionados con el dengue y el paludismo.

Valoración

En la tabla 2, resumimos la estimación de la evaluación de esta intervención en el contexto específico de este capítulo.

Tabla 2 : Resumen del diseño de evaluación de la intervención comunitaria para combatir el dengue

Objetivo de la evaluación	Preguntas de evaluación	Planificación
Evaluar el impacto de la intervención en la densidad y distribución geográfica de las larvas y pupas de Aedes aegypti en el distrito de Tampouy.	¿Disminuyó el número de larvas y pupas en Tampouy después de la intervención en comparación con “Juvenat”, que no recibió intervención? Tras la intervención, ¿persisten en Tampouy zonas de densidad de larvas y pupas en comparación con el “Juvenat” que no recibió intervención?	Estudios entomológicos previos a la intervención, octubre de 2015: los encuestadores buscaron y recogieron larvas y pupas de Aedes aegypti en cada concesión visitada en los dos distritos. De junio a principios de octubre de 2016: realización de actividades de intervención en Tampouy. Estudios entomológicos después de la intervención de finales de octubre a principios de noviembre de 2016: las personas investigadoras buscaron y recogieron larvas y pupas de Aedes aegypti en cada concesión visitada en los dos distritos.

Aplicación del método LISA

Los Indicadores de Asociación Espacial Local permiten la exploración espacial local del impacto de la intervención comunitaria para combatir el Aedes aegypti en el distrito de Tampouy de Uagadugú. Sobre la base de los datos de los estudios entomológicos realizados antes y después de la intervención, el procedimiento de análisis consta de tres pasos: 1) cartografía de la distribución espacial del número de larvas y pupas, 2) medición de esta distribución, y 3) cálculo de los indicadores de asociación espacial local y cartografía de los mismos.

Etapa 1: Análisis de la distribución espacial del número de larvas y pupas a través de la cartografía

El primer paso es producir un mapa de los valores en cada barrio antes y después de la intervención utilizando una escala de representación común. Estas representaciones gráficas se describen detalladamente en varios manuales de cartografía, que permiten elegir la representación gráfica adecuada para cada tipo de variable y cada tipo de objeto geográfico (puntos, líneas, superficies) (Bertin 1967; Bailly 1992).

Se pueden utilizar varios programas de software, de pago (ArcGIs o Mapinfo) o libres (QGIs), para trazar un mapa del número de larvas y pupas utilizando un tamaño de punto proporcional al número. Es necesario disponer de las coordenadas geográficas de cada hogar en el que se haya realizado el estudio entomológico y para el que se haya calculado un número total de larvas y pupas. Por ello, a fin de evitar el sesgo de interpretación, es necesario un diseño de muestreo espacial (muestreo aleatorio en el espacio) para la recolección entomológica.

Los mapas (Figura 1) representan todos los hogares en los que se recogieron datos. Si no se han encontrado larvas, el hogar está representado por un punto azul en el mapa; no expresa ninguna cantidad. Para los demás hogares, el punto negro representado es gráficamente proporcional al número de larvas y pupas calculado. La comparación de los mapas permite observar varios fenómenos.

Durante la fase inicial, antes de la intervención, se observa un número importante de larvas y pupas en las zonas de intervención y control. En cada una de estas zonas aparecen zonas con un mayor número de larvas y pupas que en otras partes de los barrios. Esto ilustra que las larvas de Aedes aegypti están presentes en todas partes de Uagadugú y que hay, por múltiples razones, “bolsas” en las que estas larvas son más numerosas.

Durante el último análisis posterior a la intervención, se observó una disminución significativa del número de hogares con alojamientos de larvas y pupas en Tampouy, la zona de intervención. En el sector de control, Juvenat, que no fue objeto de intervención, se observa que los depósitos identificados durante la fase inicial están en su mayoría presentes, y la aparición de nuevos depósitos. Cabe señalar que los efectos no se asocian con una menor precipitación en una zona en comparación con otra, y de un año a otro, y por lo tanto con una menor productividad de los depósitos larvarios.

Este primer paso es sencillo de llevar a cabo; proporciona una representación cartográfica del fenómeno. Sin embargo, para caracterizar los “bolsillos” y medir si existe una concentración del número de sitios de cría y larvas en ciertas partes de los barrios y cómo ha evolucionado después de la intervención, se deben hacer mediciones globales y luego locales de los valores asociados a los hogares.

Fase 2: Medición de la distribución espacial del número de larvas y pupas en las zonas de estudio de Uagadugú

En esta fase se mide la autocorrelación espacial para determinar si existe una correlación entre el valor de los objetos y las relaciones métricas o topológicas entre ellos. Los índices de correlación se utilizan para dar cuenta de los valores vecinos, el más utilizado de los cuales es el índice de Moran. Se define como el promedio de los productos de los valores normalizados de los pares de puntos, ponderados por la distancia entre los dos puntos (Moran, 1948).

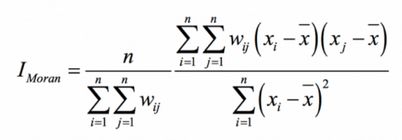
Donde ij= unidad espacial; n=numero de unidades espaciales; x_i es el valor de la variable en la unidad i; x es la media de x̄; y w_ij son los elementos de la matriz de interacciones espaciales, definida como la cercanía, las distancias o las fronteras comunes.

Por consiguiente, este índice mide la medida en que, para la totalidad de la muestra, el valor de los individuos se aproxima o se aleja del de su vecindario en relación con la media. Esta medida es global (Cliff, 1969) ya que se relaciona con la similitud de los lugares con su vecindario para toda la muestra. En el caso de esta evaluación, el índice de Moran indica si las viviendas de los hogares con un número significativo de larvas y pupas están cerca o lejos, lo que revela una autocorrelación espacial positiva o negativa. Este es el primer paso antes de intentar investigar más a fondo la ubicación de los agregados.

El valor del índice de Moran en el barrio de Tampouy antes de la intervención muestra una autocorrelación espacial positiva (si el índice es superior a cero), relativamente baja (i=0,10), pero con una dispersión de los valores del índice que sugiere que los agregados pueden estar presentes. Tras la intervención, observamos que la autocorrelación espacial es cero (i=-0,02), lo que significa que los valores están distribuidos aleatoriamente, sin autocorrelación, y muestra una evolución entre las dos fases de recogida y por lo tanto un efecto de la intervención. En el sector de control, la autocorrelación espacial global es también positiva (i=0,05) antes de la intervención y nula (i=-0,004) después. Por lo tanto, la evolución general en los dos barrios es similar. Sin embargo, es importante verificar la evolución a nivel local, es decir, a nivel de la vivienda, en particular para comprobar si hay agregados y, en caso afirmativo, cómo han evolucionado.

Fase 3: Indicadores locales de la asociación espacial del número de larvas y pupas en los barrios

Los indicadores de asociación espacial local desarrollados por Luc Anselin permiten llevar a cabo estas evaluaciones. Analizan la concentración de valores similares y disímiles medidos en un conjunto de puntos o calculados por agregación espacial.

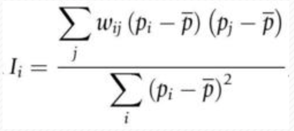
Donde p_i y p_j son los valores de las unidades espaciales i y j, de tal manera que i y j se consideran vecinos en base a la medición de su grado de proximidad, p_i es el valor medio de las unidades espaciales y w_ij una medida de la proximidad de las unidades espaciales i y j.

El procedimiento se puede llevar a cabo con el software libre Geoda (Anselin, 1995). Permite llevar a cabo todos los pasos anteriores y no requiere el uso de un sistema de información geográfica para preparar los datos que se utilizarán. Por otra parte, los resultados pueden ser exportados a GIS. Antes de analizar los indicadores locales de asociación espacial, debe definirse una matriz de pesos (una tabla que enumera todas las distancias entre todos los vecinos) que identifique a los vecinos. Los pesos de los vecinos pueden construirse de varias maneras dependiendo del tipo de objeto geográfico (un punto o una superficie). En el caso de la intervención para el control del dengue que se presenta aquí, los hogares están representados por puntos. Por lo tanto, la matriz se calcula a partir de una distancia entre los puntos.

El último paso es ejecutar el análisis LISA usando esta matriz de peso. Se calcula una estadística para cada unidad, que se basa en el valor de las unidades vecinas. El resultado son dos tipos de mapas: uno que representa los valores del índice calculado y muestra cómo varía el índice en todo el territorio, y otro que pone de relieve las relaciones estadísticamente significativas de los índices mediante la cartografía de los agregados para ilustrar las similitudes y las disimilitudes de los valores.

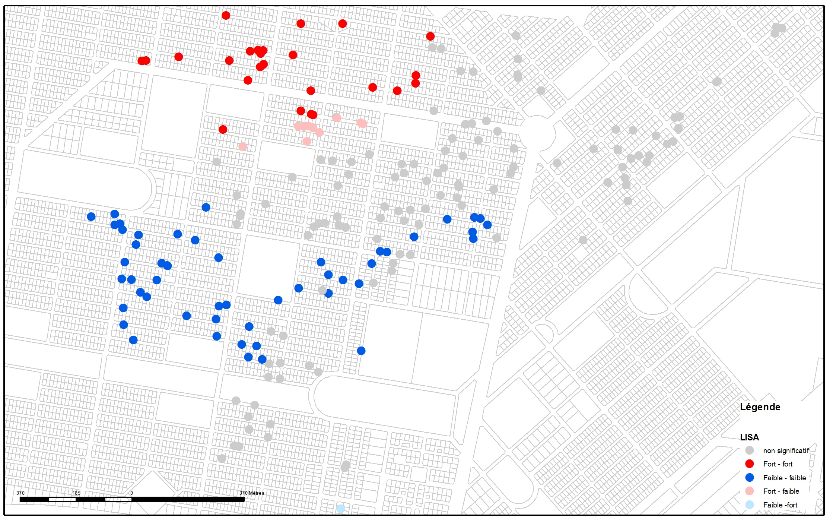
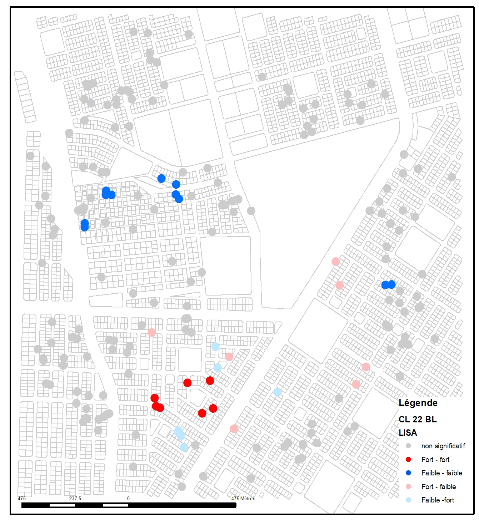
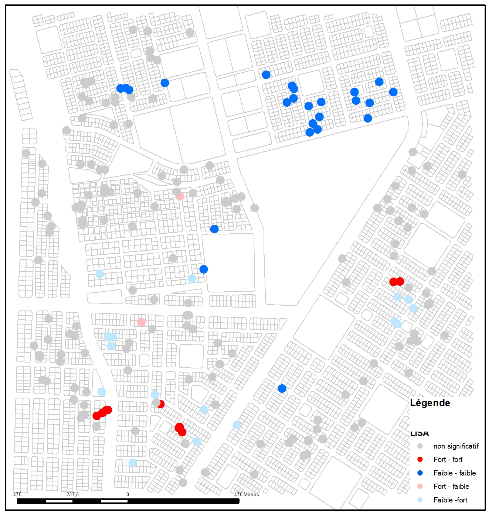
Los mapas LISA (figuras 3a, 3b, 3c y 3d) de los valores larvarios y de pupas de la zona de intervención de Tampouy (arriba) muestran que, antes de la intervención, había agregados de valores negativos (azul) y positivos (rojo). Esto significa que había dos tipos de concentraciones, ambas muy claras en el vecindario. En el azul, había una concentración de hogares que tenían hábitats de larvas y pupas relativamente improductivos porque tenían un número bajo de larvas y pupas. Esta concentración de valores bajos también significa que los hogares vecinos tenían características similares (bajo número de larvas). Por el contrario, en el norte de la zona, la concentración de valores altos está representada por los puntos clasificados como fuertes-fuertes (valores fuertes del hogar y sus vecinos). Por lo tanto, el análisis LISA muestra una doble concentración de valores opuestos de larvas y pupas. Esto no significa una presencia o ausencia de larvas y pupas, sino que había zonas graduadas de producción de larvas y pupas en el área de estudio antes de la intervención.

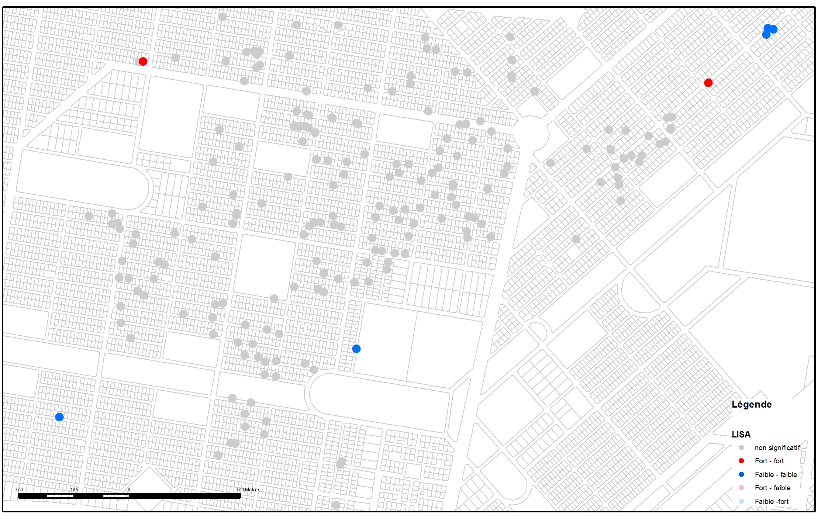
Después de la intervención, los análisis de LISA muestran pocos agregados de cualquier tipo y la desaparición de los agregados que existían antes de la intervención. Por consiguiente, el análisis muestra que la intervención dio lugar a una reducción del número de zonas con concentraciones altas y bajas de larvas y pupas. El análisis general confirma esto con una autocorrelación espacial nula, lo que significa que la presencia de larvas y pupas en la zona de intervención es ahora aleatoria. Este análisis complementa los análisis de los epidemiólogos que observaron una reducción significativa de los índices entomológicos en Tampouy después de la intervención.

En la zona de control se observaron agregados que persistieron en los mismos lugares durante la recolección posterior a la intervención y confirmaron el aumento de la producción de larvas y pupas identificado por los demás análisis epidemiológicos.

Análisis reflexivo y conclusión

La evaluación de la dimensión espacial en las intervenciones de salud pública suele limitarse a un análisis de los efectos medios de la intervención que varían según las características geográficas y las medidas aproximadas de la distancia. Los métodos tradicionales utilizados para la evaluación no captan la variabilidad espacial de los lugares y los efectos de las intervenciones. El método utilizado en el presente capítulo es un ejemplo de análisis espacial que puede utilizarse. Estos métodos se utilizan rara vez para evaluar las intervenciones y más a menudo para explorar la propagación espacial o la concentración de una enfermedad. Sin embargo, este ejemplo demuestra que los fenómenos pueden observarse a diferentes escalas y que los resultados globales pueden ocultar diferentes situaciones locales. La dimensión espacial de estos análisis complementa otros resultados en el contexto de la evaluación del impacto de una intervención. Por consiguiente, se recomienda generalizar el uso de análisis espaciales en la evaluación de las intervenciones a fin de aprehender todos los efectos a todas las escalas.

En el ejemplo presentado, el procedimiento utilizado demostró ser eficaz y no planteó ninguna dificultad siempre que la toma de muestras fuera geográfica. Este es uno de los puntos fundamentales de los métodos de análisis espacial. La calidad de los resultados depende de un plan de muestreo geográfico que asegure la correcta interpretación de los resultados. Uno de los retos de este método es encontrar los hogares en la fase posterior a la intervención. En los países en que no existen direcciones de calles, es necesario utilizar el GPS y asegurarse de que la geolocalización es correcta y está bien registrada. En entornos urbanos densos, algunas perturbaciones de la señal interfieren con las posiciones registradas en el GPS y hacen más difícil encontrar los hogares encuestados en la fase previa a la intervención. Al realizar encuestas de población, asegúrese de registrar el número de teléfono del encuestado para que sirva como una forma alternativa de localizar el hogar. La falta de rastreo del hogar de la encuesta original es la principal debilidad del método en lo que respecta a su aplicación en los países de ingresos más bajos. Otras deficiencias se refieren al propio método, que permite el análisis de una sola variable a la vez, lo que limita la inclusión de otras variables que pueden considerarse confusas. Sin embargo, hay otros métodos geográficos que combinan varias variables y serían complementarios (regresiones de GWR ponderadas geográficamente) de las evaluaciones estadísticas.

El acceso a estos métodos se facilita hoy en día por la disponibilidad de software gratuito de Sistemas de Información Geográfica como QGIS. Permiten cartografiar la geolocalización de los hogares en una encuesta, pero también realizar muestreos geográficos. Asociado a las herramientas libres “GeoDa” desarrolladas por Luc Anselin, también se facilita la realización de LISA.

Referencias

Anselin, L., (1995). Local indicators of spatial association – LISA. Geographical Analysis, 27(2), 93-115.

Bailly A. S. (1999). Pumain D. et Saint-Julien T., L’analyse spatiale T. 1. Annales de Géographie, (605), 105.

Bertin, J. (1967). La sémiologie graphique : les diagrammes, les réseaux, les cartes. La Haye ou Paris : Mouton ou Gauthier-Villars.

Caloz, R. et Collet, C. (2011). Analyse spatiale de l’information géographique (1^e éd.). Lausanne : Presses polytechniques et universitaires romandes

Cliff, A. D. et Ord, K. J. (1969). The problem of spatial autocorrelation. Dans A. J. Scott (dir.), Papers in Regional Science, Studies in Regional Science (vol. 1, p. 25-55). Londres: Pion.

Moran, P. A. (1948). The interpretation of statistical maps. Journal of the Royal Statistical Society: Series B, 10(2), 243-251.

Observatoire des populations de Ouagadougou, Projet Wellcome Trust 2008-2013. (2013). Rapport scientifique sur la caractérisation sociologique des quartiers de l’OPO.
http://www.issp02.issp.bf/opo/Publications/Rapport-scientifique-juin2013-Caracterisation-des-quartiers-Axe-qualite.pdf

Oliveau, S. (2010). Autocorrélation spatiale : leçons du changement d’échelle. L’Espace Géographique, 39(1), 51-64.

Resumen / Résumé / Abstract

Este capítulo presenta un análisis espacial de una intervención para evaluar si los valores similares de un resultado tienen más probabilidades de formar grupos en un área de estudio. Este método, denominado “indicadores locales de asociación espacial” (LISA), identifica áreas en las que los valores dependen espacialmente unos de otros. LISA se utilizó para evaluar el impacto de una intervención comunitaria para controlar al mosquito responsable de la propagación del dengue Aedes aegypti en dos barrios de Uagadugú, la capital de Burkina Faso. La evaluación final de la intervención utilizando este método mostró que los grupos de larvas desaparecieron en el área que recibió la intervención mientras persistían en el área de control.

***

Ce chapitre présente une analyse spatiale d’une intervention qui vise à évaluer si des valeurs similaires d’un résultat sont plus susceptibles de former des grappes dans une zone d’étude. Cette méthode appelée « indicateurs locaux d’association spatiale » (local indicators of spatial association – LISA) permet d’identifier les zones où les valeurs sont spatialement dépendantes les unes des autres. LISA a été utilisé pour évaluer l’effet d’une intervention communautaire visant à contrôler le moustique responsable de la propagation de la dengue Aedes aegypti dans deux quartiers de Ouagadougou, capitale du Burkina Faso. L’évaluation finale de l’intervention à l’aide de cette méthode a montré que les groupes de larves ont disparu dans le quartier qui a reçu l’intervention alors qu’ils persistaient dans le quartier témoin.

***

This chapter present a spatial analysis of an intervention which aims at assessing whether similar values of an outcome are more likely to form clusters in a study area. This method called local indicators of spatial association (LISA) enable to identify areas where values are spatialy dependant with one another. LISA has been used to evaluate the effect of a community-based intervention which aims at controlling the mosquito responsable for spreading Dengue, Aedes aegypti in two neighborhoods of Ouagadougou the capital city of Burkina Faso. The final evalutation of the intervention using this method showed that larva clusters disappeared in the neighborhood which received the intervention while they persisted in the control neighborhood.

***

Emmanuel Bonnet es geógrafo de la salud e investigador del IRD (Institut de Recherche pour le Développement). Ha realizado muchas investigaciones en el África occidental y tiene experiencia internacional en los ámbitos de vigilancia de epidemias, tecnologías geomáticas, sistemas de información geográfica y el análisis espacial.

Samiratou Ouédraogo es epidemióloga e investigadora de salud pública con experiencia internacional en evaluación. Trabaja en numerosos proyectos de investigación en Canadá y África.

Diane Saré es médico de salud pública. Tiene experiencia profesional clínica comunitaria y hospitalaria. También tiene experiencia en la aplicación y evaluación de intervenciones comunitarias.

Cita

Emmanuel Bonnet, Samiratou Ouédraogo y Diane Saré (2020). Análisis espacial. Un caso de intervención comunitaria para controlar el mosquito Aedes aegypti en Burkina Faso. En Evaluación de las intervenciones sanitarias en salud global. Métodos avanzados. Bajo la dirección de Valéry Ridde y Christian Dagenais, pp. 347-364. Québec: Éditions science et bien commun y Marseille: IRD Éditions